This subsubtopic focuses on determining unknown parameters in exponential differential-equation models by interpreting contextual data, ensuring students can accurately connect observed values to the form of an exponential solution.

Using Data to Determine Parameters in Exponential Models

A differential equation of the form $\frac{dy}{dt} = ky$ describes exponential behavior, meaning the rate of change of a quantity is proportional to its current amount. Solving this differential equation produces a general exponential model that allows AP Calculus AB students to use real-world data to determine unknown constants and fully specify the model for a given situation.

When working with exponential models, AP students must identify how numerical data—such as initial values or additional observed points—allow us to solve for the constants that define the solution curve. These constants typically include the initial amount and the growth or decay constant, both of which give the model its specific shape and behavior over time.

Understanding the Exponential Model Form

The standard exponential solution derived from $\frac{dy}{dt} = ky$ is written as $y = y_{0}e^{kt}$, where constants must be determined from contextual information.

This formula expresses how a quantity evolves exponentially and provides the structure needed to incorporate given data.

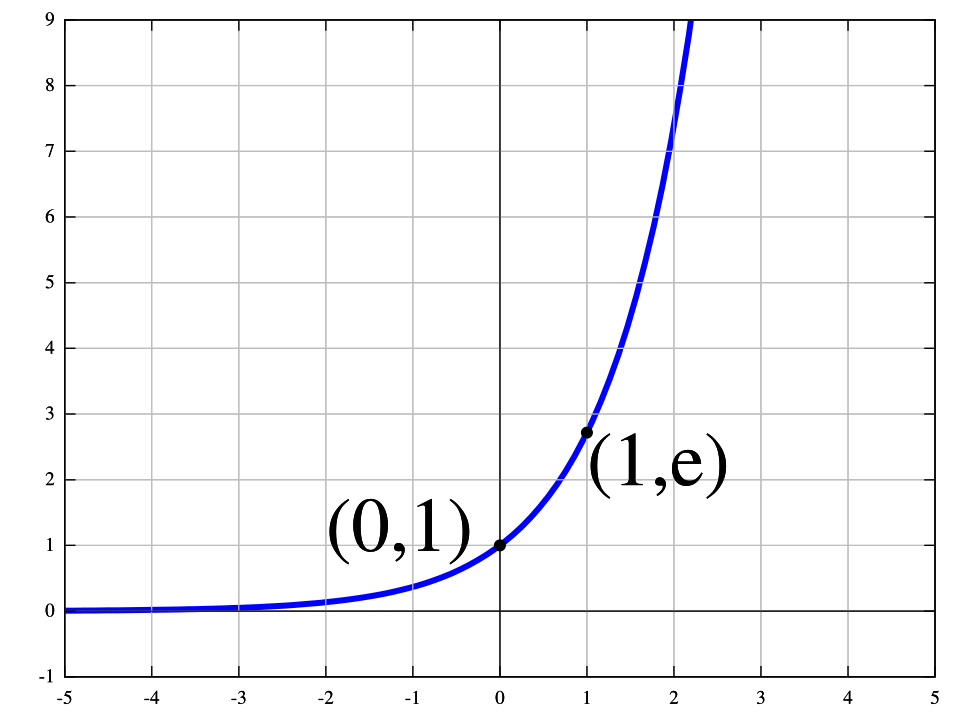
This graph shows the natural exponential function $y = e^{x}$ on the interval −5 to 5, illustrating the characteristic shape of exponential growth. It reinforces the structure of the model $y(t)=y_{0}e^{kt}$ when $y_{0}=1$. The image contains only core graph features relevant to AP Calculus AB. Source.

A sentence here to maintain spacing before any additional definitions.

Identifying Known and Unknown Parameters

Students often encounter exponential models where either $y_{0}$, $k$, or both are unknown. To determine these constants, the model must be paired with contextual data, such as:

• An initial condition

• A value of the quantity at a later time

• Multiple measured data points

• Descriptions indicating growth or decay behavior

When the initial condition is explicit, determining $y_{0}$ is straightforward. Additional data, such as another point on the function, then allow for determining $k$.

Interpreting Initial Conditions

An initial condition is information that specifies the value of the function at a particular time. It is most commonly expressed as a statement like “when $t = 0$, the quantity is $y_{0}$.”

Initial conditions anchor the model at a specific point, ensuring the mathematical equation aligns with observed or given starting information.

A sentence here to separate definition and upcoming content.

Using Additional Data Points to Determine Constants

When only one condition such as $y(0) = y_{0}$ is available, the parameter $k$ remains unknown. To find $k$, students use an additional data point, meaning another pair of values $(t, y)$ from the situation. The exponential model must satisfy this second condition, allowing the unknown constant to be computed algebraically.

To determine parameters using data, students typically follow this process:

• Identify all known quantities from the context.

• Substitute known values into the exponential model.

• Use an additional data point to produce an equation in the unknown parameter.

• Solve algebraically for $k$ or $y_{0}$ as needed.

• Rewrite the model with the determined constant(s) to produce a complete exponential solution.

These steps ensure that the model fits the provided measurements and reflects the real-world behavior described.

Connecting Parameter Values to Model Behavior

Once constants such as $y_{0}$ and $k$ are determined, students must understand how these values shape the solution curve. The constant $y_{0}$ determines where the graph begins, while $k$ governs the model’s growth or decay. Specifically:

• If k > 0 , the model represents exponential growth.

• If k < 0 , the model represents exponential decay.

• The magnitude of $k$ influences how quickly the quantity increases or decreases.

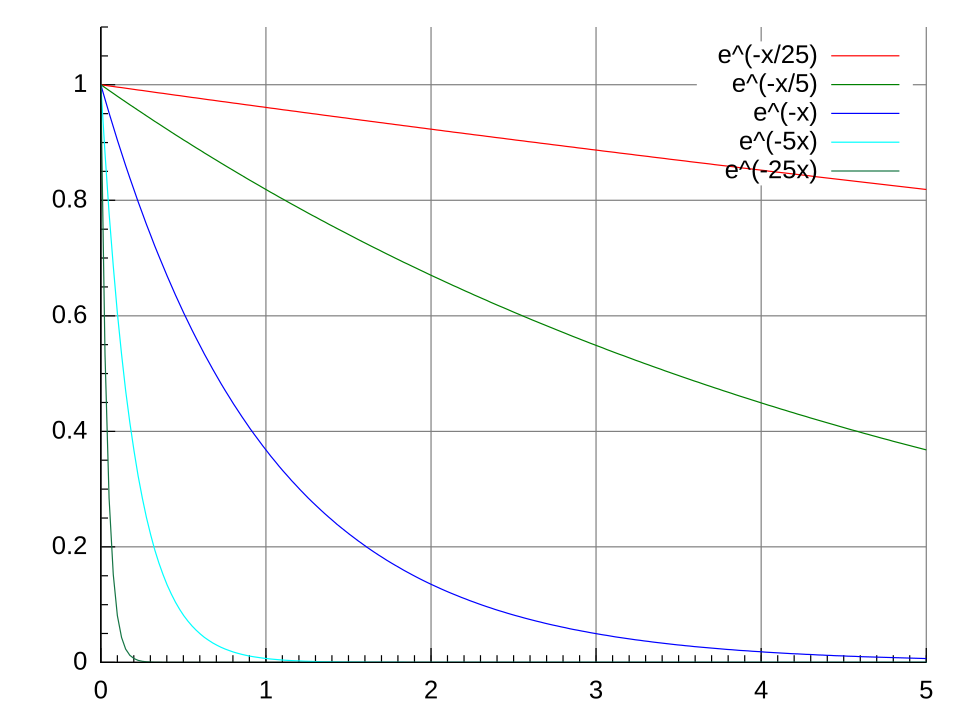
This diagram shows multiple exponential decay functions, highlighting how different values of the constant $k$ affect the rate at which the quantity decreases. It illustrates that more negative $k$ values produce faster decay. The presence of multiple curves adds comparison detail but remains aligned with understanding parameter effects in exponential models. Source.

Knowing the effect of $k$ is essential because many contextual problems emphasize interpreting model behavior once parameters have been found.

Importance of Parameter Determination in Context

Determining parameters from data ensures that an exponential model accurately reflects the situation it describes. Students must not only compute constants but also interpret them meaningfully. For example, $y_{0}$ always represents the “starting value” of the quantity, and $k$ measures the rate at which the quantity grows or shrinks.

To find $k$, students use an additional data point, meaning another pair of values $(t, y)$ from the situation.

This scatter plot illustrates how real-world data often appear as discrete points rather than a continuous curve. Such measured values at different times could be used to determine parameters like $y_{0}$ and $k$ in an exponential model. The image is generic and not tied to a specific exponential function, adding slight extra detail beyond the syllabus. Source.

This subsubtopic reinforces the connection between differential equations, exponential solution forms, and real-world modeling. By learning how to extract parameters from provided data points, students build the skill of aligning mathematical expressions with the behaviors they represent.