Applying Exponential Models to Real-World Contexts

Exponential differential equations model quantities whose rate of change is proportional to their current value, allowing students to interpret growth or decay across diverse real-world situations.

Understanding Exponential Modeling in Context

Real-world systems often change at a rate dependent on their present amount, making exponential models central to interpreting natural, physical, and social processes. When a situation states that a quantity grows or decays proportionally to its size, it is modeled by a first-order differential equation of the form $\frac{dy}{dt} = ky$. This structure links the behavior of the dependent variable to the constant rate factor that governs growth or decay.

Because proportional change is common in nature, exponential models appear in multiple AP-required contexts, including population growth, radioactive decay, and motion along a line. Each context interprets the variables uniquely but relies on the same mathematical framework.

General Solutions in Real-World Modeling

Solving an exponential differential equation provides a family of functions representing all possible behaviors consistent with the model. For $\frac{dy}{dt} = ky$, the general solution takes the form $y = Ce^{kt}$, where $C$ is an arbitrary constant representing initial size.

This general solution forms the basis for interpreting particular solutions once additional information is supplied. In applied settings, the meaning of each parameter must be tied directly to the scenario.

A sentence of normal text ensures conceptual continuity before introducing additional structured details.

For an exponential model satisfying $\frac{dy}{dt} = ky$, the general solution $y(t) = Ce^{kt}$ contains the arbitrary constant $C$, representing all functions whose graphs have the same shape but may start at different values.

A set of exponential function graphs illustrating how changing parameters produces different growth curves. Each curve has the form $y = a^{x}$, all passing through $(0,1)$ but increasing at different rates. The image includes specific functions beyond the AP syllabus but remains consistent with families of exponential solutions. Source.

Interpreting Particular Solutions in Context

A particular solution arises when the model includes enough information—usually an initial condition—to determine a unique function. In applications, interpreting the solution requires understanding:

• what the dependent variable represents

• what time $t$ measures

• the meaning and units of $C$ and $k$

• whether the situation describes growth ( k>0 ) or decay ( k<0 )

Interpreting these components helps translate the mathematical formula into statements about real-world behavior. A particular solution describes exactly how the modeled quantity evolves over time for the given scenario, rather than the full family of possible behaviors.

Population Growth as an Exponential Application

When modeling population growth, AP Calculus AB students examine situations where a population increases proportionally to its current size. This leads to equations of the form $\frac{dP}{dt} = kP$, where $P$ represents population and $k$ captures the relative growth rate. Key interpretive tasks include:

• identifying $P$ as the dependent variable and time as the independent variable

• connecting $k$ to the percentage growth rate

• understanding that $P = P_0 e^{kt}$ describes how the population evolves from the initial amount $P_0$

Population problems typically involve growth, so students interpret increasing functions and accelerating change as time progresses.

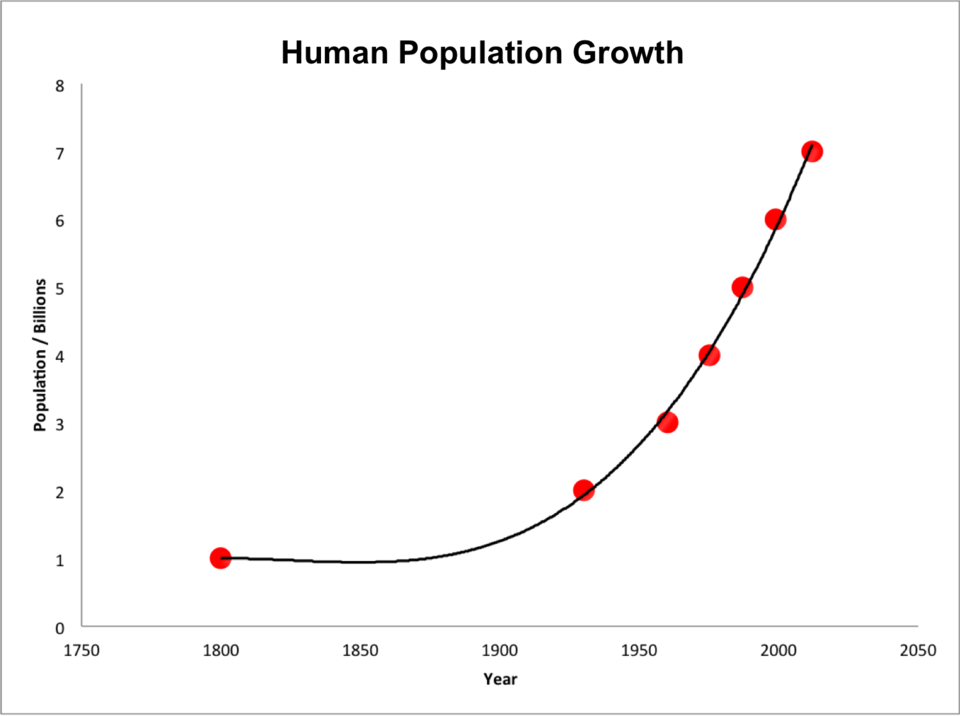
This graph shows estimated world population versus time, forming a curve that steepens dramatically in the twentieth century. Its shape is consistent with an exponential model $y = y_{0}e^{kt}$, where the rate increases with population size. Although it includes detailed historical data, this added information supports the AP goal of interpreting population growth as an exponential process. Source.

Radioactive Decay as an Exponential Application

Radioactive decay provides a contrasting example involving exponential decay rather than growth. The quantity of a radioactive substance decreases at a rate proportional to the amount present, leading to $\frac{dA}{dt} = kA$ with k<0 . Interpretive elements include:

• recognizing that the negative constant produces a decreasing exponential

• associating the model with physical behaviors such as half-life

• interpreting $A = A_0 e^{kt}$ as expressing how the amount declines over time

Students must articulate how the decay constant affects the steepness and long-term behavior of the curve, noting that the function approaches zero without ever becoming negative.

Motion Along a Line and Exponential Behavior

Some motion scenarios also rely on exponential differential equations, especially when a velocity or displacement changes proportionally to its current value. In these cases, students analyze:

• what physical quantity corresponds to the dependent variable

• how proportionality influences acceleration or velocity

• the meaning of parameters once rewritten in exponential form

These interpretations help connect calculus concepts to physical reasoning about motion.

Interpreting the Meaning of Parameters

Across all real-world contexts, the parameters in an exponential solution carry specific meanings:

• $C$ represents the initial state of the system.

• $k$ determines long-term behavior; its sign indicates growth or decay, while its magnitude affects how rapidly change occurs.

• $t$ is the independent variable marking the progression of the modeled process.

Students must clearly distinguish between mathematical structure and contextual meaning to draw correct conclusions.

Using Models to Understand Real-World Change

Applying exponential differential equations in real-world contexts requires students to articulate how the formula, constants, and derivative expression describe the behavior of the modeled quantity. Whether examining population expansion, radioactive decay, or motion along a line, the focus is on interpreting the general solution $y = Ce^{kt}$ and explaining how a given particular solution fits the situation described by the initial information.