Understanding whether an exponential model represents growth or decay is essential for interpreting real-world behavior, as the constant k fundamentally determines how solutions evolve over increasing values of the independent variable.

Growth versus Decay in Exponential Differential Equations

In an exponential differential equation of the form $\frac{dy}{dt} = ky$, the constant k governs how the dependent variable changes with respect to time. Because this relationship directly ties the rate of change to the current amount, the solution displays predictable long-term behavior based on the sign and magnitude of k.

The Role of the Constant k

The value of k serves as the determining factor for whether the model represents exponential growth or exponential decay. When first analyzing such equations, students should focus on both the sign and the relative size of k, as each affects solution behavior differently.
Students analyze exponential models by considering the sign and size of the constant k, distinguishing between growth and decay and describing how solutions behave as time increases.

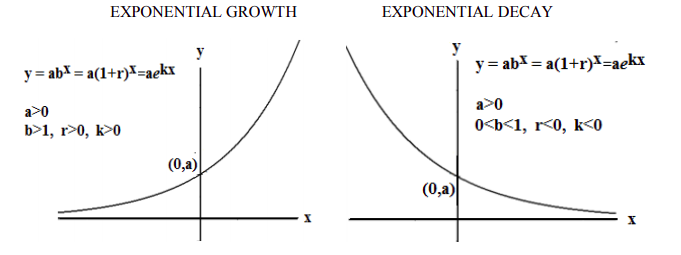
This figure compares exponential growth and decay curves, each beginning at the same initial value. Growth corresponds to parameters such as k>0, while decay corresponds to k<0. The labels $a$, $b$, and $r$ provide standard exponential notation that extends slightly beyond this subsubtopic but remains appropriate for AP Calculus AB. Source.

A sentence explaining follows: When the rate of change is positive and proportional to the quantity, the function accelerates upward over time, causing increasingly rapid growth.

After introducing decay, it is important to note that negative values of k produce functions that approach zero without ever becoming negative, reflecting many natural diminishing processes.

Solution Form and Behavior Over Time

Both growth and decay share the same general solution structure. Once students understand how the exponential solution behaves, they can identify long-term trends directly from the differential equation without needing to compute additional values.

Although the equation itself is compact, its behavior changes dramatically depending on the characteristics of k, making interpretation essential for AP Calculus AB students.

Interpreting Growth Behavior When k > 0

When k > 0, the graph of y = y₀e^{kt} shows exponential growth: it passes through (0, y₀), increases monotonically, and remains concave up for all relevant values of the independent variable.

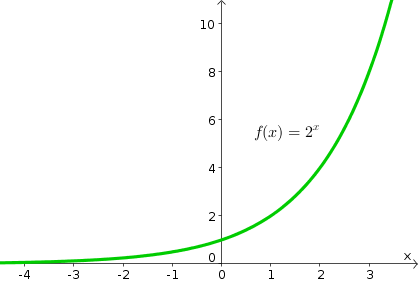
This graph illustrates the exponential function $y=2^x$, demonstrating continuous, accelerating growth. The curve increases more rapidly as $x$ increases and approaches the horizontal asymptote $y=0$ for negative $x$. Its concave-up shape and monotonic increase reflect the behavior expected when k>0. Source.

When k is positive, the function rises increasingly quickly. The slope field associated with $\frac{dy}{dt} = ky$ will display steeper positive slopes as $y$ increases, indicating acceleration. Important features of exponential growth include:

• Continuous increase: The function consistently increases for all $t$, provided y_0 > 0.

• Increasing slope: Because the slope is proportional to $y$, larger values of the function produce steeper tangent lines.

• Unbounded growth: As $t$ increases, $y(t)$ grows without bound, reflecting many real-world models such as unrestricted population growth or compound interest.

• Sensitivity to k: Larger positive values of k cause the function to grow faster, making even small differences in k significant over time.

Interpreting Decay Behavior When k < 0

When k < 0, the graph of y = y₀e^{kt} shows exponential decay, decreasing from its initial value while remaining above the horizontal axis and flattening toward y = 0 as time increases.

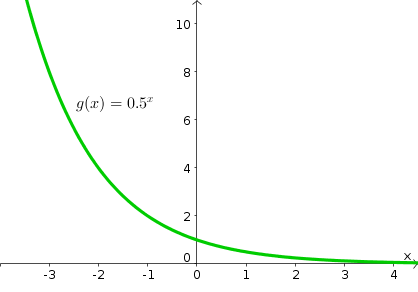
This graph shows the decay function $y=(1/2)^x$, which decreases while remaining positive. The curve approaches $y=0$ asymptotically, flattening as $x$ increases. Its shape reflects the qualitative behavior of solutions when k&lt;0. Source.

When k is negative, the function decreases at a rate proportional to its current value. The slope field will show negative slopes that flatten as $y$ approaches zero. Key features of exponential decay include:

• Continuous decrease: The function declines smoothly over time when y_0 &gt; 0.

• Decreasing magnitude of slope: Tangent lines become less steep as $y$ diminishes, showing that decay slows.

• Asymptotic behavior: The function approaches $0$ as $t \to \infty$ but never reaches it, reflecting processes such as radioactive decay or cooling.

• Sensitivity to k: Larger negative magnitudes of k result in faster decay, causing the function to decrease more rapidly.

Comparing Growth and Decay Graphs

Students should develop an ability to visualize how exponential solutions behave without computing specific values. When comparing growth and decay:

• Growth graphs curve upward, becoming increasingly steep, while decay graphs curve downward, flattening as they approach zero.

• Both types of graphs are smooth and continuous, with no sudden changes in direction.

• For the same initial value $y_0$, growth curves diverge upward, and decay curves descend toward zero, making them visually distinguishable even in a family of solutions.

Effect of the Size of k on Graph Behavior

The magnitude of k affects the rate at which the solution grows or decays:

• A larger positive k produces rapid upward acceleration.

• A smaller positive k still results in growth but more gradually.

• A larger negative k yields fast decay.

• A smaller negative k produces slow decay over a longer time span.

These distinctions allow students to infer qualitative behaviors simply by examining the differential equation.

Long-Term Behavior as Time Increases

As the syllabus emphasizes, students must describe how solutions behave as time increases:

• With k > 0, $y(t)$ accelerates upward without bound.

• With k < 0, $y(t)$ decreases toward zero.

• The graph’s long-term trend can be inferred directly from the sign of k.

Understanding these ideas enables students to interpret real-world situations modeled by exponential differential equations and to analyze solution behavior efficiently.