Logistic differential equations model situations where growth slows as a quantity nears a limiting maximum. Translating contextual statements into such equations helps represent constrained real-world growth behavior precisely.

Writing Logistic Differential Equations from Context

Logistic growth appears in systems where the rate of increase is not constant but instead depends on both the current amount and its distance from a limiting maximum. This subsubtopic focuses on interpreting verbal descriptions of constrained growth and converting them into the mathematical structure of a logistic differential equation, a core model for populations, resources, and other limited-capacity systems. AP students must reliably identify phrases signaling logistic behavior and express them using the characteristic product form of dependent-variable terms.

Recognizing Logistic Language in Context

Descriptions of logistic behavior almost always contain one or more cues about slowing growth, approaching a maximum, or limited capacity. Students should look for statements indicating that the rate of change depends simultaneously on the current quantity and on how much room remains before reaching a maximum allowable amount. Key phrasing often includes:

• “growth slows as it approaches a maximum,”

• “rate of increase decreases as the population nears its limit,”

• “restricted by available resources,”

• “self-limiting growth,”

• “approaches a carrying capacity.”

When such language appears, the underlying differential equation must resemble a product structure in which the dependent variable interacts with a term describing its unused capacity.

Dependent and Independent Variables in Logistic Contexts

In most logistic scenarios, the dependent variable is the quantity undergoing growth—often a population size, a concentration, or an amount of a substance—while the independent variable is typically time. Because logistic descriptions emphasize dynamic change, identifying these roles ensures that the correct derivative expression supports the logistic interpretation.

When the carrying capacity is specified or implied, it becomes an essential parameter in the logistic equation’s structure. This maximum is not merely a boundary; it directly shapes the functional form of the rate of change.

A verbal description connecting growth limitations to a physical, biological, or environmental constraint must therefore be interpreted as establishing a carrying capacity within the model.

Structure of a Logistic Differential Equation

A logistic differential equation takes the form of a product involving the current value of the quantity and a remaining-capacity term. This aligns with contextual descriptions in which growth occurs only when both the quantity exists and unused capacity remains. The standard logistic structure is based on a proportionality constant and two interactive factors.

This equation aligns directly with the syllabus specification: “growth that slows as a population approaches a maximum” is encoded mathematically by the factor $(a - y)$, which becomes smaller as $y$ nears the carrying capacity. The structure also ensures that when the quantity is near zero, the rate of increase is small, and when halfway to the carrying capacity, the growth rate is highest—reflecting the intuitive behavior described in logistic contexts.

Between the dependency on current size and the limiting factor, logistic models capture nonconstant change effectively in a wide range of applied scenarios.

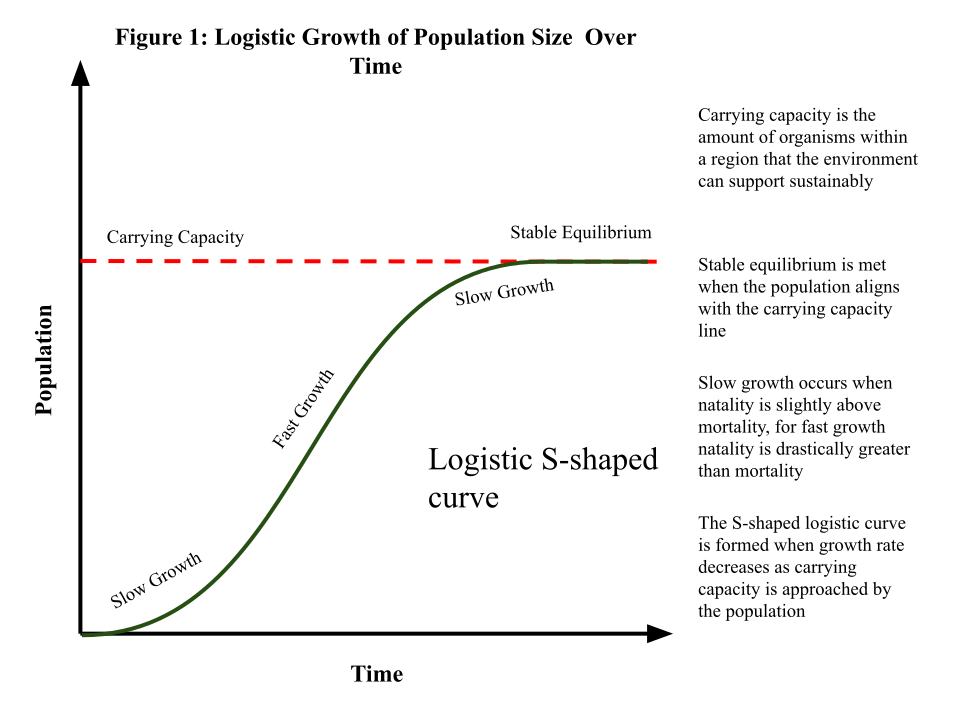
This figure shows a classic S-shaped logistic curve approaching a horizontal carrying-capacity line. The vertical axis represents population size while the horizontal axis represents time. Minor ecological labels included in the image extend slightly beyond the AP focus but help contextualize the logistic model. Source.

Translating Verbal Descriptions into the Logistic Form

To write logistic differential equations from context, students must extract mathematical meaning from qualitative statements. Use the following structured procedure:

• Identify the dependent variable (the quantity that grows) and the independent variable (usually time).

• Determine whether the description indicates slowing growth tied to a maximum limit. If so, this signals logistic behavior.

• Convert the idea of “growth proportional to the current amount” into the factor $y$ in the equation.

• Convert the idea of “slowing as it approaches a maximum” into the factor $(a - y)$, where $a$ represents the carrying capacity.

• Introduce a positive constant $k$ to represent the proportionality described in the context.

• Combine the components into the product form $dy/dt = k y (a - y)$, adjusting notation as needed to match variables used in the description.

This process requires interpreting each descriptive phrase for its mathematical implications, ensuring that structural meaning is preserved accurately.

Interpreting Parameters within Context

The carrying capacity and proportionality constant should always be linked back to the narrative description. The parameter $a$ represents the maximum level attainable given the stated limitations—such as available resources, maximum population the environment can sustain, or an upper bound determined by physical constraints. The constant $k$, while not always explicitly described, reflects how responsive the growth is to these constraints.

Once the logistic equation is constructed, students should reread the original context to ensure each component aligns with the described behavior. The product structure must reflect the dual dependence: the rate of change occurs because there is existing quantity and because additional capacity remains.

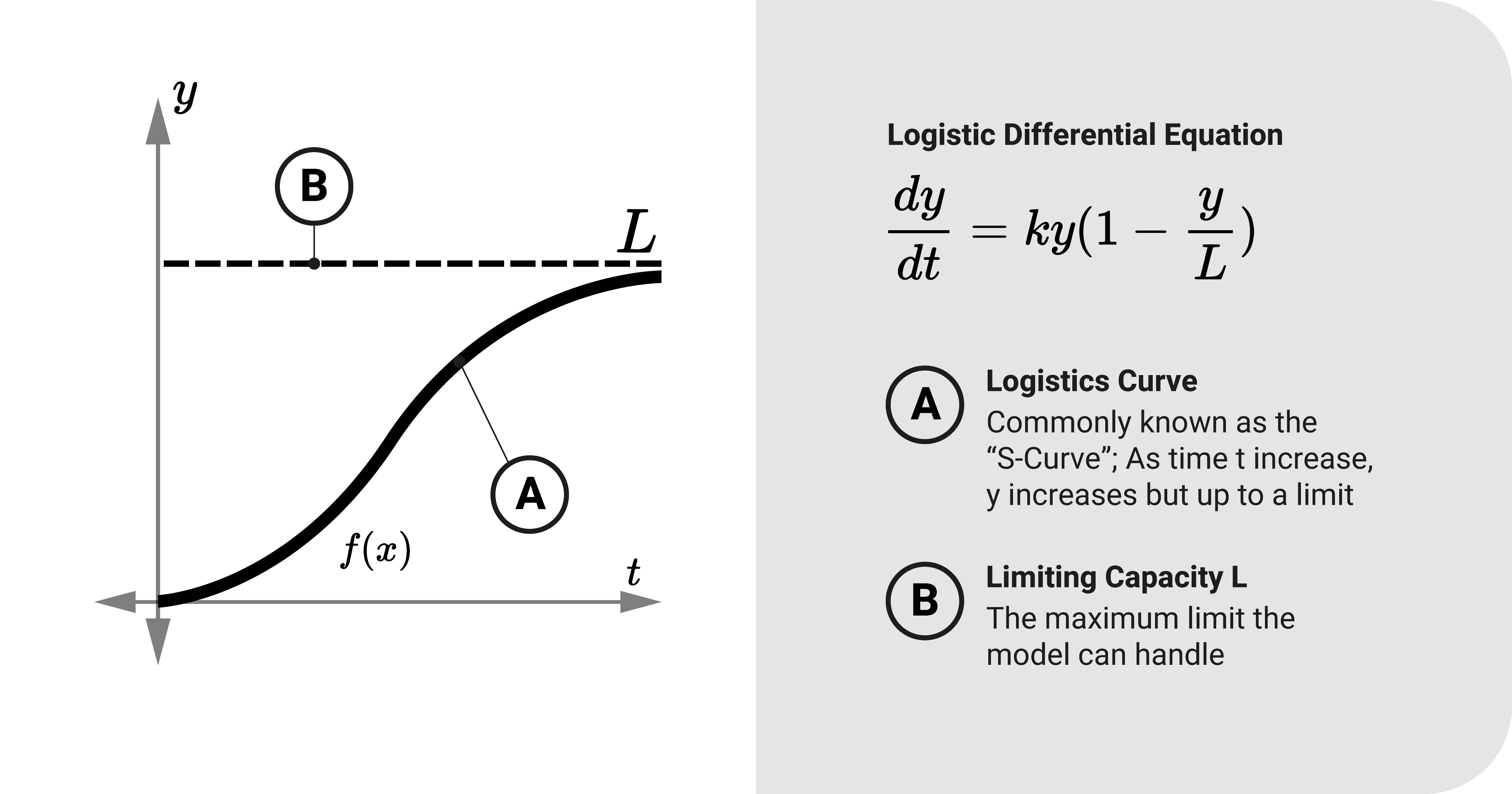
This diagram highlights the logistic differential equation $\dfrac{dy}{dt} = ky!\left(1 - \dfrac{y}{L}\right)$, linking the symbolic form to its characteristic S-curve behavior. The curve approaches a horizontal limiting value $L$, illustrating constrained growth. If present, any additional mention of the explicit solution extends slightly beyond this subsubtopic but remains conceptually consistent. Source.

Ensuring Consistency with Verbal Cues

Accurate formulation depends on recognizing that logistic language always ties growth to two simultaneous influences. When a description states that growth “slows” or “approaches” a limit, it indicates a diminishing term like $(a - y)$. When a description mentions that the rate of change is strengthened by current population or amount, it indicates a factor like $y$. Only the product of these two ideas authentically captures the logistic mechanism conveyed in the syllabus focus.