Understanding where a logistic model grows fastest helps students interpret real-world systems with natural limits, revealing how population behavior changes as it approaches and surpasses half the carrying capacity.

Maximum Growth Rate and Inflection Point

The logistic differential equation describes constrained growth, meaning the rate of change slows as a population approaches a limiting value. In this context, the maximum growth rate and the inflection point play essential roles in understanding how a logistic solution behaves. The syllabus requires students to identify the specific value of the dependent variable where the solution increases fastest, recognize why this value marks the inflection point, and connect this point to half the carrying capacity, a distinctive feature of logistic growth.

Logistic Growth Structure

A logistic model is commonly represented by a differential equation of the form $\frac{dy}{dt} = ky(a - y)$, where the product structure shows how growth depends on both the current amount and the remaining capacity before reaching the limit. The parameter $a$ represents the carrying capacity, introduced here as the maximum sustainable value determined by environmental constraints.

This structure leads to solution curves that start slowly, speed up through the midpoint, and then slow again as they level off near the carrying capacity.

A key observation from the equation’s form is that the expression $y(a - y)$ is maximized when $y = \frac{a}{2}$, indicating intuitively that maximum growth occurs exactly halfway to the carrying capacity.

The Inflection Point and Its Meaning

In a logistic curve, the inflection point is the location where the concavity changes from upward to downward. This point marks the transition between accelerating growth and decelerating growth. Students should recognize that the inflection point coincides with the maximum growth rate, because the graph changes from bending upward (increasing steepness) to bending downward (decreasing steepness) at precisely that value.

Between zero and the carrying capacity, the logistic curve first bends upward as growth accelerates due to abundant resources, then bends downward as limitations begin to restrict growth. The inflection point therefore serves as the boundary between two fundamentally different growth behaviors.

After introducing the concept of an inflection point, it becomes easier to understand why it corresponds to the fastest increase of the dependent variable. At the inflection point, the slope of the tangent line reaches its greatest value, meaning the function’s rate of change peaks exactly there.

Analytical Identification of Maximum Growth

To determine where a logistic solution is changing fastest, students refer to the structure of the differential equation itself. Because $\frac{dy}{dt} = ky(a - y)$ is the product of two quantities that decrease symmetrically away from the midpoint, the maximum occurs where the product is largest. This leads directly to the identification of the midpoint value $y = \frac{a}{2}$.

Students should understand that this value requires no explicit solution of the differential equation itself. By analyzing the structure of the derivative, the point of maximum growth becomes evident. This reinforces the syllabus emphasis on interpreting the logistic model’s behavior without necessarily solving for an explicit function.

Between the definition block and the equation block, it is important to note that logistic models are unique in making the midpoint the most rapid stage of growth. Unlike exponential models, where the growth rate continues increasing indefinitely, logistic growth peaks early and then begins to slow inexorably.

Connecting Maximum Growth to Half the Carrying Capacity

The requirement that students relate the maximum growth rate to half the carrying capacity is a distinctive element of logistic models. The value $y = \frac{a}{2}$ represents the population level at which the competing effects of growth and limitation balance most symmetrically. When $y$ is below half the carrying capacity, the scarcity of the dependent variable limits how quickly the system can grow; when $y$ exceeds half the carrying capacity, environmental resistance plays the greater limiting role.

This connection highlights the interpretive power of logistic equations. A population at half of its carrying capacity is in its most dynamic phase, responding most rapidly to changes and experiencing the steepest ascent in its trajectory. As the dependent variable crosses this midpoint, students can visually observe the shifting concavity in the solution curve, corresponding directly to the inflection point described earlier.

Behavioral Interpretation of Maximum Growth

Understanding the logistic model’s fastest-growing point equips students to reason effectively about real-world systems in which growth cannot continue indefinitely. The inflection point marks the exact transition where natural limits begin to assert themselves. By connecting the maximum growth rate to the inflection point and the halfway mark of the carrying capacity, students gain insight into both the structure of logistic equations and the broader behavior of constrained systems.

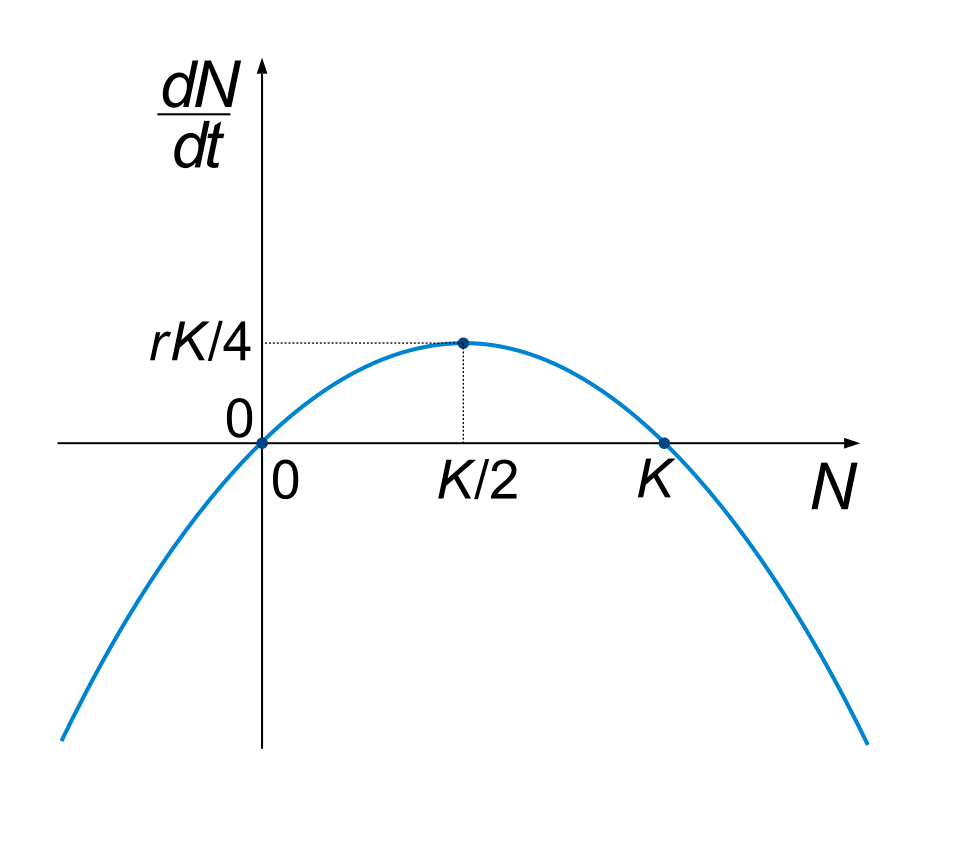
Graph of the logistic derivative $\dfrac{dN}{dt}$ forming a downward-opening parabola with zeros at $N=0$ and $N=K$, reaching its maximum at $N=\dfrac{K}{2}$, the point of maximum growth rate. Source.

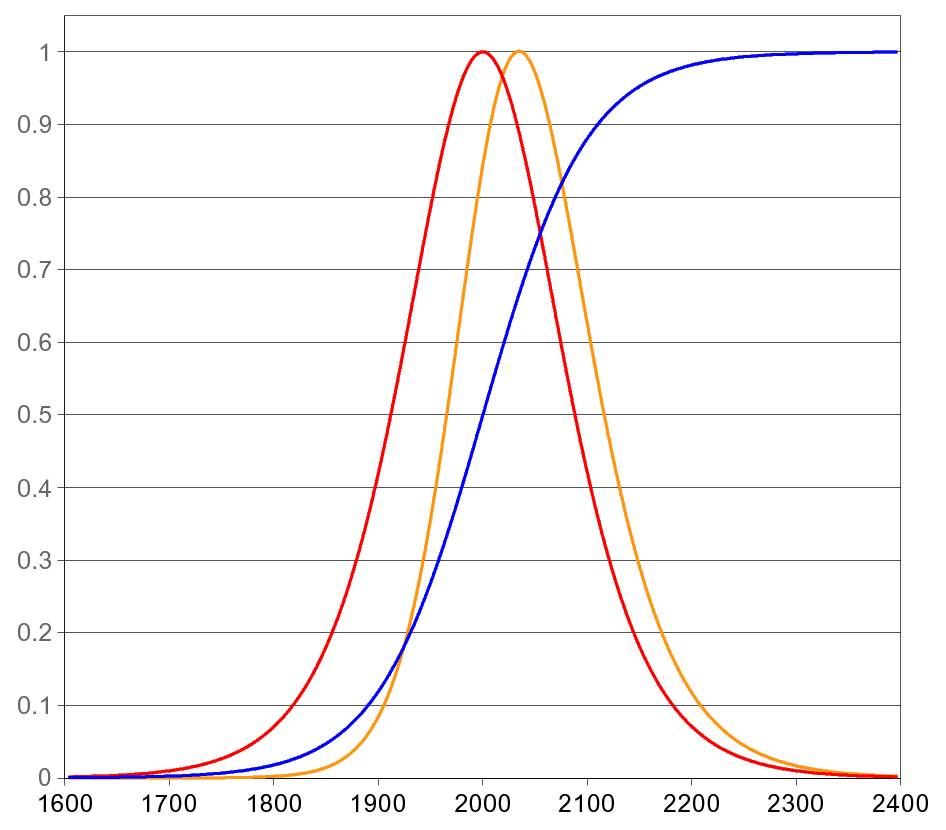
Blue curve: logistic function showing an S-shaped approach toward carrying capacity. Red curve: the growth rate $\dfrac{dy}{dt}$, rising to a single maximum at the inflection point where $y=\dfrac{K}{2}$. The orange curve includes additional weighted-growth information not required for the AP Calculus AB syllabus. Source.