Logistic differential equations describe growth that slows as a quantity approaches a limiting value. Interpreting their solutions focuses on understanding behavior over time without solving explicitly.

Understanding Logistic Differential Equations in Context

A logistic differential equation models situations where the rate of change depends both on the current amount and how close it is to a maximum sustainable level. When first introduced, the term carrying capacity requires a formal description.

A logistic equation typically appears in the form $\frac{dy}{dt} = ky(a - y)$, though exact symbols may vary. For AP Calculus AB, the emphasis is not on solving this equation but on interpreting what the structure reveals about a system’s behavior. The equation expresses that growth is proportional to both current size and remaining capacity, illustrating why growth slows as $y$ nears the upper limit.

Independent of any explicit solution formula, the logistic structure communicates qualitative features: increasing behavior when the dependent variable is small, decreasing slopes as it nears its ceiling, and an eventual leveling off toward the carrying capacity.

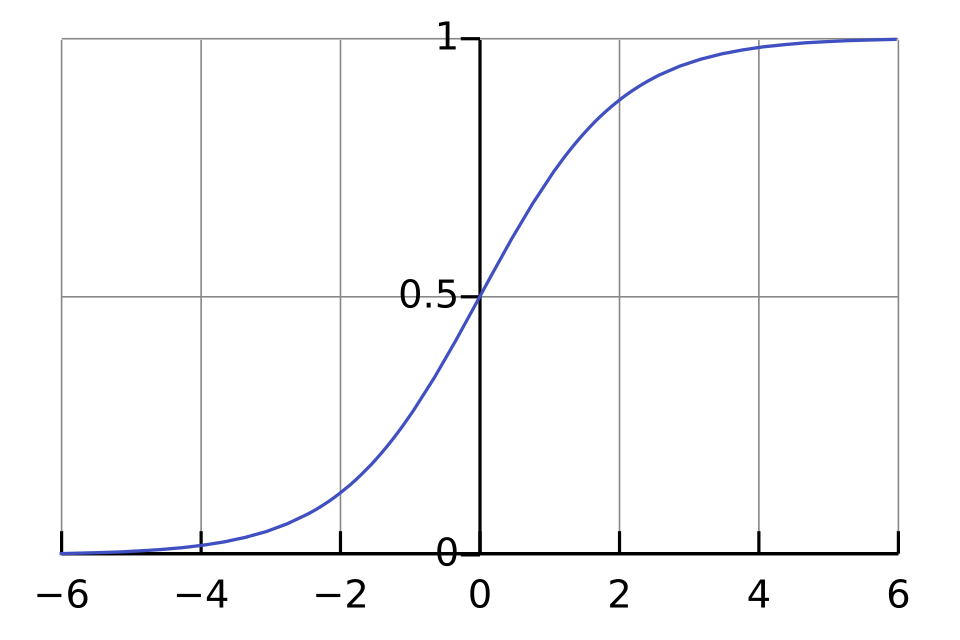
This S-shaped logistic curve illustrates slow initial growth, accelerated mid-range growth, and leveling off near a limiting value. It shows the qualitative behavior of logistic solutions without requiring an explicit formula. The normalized vertical scale adds generality beyond a specific applied context but remains consistent with the syllabus. Source.

Interpreting the Components of the Logistic Equation

The Role of Parameters and Structure

The parameter $k$ influences how quickly growth responds to current size, while $a$ sets the carrying capacity the quantity approaches over time. Logic about these parameters allows students to predict growth patterns without doing algebraic manipulation.

When interpreting logistic forms:

• If $y$ is well below $a$, then $a - y$ is large, so the rate of change is relatively high.

• As $y$ increases, the difference $a - y$ shrinks, which reduces the rate of change.

• When $y$ approaches $a$, the rate of change becomes very small, suggesting flattening behavior.

These insights help describe the solution curve’s behavior qualitatively.

Using Initial Conditions to Understand Behavior

Why Initial Conditions Matter

A logistic model includes an initial condition, a given value of the dependent variable at a specific time, which determines which member of the logistic family is used. Although no explicit solving is required here, the initial condition tells us how the system begins and influences the entire trajectory of the solution curve.

Interpreting an initial condition requires understanding its conceptual role.

Between this definition and full interpretation lies the ability to reason qualitatively from context. Students use the logistic equation and initial value to describe how fast the quantity initially changes, whether it is growing or shrinking, and how it will behave in the long term.

Qualitative Features of Logistic Solutions

Rates of Change Without Explicit Solutions

A powerful aspect of logistic modeling is predicting how the solution behaves only by studying the differential equation and slope information.

Key qualitative observations include:

• Growth is initially increasing when $y$ is small relative to the carrying capacity.

• The rate of change reaches a peak when the modeled quantity is about halfway to the carrying capacity, because both growth factors are reasonably large.

• The rate of change decreases after the midpoint, leading to slower growth as the quantity begins to saturate the environment or system.

• Long-term behavior shows leveling off, approaching the carrying capacity asymptotically.

These statements allow complete descriptions of logistic behavior without computing $y$ explicitly.

Normal descriptive reasoning applies between equation and behavior, allowing students to link slope patterns with increasing, decreasing, or stabilizing trends.

Using Slope Behavior to Interpret Logistic Trajectories

What the Slope Indicates About Growth

The logistic differential equation gives immediate information about the slope $\frac{dy}{dt}$, which describes the instantaneous rate of change. Although no equation box is required here, recognizing slope structure is essential.

Students interpret slope patterns by considering:

• Sign of $\frac{dy}{dt}$: Positive values indicate increasing behavior, which is typical for logistic models at all $y$ values below the carrying capacity.

• Magnitude of $\frac{dy}{dt}$: Larger magnitudes imply faster growth; logistic models show a rise and fall in slope magnitude as $y$ increases.

These slope ideas help students trace accurate qualitative behaviors, even when drawing or referencing slope fields.

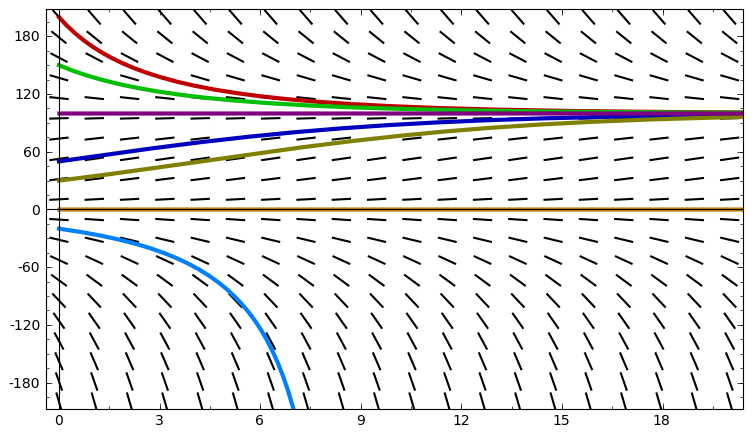
This slope field for a logistic differential equation shows how different initial conditions lead to solution curves that all approach the same carrying capacity. The heavy horizontal line represents the stable equilibrium, and the line segments show how local slopes guide each trajectory. The inclusion of negative $y$-values and specific numerical scales extends beyond the AP syllabus but does not add conceptual difficulty. Source.

Connecting Logistic Differential Equations with Real-World Interpretation

Describing Situations Without Solving

Interpreting logistic solutions often involves explaining real-world implications. Students must articulate how the modeled quantity changes over time, including:

• How initial population size affects early growth behavior.

• Why growth slows as limiting factors become more significant.

• What long-term behavior suggests about system stabilization or equilibrium.

In many contexts—population growth, spread of disease, resource-limited expansion—the logistic structure naturally captures diminishing growth due to constraints.

The emphasis in this subsubtopic is the ability to describe and reason qualitatively. Students interpret what the logistic equation and its initial condition communicate about the entire evolution of the modeled quantity without ever writing down an explicit solution formula.