The long-term behavior of logistic differential equations reveals how a quantity evolves as time progresses, emphasizing how growth slows and approaches an upper bound called the carrying capacity.

Long-Term Behavior in Logistic Growth

Logistic models arise when the rate of change of a quantity depends not only on the current amount but also on how close that amount is to a maximum sustainable level. This characteristic makes logistic behavior fundamentally different from exponential growth, which increases without bound.

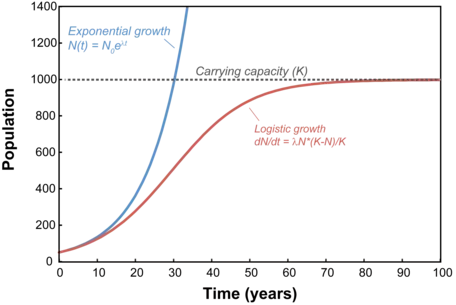
This figure contrasts an exponential curve that rises without bound with a logistic curve that bends and levels off at the dashed line labeled carrying capacity $K$. It highlights that logistic growth initially resembles exponential growth but later stabilizes at a limiting value. The image includes equations for both models, which exceed syllabus requirements but remain conceptually aligned with AP Calculus AB. Source.

In a logistic system, the interaction between growth and limiting factors shapes the eventual approach toward a stable value.

Understanding Logistic Differential Equations

The logistic differential equation typically appears in the form $\frac{dy}{dt} = ky(a - y)$, where $y$ represents the dependent variable and $t$ the independent variable. This structure encodes the idea that growth is initially fast when $y$ is small, then slows as $y$ nears a maximum threshold determined by the model. Early in the process, most solution curves rise steeply, but as the rate of increase diminishes, the graph bends and flattens toward a stable horizontal level.

The carrying capacity forms a central organizing feature of logistic behavior because it determines the upper boundary that the dependent variable cannot exceed within the mathematical model.

Behavior of Solutions as Time Increases

As $t$ increases, logistic solutions exhibit predictable qualitative tendencies. Regardless of the initial condition (as long as it is positive and below the carrying capacity), the growth curve approaches the same long-term value. This feature makes the logistic model robust for describing phenomena where constraints naturally limit continued increase, such as population saturation or resource-dependent growth.

Because the quantity $k(a - y)$ becomes small when $y$ approaches $a$, the slope of the solution curve becomes nearly horizontal. A nearly horizontal tangent line conveys that the rate of change is minimal, establishing a stable long-term value.

As the curve approaches the carrying capacity, its rate of change becomes nearly zero, and the graph approaches a horizontal line located at the carrying capacity value.

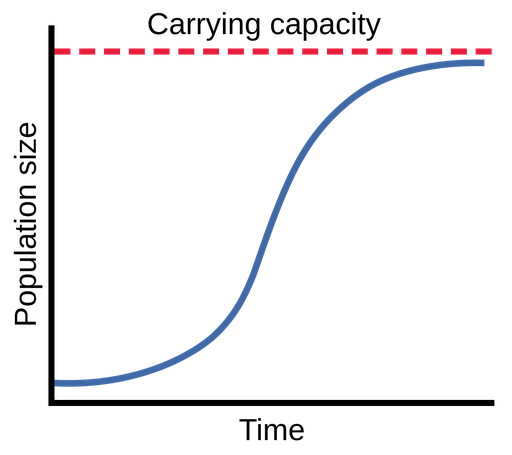
This logistic curve rises quickly at first and then gradually flattens as it approaches the red dashed carrying-capacity line. The near-horizontal behavior at the top visually represents the limiting value predicted by the logistic differential equation. Axes labels are generic so students can interpret the vertical axis as any quantity modeled logistically. Source.

Why Carrying Capacity Functions as a Limit

The carrying capacity acts like a mathematical equilibrium. If the system begins below this level, the positive rate of change drives the solution upward, but at a decreasing pace. If the dependent variable were somehow pushed slightly above the carrying capacity in a hypothetical extension of the model, the rate expression would become negative, pulling the value back downward. This regulatory behavior identifies the carrying capacity as an equilibrium solution, though the focus of this subsubtopic centers on determining and interpreting the limiting value itself.

This equilibrium function anchors the long-term behavior of all logistic solutions. In the logistic model, the equilibrium associated with growth is stable, meaning solutions nearby tend to move toward it over time.

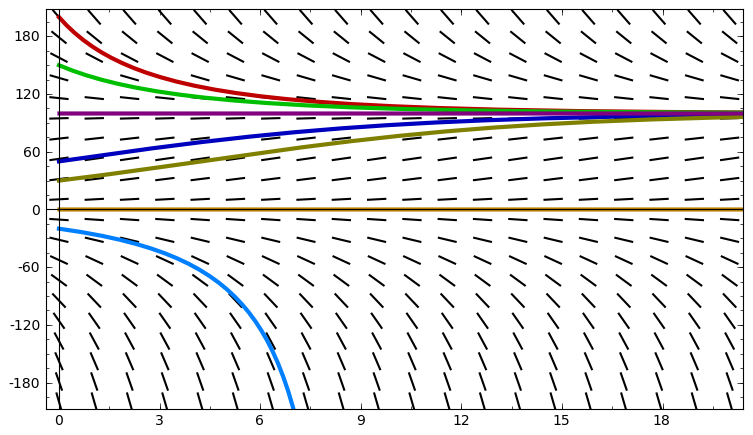
This slope field and its solution curves illustrate how all positive initial values approach the stable equilibrium line at $y=100$. The flattening of solution curves emphasizes the limiting value that logistic models predict. Negative-region behavior appears in the diagram but exceeds AP requirements; students should focus on the positive portion above the $t$-axis. Source.

Visualizing the Approach Toward the Limit

Although the subsubtopic does not require solving logistic equations explicitly, visualizing or reasoning about their shape helps clarify long-term tendencies. A logistic curve initially resembles exponential growth, rising steadily from the initial condition. Over time, however, the concavity changes as the growth rate slows. This change in concavity reflects the diminishing influence of the growth term. As the curve approaches the carrying capacity, its rate of change becomes nearly zero, and the graph approaches a horizontal line located at the carrying capacity value.

Students should recognize that the carrying capacity can be identified directly from the logistic differential equation’s structure. The value multiplying the $y$-term in the expression $(a - y)$ provides the limit toward which $y$ moves. Thus, the parameter $a$ is not merely a number in the equation but a guiding value dictating the long-term behavior of all solution curves.

Key Observations for AP Calculus AB

Understanding long-term behavior in logistic models requires recognizing that:

• Carrying capacity represents the limiting value of the dependent variable.

• Growth slows progressively as the solution nears this limit.

• The logistic differential equation contains the carrying capacity explicitly in the factor $(a - y)$.

• The slope field for a logistic equation shows horizontal segments at the carrying capacity.

• All solutions with initial values between zero and the carrying capacity approach the same long-term value.

These observations allow students to connect qualitative solution behavior with the underlying differential equation, aligning precisely with the syllabus expectation of determining the limiting value approached by logistic solutions.