Defining Accumulation Functions with Integrals (8.3.1) | AP Calculus AB Notes

AP Syllabus focus:
‘A function defined as an integral, such as F(x)=∫_a^x f(t) dt, represents the accumulation of a rate of change from a starting point a up to the input x.’

Accumulation functions help quantify how a changing quantity builds over time, allowing definite integrals to represent total change from a fixed starting point to any chosen input.

Understanding Accumulation Functions

An accumulation function is a function whose value at any input represents the accumulated effect of a rate of change from a specified starting point. In AP Calculus AB, these functions connect ideas of integration, net change, and graphical interpretation. When a rate is known or represented visually, an accumulation function captures how that rate adds up over an interval, allowing students to interpret changing quantities within a wide range of mathematical and applied contexts.

The Role of a Starting Point

Accumulation functions always begin with a fixed lower limit, often denoted by a, which anchors the measurement of change. Because integration represents the accumulation of infinitely many small contributions, choosing a starting point ensures that each value of the accumulation function corresponds to the total amount gathered from that starting value up to the current input. This structure provides a natural way to model the build-up of physical, economic, or abstract quantities that evolve over an interval.

Defining an Accumulation Function Precisely

The syllabus specifies the typical form of an accumulation function as
F(x) = ∫ₐˣ f(t) dt, where f(t) is a known rate of change.

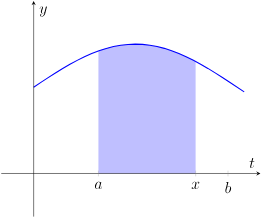
This diagram illustrates an accumulation function $F(x)$ as the signed area under the curve $y=f(t)$ from the fixed starting point $t=a$ to the variable upper limit $t=x$ . The shaded region visually represents $F(x)=\int_a^x f(t),dt$ , emphasizing that each input $x$ corresponds to a total accumulated change from $a$ to $x$ . This reflects the AP concept that an accumulation function encodes “area so far” from a lower limit up to the current input. Source.

Accumulation Function: A function whose value at $x$ equals the definite integral of a rate of change from a fixed starting point $a$ to $x$ , representing total accumulated change.

This definition highlights that accumulation functions are inherently tied to definite integrals, making them essential tools for interpreting integrals beyond basic area ideas.

Structure of the Integral Definition

The notation used in accumulation functions requires careful interpretation. The function f(t) acts as the integrand, representing a rate measured relative to the dummy variable t, which differs from the independent variable x in order to prevent ambiguity. Students should focus on understanding what quantity the integrand represents and how its accumulated effect gives meaning to the accumulation function.

$F(x) = \int_{a}^{x} f(t), dt$
$F(x)$ = Accumulated change from $a$ to $x$
$f(t)$ = Rate of change being accumulated
$a$ = Fixed starting point of accumulation
$x$ = Input at which accumulated value is evaluated

Between the structure of the integrand and the variable limits, each component contributes to the interpretation of the accumulated value.

Conceptual Interpretation of Accumulation

Accumulation functions express how a quantity builds gradually. Students should interpret these functions by imagining how the rate behaves over the interval. The integral tallies positive contributions above the axis and subtracts negative contributions below it, resulting in a comprehensive measure of net change. This process makes accumulation functions especially meaningful for quantities that fluctuate, such as velocity, growth rates, or flow rates.

Key Features of Accumulation Functions

To understand the behavior of accumulation functions, students should recognize several essential features:

They measure net change, not just total magnitude.
The sign of f(t) directly affects whether the accumulation increases or decreases.
The value F(a) = 0 when the upper and lower limits match, anchoring the function.
The graph of F(x) often smooths out short-term fluctuations in f(t).
When f(t) is continuous, the accumulation function is also continuous.

These features reinforce accumulation functions as powerful conceptual and computational tools for modeling change.

Relationship to the Fundamental Theorem of Calculus

One of the central roles of accumulation functions is their connection to the Fundamental Theorem of Calculus (FTC), which bridges differentiation and integration. While the primary focus here is definition rather than evaluation, the FTC provides context by implying that the derivative of an accumulation function reveals the original rate being integrated.

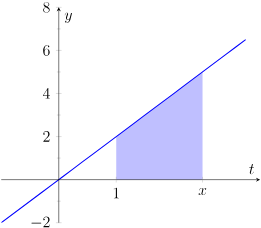
This graph compares a rate function $f(x)=2x$ with its accumulation function $F(x)=x^2-1$ , defined by $F(x)=\int_1^x 2t,dt$ . It shows how $F(x)$ grows according to the signed area under $f(t)$ and how $f(x)$ appears as the derivative of $F(x)$ , illustrating the Fundamental Theorem of Calculus. The explicit formulas extend slightly beyond the definition-focused content but reinforce that an accumulation function is an antiderivative of its integrand. Source.

This relationship enriches understanding by showing that accumulation functions are not isolated constructions but integral components of calculus’ foundational structure.

Interpreting Graphs of Accumulation Functions

Visual interpretations form a crucial part of working with accumulation functions. Students are often given graphs of f(t) and asked to reason about the behavior of F(x). When viewing a rate graph:

Positive regions of f(t) correspond to intervals where F(x) increases.
Negative regions correspond to intervals where F(x) decreases.
Areas under the curve represent exact changes in the value of the accumulation function.

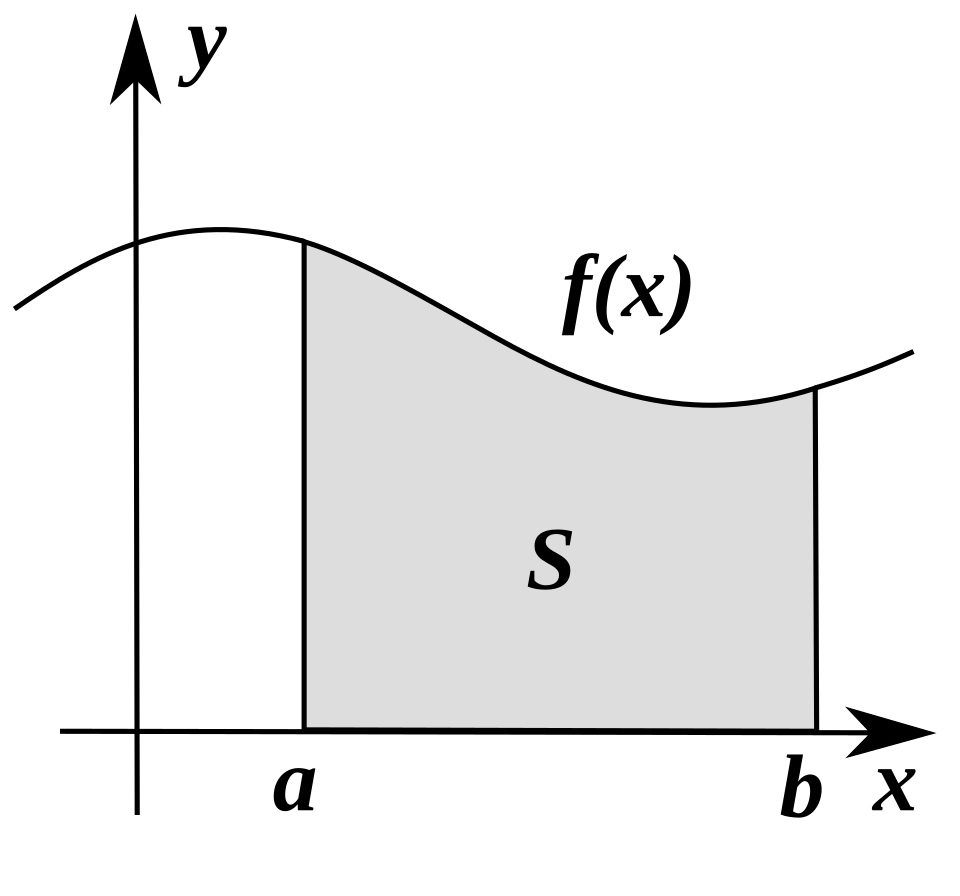
This diagram depicts a definite integral as the shaded area under a curve between $x=a$ and $x=b$ , labeled $S=\int_a^b f(x),dx$ . It emphasizes that integrals measure accumulated change by summing contributions over an interval, the same principle used in defining accumulation functions $F(x)=\int_a^x f(t),dt$ . The fixed upper limit $b$ in this figure reflects general integral notation and includes slightly broader context than the AP subtopic strictly requires. Source.

Sharper variations in f(t) cause faster increases or decreases in F(x).

These graphical insights allow students to interpret real-world accumulation without computing exact integral values.

Applied Meaning of Accumulation

Because many real-world problems involve measuring change over time or distance, accumulation functions provide a natural framework for interpreting integrals contextually. Students may encounter rates such as velocity, growth, decay, or flow. In each case, the accumulation function represents how much of the underlying quantity has built up since the starting point. This aligns directly with the syllabus requirement that accumulation functions express the accumulated change of a rate from the lower limit to the input.

Significance for AP Calculus AB

Mastering accumulation functions prepares students to connect integration, graphical analysis, and contextual interpretation. Recognizing that definite integrals model accumulated change equips students with a powerful conceptual lens for understanding everything from motion to population change, forming a foundation for the broader Applications of Integration topic.

FAQ

An accumulation function is defined with a fixed lower limit, creating a specific function whose value represents net accumulated change from that starting point. An antiderivative is a family of functions differing by constants.

Because the starting point is fixed, an accumulation function does not include an arbitrary constant and always satisfies F(a) = 0.

Yes. An accumulation function can decrease whenever the integrand becomes negative, even if it is positive on other parts of the interval.

The overall behaviour depends on the sign of the rate at each point, not the average sign over an interval.

If two accumulation functions share the same derivative, their underlying integrands are identical. However, they may differ by a constant because their lower limits may be different.

The choice of starting point fixes the vertical position of each accumulation curve.

The lower limit determines the baseline from which accumulation begins. Changing it shifts the reference point for measuring growth or decline.

This shift affects every value of the accumulation function, not just its behaviour near the starting point.

You interpret it by tracking the signed areas:

• Positive regions contribute increases.
• Negative regions contribute decreases.
• Rapid oscillations create alternating increases and decreases.

Even when the graph is complex, the accumulation function smooths these variations into a continuous measure of net change.

Practice Questions

Question 1 (1–3 marks)
Let a function F be defined by the accumulation function
F(x) = will display as integral from 2 to x of g(t) dt.
The graph of g(t) lies entirely above the t-axis on the interval 2 ≤ t ≤ 5.
State whether F(5) is positive, negative, or zero, and justify your answer.

Question 1 (1–3 marks)

• 1 mark for correctly identifying that F(5) is positive.
• 1 mark for recognising that g(t) is above the axis, so its integral accumulates positive area.
• 1 mark for clearly linking the sign of the area to the sign of F(5).

Maximum: 3 marks.

Question 2 (4–6 marks)
A function H is defined by the accumulation function
H(x) = will display as integral from 1 to x of v(t) dt,
where v(t) is a continuous rate function.
The graph of v(t) satisfies the following:
• v(t) is positive for 1 < t < 3
• v(t) is zero at t = 3
• v(t) is negative for 3 < t < 6
• The magnitude of v(t) for t > 3 is smaller than its magnitude for t < 3

(a) Determine whether H is increasing or decreasing on the intervals 1 < x < 3 and 3 < x < 6.
(b) Without computing any definite integrals, explain whether H(6) is positive, negative, or zero.
(c) Explain the significance of the starting point t = 1 in the definition of H.

Question 2 (4–6 marks)

(a)
• 1 mark for stating that H is increasing on 1 < x < 3 because v(t) is positive.
• 1 mark for stating that H is decreasing on 3 < x < 6 because v(t) is negative.
• 1 mark for explicitly linking the sign of v(t) with the monotonic behaviour of H.

(b)
• 1 mark for stating that H(6) is positive.
• 1 mark for explaining that the accumulated positive area from 1 to 3 is larger in magnitude than the accumulated negative area from 3 to 6.
• 1 mark for justification based on the given magnitudes of v(t).

(c)
• 1 mark for stating that the value H(x) measures accumulated change starting from t = 1.
• 1 mark for noting that H(1) = 0 because the limits coincide.
• 1 mark for identifying the starting point as defining the baseline from which all accumulation is measured.

Maximum: 6 marks.

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.