Understanding accumulation functions is essential for modeling how quantities build over time. Graphs and tables help students interpret how integrated rates produce meaningful accumulated values across intervals.

Interpreting Accumulation Functions Defined by Integrals

An accumulation function is a function defined by a definite integral whose upper limit is a variable. This structure captures how a quantity grows as the input increases and allows students to interpret accumulation from multiple representations, including graphs and tables.

Because accumulation functions express “how much has happened so far,” each output tells students how much total change has occurred relative to the starting point.

Understanding Integral-Based Accumulation on Graphs

Graphical representations of $f(t)$—the rate of change function—allow students to determine values of the accumulation function $F(x)$ by examining the area under the curve.

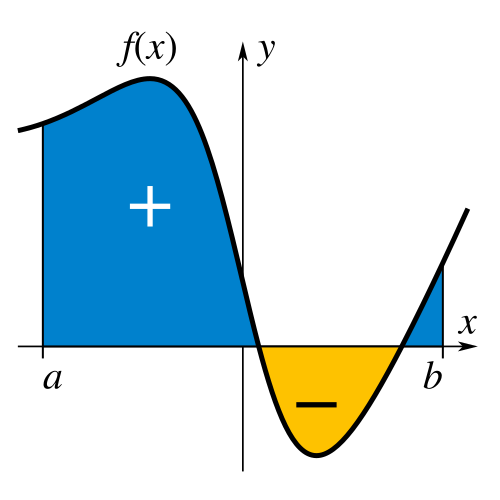
This diagram shows a continuous function with the definite integral $\int_a^b f(x),dx$ represented as the shaded region between $x=a$ and $x=b$. It reinforces that the accumulation function $F(x)=\int_a^x f(t),dt$ measures area as the upper limit varies. Although this image uses fixed bounds, the shaded-region idea is the same underlying concept for accumulation functions with a variable upper limit. Source.

Key Ideas When Interpreting Graphs

Students must connect the shape of the rate graph to how accumulation occurs. Important interpretations include:

• Positive regions above the horizontal axis increase accumulated value.

• Negative regions below the horizontal axis decrease the accumulated value.

• The slope of $F(x)$ matches the height of $f(x)$, because $F'(x)=f(x)$.

• Local maxima or minima of $F(x)$ occur where $f(x)=0$ and its sign changes.

These observations illustrate the essential idea that accumulation is directly tied to the signed area of the rate function.

When students read a graph of $f(t)$, they should view each section of the graph as contributing a positive or negative portion to the total accumulation.

Using Graphs to Infer Behavior of Accumulation

Graphical analysis helps students understand how $F(x)$ behaves even when it is not shown explicitly.

Interpreting Behavior from the Rate Graph

Students can determine trends in $F(x)$ by analyzing $f(t)$ on the graph. Important interpretations include:

• When f(t)>0, $F(x)$ is increasing.

• When f(t)<0, $F(x)$ is decreasing.

• When $f(t)$ has greater magnitude, $F(x)$ accumulates faster in the corresponding direction.

• When $f(t)$ crosses the axis, the accumulation function changes from increasing to decreasing or vice versa.

These interpretations help students understand how an accumulation function evolves over an interval without explicitly computing integrals.

Interpreting Tabular Representations of Accumulation

Tables often provide values of $f(t)$ at discrete inputs, requiring students to approximate accumulated change.

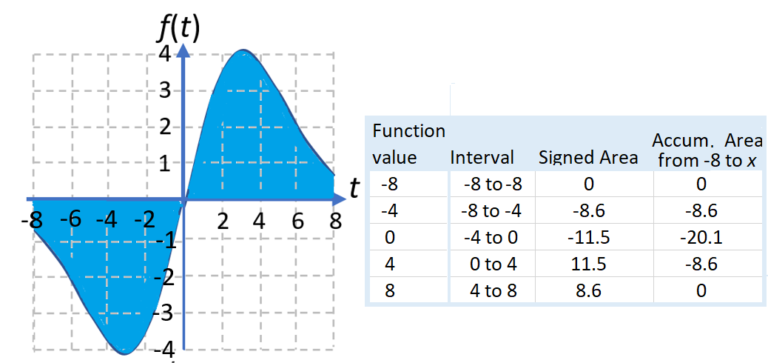
This figure pairs a graph of $f(t)$ with a table listing values of the accumulation function $F(x)=\int_a^x f(t),dt$. Each table entry displays the accumulated signed area from the starting point up to that $x$-value. The specific function and numbers exceed AP requirements, but the representation mirrors the graph–table relationships students must interpret. Source.

Principles for Working with Tables

When interpreting tables, students connect rate entries to approximate integrals. Key strategies include:

• Using left-, right-, or midpoint-based approximations to estimate accumulated area when exact integration is not possible.

• Observing sign changes in table entries to determine when accumulated value begins increasing or decreasing.

• Comparing magnitudes to assess how quickly the accumulation grows or shrinks across intervals.

• Noting the width of each subinterval, which directly influences the estimated contribution to accumulation.

These interpretations stress that a table communicates how a quantity builds, even when the underlying function is not shown graphically.

Understanding How Each Table Entry Contributes to Accumulation

Tables allow students to examine how each rate value affects the total accumulated amount over time. The accumulation function $F(x)$ increases when rate values are positive and decreases when they are negative, mirroring the graphical interpretation.

By connecting net change to integral-based accumulation, students interpret the table not as isolated data points but as components of a process of continuous accumulation.

Synthesizing Graphical and Tabular Interpretations

Whether presented as graphs or tables, accumulation functions convey the same underlying idea: each value of the accumulation function represents how much change has occurred from the starting point to the current input. Students must recognize that:

• The integral combines rate values over an interval into a single measure of accumulated change.

• Every graphical region or table entry contributes to that accumulation.

• The accumulation function is deeply tied to the behavior of the rate function through the fundamental relationship $F'(x)=f(x)$.

Essential Interpretation Skills

Students develop proficiency with accumulation functions by mastering the following interpretive tasks:

• Reading graphs of $f(t)$ and identifying how areas contribute to $F(x)$.

• Determining whether $F(x)$ is increasing or decreasing and analyzing its steepness.

• Approximating accumulation using table values of the rate function.

• Recognizing how sign, magnitude, and interval width affect accumulated totals.

• Relating observed patterns back to the AP emphasis: each value of an accumulation function represents the total accumulated change from the lower limit to the input.

These skills ensure students can interpret accumulation functions across multiple representations, fulfilling the requirements of the AP Calculus AB syllabus for this subsubtopic.