AP Syllabus focus:
‘Students translate verbal descriptions of changing quantities into definite integrals that represent net change or accumulated amount, then evaluate or estimate those integrals.’
This subsubtopic develops the essential skill of converting real-world or mathematical descriptions of varying quantities into definite integrals that represent accumulation or net change over a specified interval.
Understanding Accumulation and Net Change
When a quantity changes at a known rate of change, a definite integral accumulates all instantaneous changes over an interval to produce a single overall change. Students must learn to interpret verbal information, graphical information, or contextual descriptions and determine what integral correctly represents that accumulated amount. The focus is on setting up integrals—not on solving complex integrals—so clarity in translating descriptions to mathematical expressions is crucial.
Rate Functions as Inputs to Accumulation
A rate function describes how quickly a quantity changes with respect to an independent variable such as time. When the rate is known, accumulation arises naturally by interpreting the definite integral as the sum of infinitely many small contributions.
The figure shows a continuous function with the region under the curve shaded, illustrating how a definite integral represents accumulated change over an interval. The specific function is arbitrary and included only to demonstrate the concept of accumulation. Source.
Net change refers specifically to the overall increase or decrease in a quantity after all positive and negative contributions are combined.
Rate of Change: A function describing how one quantity varies with respect to another, often representing instantaneous growth, decay, or motion.
A single integral can represent net change whenever the rate can be expressed as a continuous function on the interval of interest.
Translating Verbal Descriptions into Integrals
Students must convert descriptive statements such as “the population increases at a rate of …,” “water flows into a tank at …,” or “the velocity of a particle is …” into definite integrals representing the amount accumulated over time. This involves identifying the correct rate function, determining the interval, and expressing the integral with appropriate limits. Understanding the meaning of the bounds is as important as identifying the integrand itself.
Identifying the Accumulated Quantity
To determine what is being accumulated, students should look for phrases that signal accumulation, such as total amount, net change, overall increase, or total quantity added. These phrases directly suggest the use of definite integrals. Once the accumulated quantity is identified, the rate of change becomes the integrand.
= Instantaneous rate of change of the quantity
= Start and end of the interval
A sentence that describes accumulation over time often contains contextual clues indicating whether the resulting integral represents a total amount added or a net balance after gains and losses.
Determining Integration Bounds
Understanding the interval is essential for correctly setting up an integral. The problem description will always provide either explicit bounds or contextual cues—such as starting and ending times—that must be interpreted. Students should ensure that limits reflect the direction of accumulation, usually from an initial time to a final time .
When the Rate is Positive, Negative, or Changing
The sign of the rate function affects the interpretation of the integral. A positive rate contributes to an increase, a negative rate represents a decrease, and a rate that switches sign requires additional conceptual attention. However, the definite integral automatically accounts for sign, producing net change without extra steps.
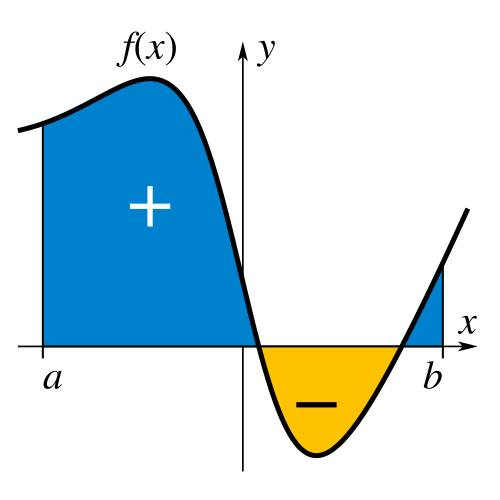
The graph highlights positive and negative signed areas, showing how a definite integral combines them to produce a single net value. The curve itself is arbitrary and serves only to illustrate the idea of signed accumulation. Source.
Only in problems about total accumulated magnitude—not net change—would a different expression be needed, but this subsubtopic focuses specifically on net change and accumulation as described by the AP specification.
Using Graphical and Tabular Information
Sometimes the rate function is not given algebraically but instead appears in a graph or table.
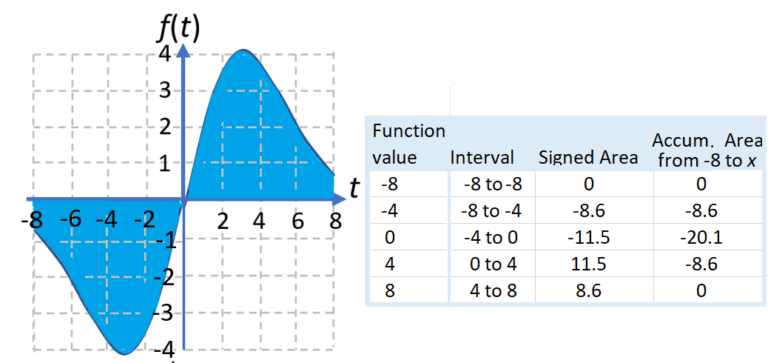
A graph–table pair illustrates how shaded regions represent signed contributions while a table tracks their cumulative total. The numerical values exceed syllabus needs but clearly demonstrate how accumulation is interpreted from graphical and tabular data. Source.
Students still identify the integral by examining the region under the rate curve or by interpreting table entries as instantaneous rates evaluated at discrete points. Even when numerical approximation methods are used later, the primary skill is writing the correct definite integral that captures the described accumulation.
Common Structures in Applied Contexts
Many real-world problems follow predictable patterns. When students learn to recognize these structures, setting up integrals becomes more intuitive.
Typical contexts include:
Growth or decay of populations, substances, or quantities governed by a rate function.
Fluid flow problems, where inflow or outflow rates determine the changing volume of a tank or reservoir.
Motion contexts, where velocity serves as the rate of change of position.
Economic or environmental rates, such as cost accumulation or pollutant discharge rates.
Each of these requires identifying a continuous rate function and establishing bounds that match the time or input interval described.
Step-by-Step Process for Setting Up Accumulation Integrals
Students can reliably convert a description into a definite integral by following a structured approach:
Identify the quantity whose total or net change is sought.
Determine the corresponding rate function, stated explicitly or implied contextually.
Extract the interval of accumulation from the description.
Write a definite integral of the form .
Confirm that the integrand and bounds match the stated scenario.
The Importance of Conceptual Interpretation
After setting up the integral, students should interpret what the integral represents in plain language. Understanding that the definite integral signifies the accumulated effect of a continuous rate over an interval aligns directly with the AP requirement for connecting integration to contextual meaning.
FAQ
Look for wording that indicates gains and losses should both be considered, such as net change, overall change, or final change in the quantity.
If the problem only refers to the amount added, total quantity accumulated, or total input, it is referring to accumulation rather than net change.
A key indicator is whether the rate can be negative. If so, the integral represents net change unless the question explicitly asks for total magnitude.
You can still represent net change with a single integral, but it may be written as a sum of integrals if the rate is defined piecewise.
For clarity, write one integral per section of the interval, ensuring the bounds align with where the rate expression changes.
If no numerical evaluation is required, you do not need to simplify the sum.
A definite integral for net change is valid as long as the rate has only removable or jump discontinuities and is integrable on the interval.
If the rate has essential or infinite discontinuities, the problem may require interpreting the integral as an improper integral.
In standard AP contexts, rates are chosen to be integrable, so handling discontinuities usually involves careful interpretation rather than new techniques.
Check whether the graph gives a complete rate-versus-variable relationship over the interval of interest.
You must know:
• the rate values (or shapes) across the interval
• the start and end points
• whether the graph implies positive or negative contributions
If any of these are missing, the graph may still support estimation but not a uniquely defined integral.
Bounds must match the interval over which the rate applies, not necessarily the interval where the underlying quantity is defined.
Errors typically arise when students:
• confuse the domain of the quantity with the domain of the rate
• overlook phrases like from t = 2 to t = 7
• assume the initial time is always zero
Accurate interpretation of the problem statement is essential for choosing correct limits.
Practice Questions
Question 1 (1–3 marks)
A tank receives water at a rate R(t) litres per minute, where t is measured in minutes. The rate is given by R(t) = 4 + 0.2t for 0 ≤ t ≤ 10.
(a) Write a definite integral that represents the total amount of water added to the tank over the first 10 minutes.
(b) State what this integral represents in context.
Question 1
(a) 1 mark
• Correct integral: ∫ from 0 to 10 of (4 + 0.2t) dt.
(b) 1 mark
• States that the integral represents the total amount of water added or accumulated over the interval.
Question 2 (4–6 marks)
A particle moves along a straight line with velocity v(t) metres per second, where t is measured in seconds. The velocity is shown in the table below.
t (s): 0, 2, 4, 6, 8
v(t) (m/s): 3, 5, 4, -1, -3
(a) Write a definite integral that represents the net change in the particle’s position from t = 0 to t = 8.
(b) Use a trapezium rule approximation based on the table to estimate the net change in position.
(c) Explain why the net change in position may be positive, negative, or zero, using the meaning of velocity as a rate of change.
Question 2
(a) 1 mark
• Correct integral: ∫ from 0 to 8 of v(t) dt.
(b) 2–3 marks
• 1 mark for using trapezium rule structure.
• 1–2 marks for correct substitution of values and obtaining a reasonable estimate of net change (follow-through marks allowed).
(c) 1–2 marks
• States that positive velocity contributes to forward movement and negative velocity to backward movement.
• Explains that the integral combines these signed contributions to give a net change which may be positive, negative, or zero depending on the balance of motion.

