AP Syllabus focus:
‘Definite integrals of rates, such as flow rates, growth rates, or velocity, are used to express accumulation and net change of physical or contextual quantities.’
Real-world quantities often change continuously, and definite integrals allow us to measure how much a quantity accumulates or changes over time when its rate of change is known.
Net Change in Applied Contexts
Understanding net change is essential in interpreting how a real-world quantity evolves when its rate of change is provided. In many applied problems, a function represents how quickly something is happening—such as how fast water flows, how rapidly a population grows, or how a particle’s velocity varies. The definite integral of this rate function over an interval provides the total accumulated effect, giving a direct measurement of the quantity’s overall change.
The Idea of Net Change as Accumulation
When a function describes a rate, accumulating its values over time reveals how much total change has occurred. This accumulation notion is central in interpreting applied integrals. The definite integral represents the sum of infinitely many small contributions of the rate, producing a meaningful, real-world quantity.
= Input variable, often representing time
= Quantity per unit time
This interpretation forms a powerful bridge between mathematical computation and real-world meaning. After identifying the rate function and interval, the integral describes how much the underlying quantity has increased or decreased.
Graphically, the net change in a quantity over an interval is represented by the signed area between the graph of its rate and the horizontal axis.
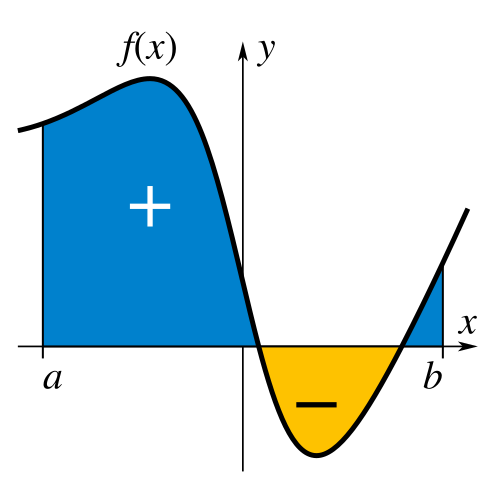
The graph shows a continuous rate function with regions above and below the axis whose shaded areas represent positive and negative contributions to net change. The visual emphasizes how opposite-signed areas combine to produce a single accumulated result. Any extra labels in the source image extend beyond AP Calculus AB requirements. Source.
Interpreting Net Change in Context
A definite integral does not merely provide a numerical value—it reveals how a system behaves. When solving applied problems, students should focus on the units of the rate and the real-world significance of the accumulated amount.
Key interpretive ideas include:
Total accumulation: The integral captures the total amount added to or removed from a system.
Units matter: Integrating a rate (e.g., liters per minute) over time yields a total quantity (e.g., liters).
Direction of change: A rate can be positive or negative, and the integral naturally accounts for gains and losses.
Interpreting net change requires connecting the value of the definite integral to the underlying scenario. Whether the context is physical, biological, economic, or environmental, the meaning arises from understanding what the rate signifies and how accumulation describes overall change.
Common Rate Functions in Real-World Scenarios
Subsubtopic 8.3.4 emphasizes interpreting definite integrals of various rates. In applied settings, three types of rate functions appear frequently:
Flow rates: Quantities entering or leaving a system, such as water pumped into a tank or pollutants entering a reservoir.
Growth rates: Biological or economic growth expressed as a time-dependent rate, including population growth and resource consumption.
Velocity functions: Rates of change of position in motion problems, where net change corresponds to displacement.
Each context requires careful attention to what is increasing or decreasing and how the rate influences final outcomes.
Steps for Interpreting Net Change from a Rate
To interpret an accumulation scenario effectively, students should follow a structured approach:
Identify the rate function and determine its meaning in the problem context.
Establish the interval over which the net change should be computed.
Integrate the rate, interpreting the integral symbol as representing accumulation over the chosen domain.
Translate the result into a contextual statement that clearly states what the integral represents and why it matters.
Verify units, ensuring that the interpretation aligns with the real-world quantity being measured.
A clear process ensures that the mathematical procedures support conceptual understanding, especially when interpreting answers rather than computing them.
Accumulation in Time-Dependent Systems
Many real-world systems evolve continuously, and the net change perspective provides insight into their behavior. When dealing with time-dependent systems, it is helpful to consider how the instantaneous rate contributes to the system’s state at each moment.
Examples of systems modeled with integrals of rates include:
Environmental systems: accumulation of rainfall over days, buildup of chemicals in a lake, or heat transfer into an object.
Mechanical systems: displacement, fuel consumption, or energy usage as functions of variable rates.
Economic systems: revenue generated from a fluctuating rate of sales or cost accumulation over time.
In each case, the definite integral provides a cumulative total that describes the system’s evolution from time to time .
For motion along a line, the definite integral of velocity over a time interval gives the particle’s displacement, so the area under a velocity–time graph represents net change in position.
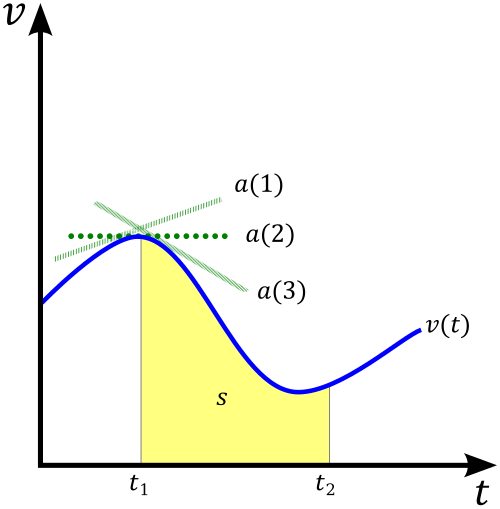
The diagram displays a velocity–time graph where the area under the curve signifies displacement and the slope represents acceleration. It illustrates net change as the accumulation of a rate over time. Some physics-based labels exceed syllabus requirements but do not detract from the conceptual alignment. Source.
Net Change Versus Total Change
In some contexts, the phrase net change specifically refers to the signed change in the underlying quantity. If the rate is negative at times, the definite integral reflects this sign, reducing the total and capturing overall direction. This is distinct from total magnitude changes such as total distance, which require absolute values and are treated elsewhere in the syllabus. For net change in applied contexts, interpreting the sign of the result is essential, as it indicates whether the underlying quantity has increased or decreased.
In motion contexts, the definite integral of a velocity function over a time interval accumulates the object’s displacement, and different time intervals may give different signed net changes.
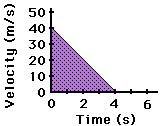
The figure presents several velocity–time graphs with shaded regions indicating displacement on specific intervals. Each shaded area corresponds to accumulated change, reinforcing the idea that measures net positional change. Some geometric annotations exceed AP Calculus AB scope but preserve conceptual clarity. Source.
The Role of Contextual Interpretation
AP Calculus AB emphasizes moving beyond symbolic manipulation to meaningful interpretation. Understanding what an integral represents requires synthesizing the rate, interval, units, and practical meaning. This subsubtopic develops the ability to articulate how accumulation models real phenomena, enabling students to translate mathematical results into clear statements about real-world processes.
The concept of net change forms a central theme in applied calculus, offering a framework for understanding how continuous change accumulates meaningfully over time.
FAQ
Check the sign of the rate. A positive value indicates an inflow or increase, while a negative value indicates an outflow or decrease.
If the function crosses zero, the system switches between gaining and losing the quantity. Interpreting the context carefully is essential, as some problems label inflow and outflow with separate functions rather than signs.
Net change describes the balance between gains and losses, regardless of whether the quantity itself can fall below zero.
A rate may be negative due to removal, decay, or reduction, and the integral measures the combined effect of increases and decreases without requiring the quantity to remain physically meaningful when extrapolated beyond zero.
Look for whether the context explicitly distinguishes between increases and decreases.
• If positive and negative contributions must remain distinct, interpret the integral as net accumulation.
• If the question stresses total magnitude gained, a different expression, often involving absolute values, is required.
Units of the integral reveal what the accumulated quantity represents. If a rate has units A per B, then integrating with respect to B results in units A.
This confirms whether the interpretation matches the scenario. If units do not match the expected physical quantity, the setup may need revision.
Net change sums all signed contributions. A negative region subtracts from the accumulated total, potentially offsetting large amounts of positive gain.
This makes careful graph reading important. A small interval with a significantly negative rate may drastically reduce or even reverse the overall net change.
Practice Questions
Question 1 (1–3 marks)
A tank is being filled with water at a variable rate R(t) in litres per minute, where t is measured in minutes. The rate is given by the table below for 0 ≤ t ≤ 4.
t (min): 0 1 2 3 4
R(t) (L/min): 6 8 9 7 5
Using a trapezium rule estimate, determine the approximate net amount of water added to the tank over the interval 0 ≤ t ≤ 4.
Question 1
• Correct use of trapezium rule structure with five data points (1 mark)
• Correct calculation of approximate integral:
(1/2)(6 + 2(8 + 9 + 7) + 5) = 35 litres (or equivalent working) (1 mark)
• Correct final statement of net water added (1 mark)
Total: 3 marks
Question 2 (4–6 marks)
A particle moves along a straight line with velocity v(t) in metres per second given by
v(t) = 4t − t²
for 0 ≤ t ≤ 4.
(a) Interpret the definite integral from 0 to 4 of v(t) dt in terms of the motion of the particle.
(b) Compute the net displacement of the particle on the interval 0 ≤ t ≤ 4.
(c) The particle changes direction when its velocity becomes negative. Explain how this affects the interpretation of the integral in part (b) in terms of net change.
Question 2
(a)
• States that the integral represents the net displacement of the particle over the interval (1 mark)
(b)
• Correct antiderivative, e.g. 2t² − t³/3 (1 mark)
• Correct evaluation at 0 and 4 giving net displacement 32 − 64/3 = 32/3 metres (1 mark)
(c)
• Recognises that negative velocity corresponds to motion in the opposite direction (1 mark)
• Explains that the integral sums signed displacement, so backward motion reduces the net change rather than adding to distance travelled (1 mark)
Total: 5 marks

