AP Syllabus focus:
‘The definite integral of a rate of change over an interval gives the net change of the underlying quantity on that interval, connecting antiderivatives and accumulation.’
The net change idea links definite integrals with accumulated change in a quantity, allowing rates to be turned into total increases or decreases over an interval.
Net Change and Accumulation
A central concept in AP Calculus AB is understanding that a definite integral represents accumulation of change. When a function describes a rate of change, integrating that rate over an interval gives the net change of the original quantity. This interpretation forms one of the most important bridges between differential and integral calculus, showing how instantaneous rates accumulate to produce overall change.
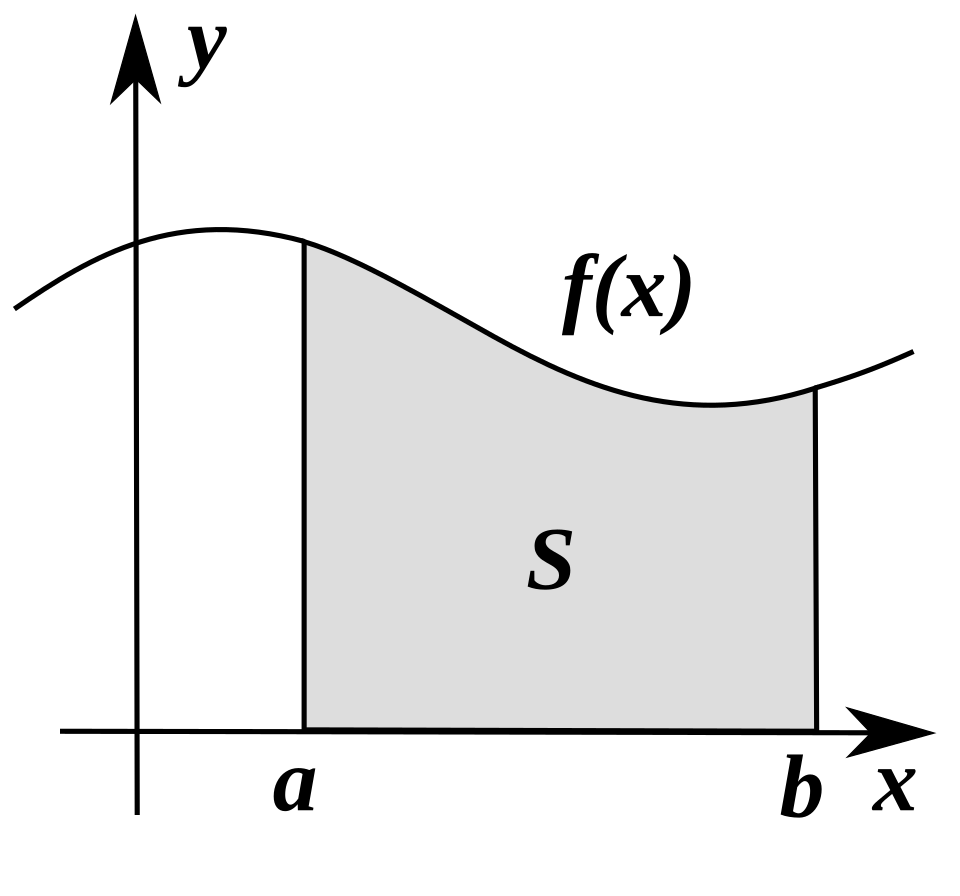
Visual representation of a definite integral as the accumulated area under a curve from to . The shaded region illustrates how integrating a rate over an interval produces a single net change value. This image includes only essential details—axes, curve, bounds, and shading—matching the level needed for AP Calculus AB. Source.
Understanding Rate Functions
A rate function is any function that gives the rate at which another quantity changes with respect to the input variable.
Rate of Change: A function describing how quickly another quantity increases or decreases with respect to an independent variable.
Typical rate functions include velocity as the rate of change of position, flow rate as the rate of change of volume, and growth rate as the rate of change of population.
Velocity–time graph with shaded regions illustrating how area represents displacement. This demonstrates net change: integrating velocity over a time interval gives overall change in position rather than total distance if velocity becomes negative. The diagram includes extra geometric annotations showing how displacement is computed from the area, slightly beyond the syllabus but aligned with AP-level expectations. Source.
Recognizing the structure of these problems allows students to identify when the rate is being integrated to recover accumulated change.
When a rate function is continuous on an interval, the definite integral over that interval represents the signed accumulation of the rate. Positive values increase the total, while negative values decrease it.
The Net Change Theorem
The Net Change Theorem formalizes the syllabus idea that definite integrals of rates yield total change. It expresses the relationship between a function and its derivative using definite integrals. Although AP Calculus AB does not require the theorem’s name, students must understand its meaning and apply it within problems.
= Derivative of the underlying quantity
= Bounds of accumulation
This equation captures the essential connection between derivatives and integrals: the derivative gives instantaneous change, and the integral of that derivative gives the total change.
Between two equation or definition blocks, include a normal sentence; here, the sentence reminds students that the integral produces signed, not absolute, change.
Net change reflects the overall increase or decrease of the underlying quantity. If the rate is positive on part of the interval and negative on another, the definite integral naturally accounts for both contributions. This aligns with the AP requirement that students interpret integrals as accumulation.
Interpreting Signed Accumulation
Signed accumulation means that the definite integral keeps track of direction. Positive rate values contribute positively, and negative rate values contribute negatively. The result may be less than the total distance, total volume, or total growth, depending on the context. Students must remember that net change differs from total amount added unless the rate is guaranteed to be nonnegative.
Key points include:
A positive definite integral indicates net increase.
A negative definite integral indicates net decrease.
A zero integral indicates that increases and decreases cancel out exactly.
Integrals over subintervals may be analyzed separately to understand the behavior of the underlying quantity.
This understanding is powerful because it allows students to describe long-term behavior using local, instantaneous changes.
Antiderivatives and the Fundamental Connection
The relationship between definite integrals and antiderivatives reinforces the conceptual interpretation of accumulation. If a rate function is recognized as a derivative, the change in the underlying function can be computed directly using antiderivatives. This makes the evaluation of net change efficient while still emphasizing accumulation.
= Underlying quantity
= Rate of change of that quantity
This expression emphasizes that definite integrals measure how much the original function changes between the endpoints of the interval. It also reinforces why rate accumulation yields a difference in function values.
Between any two formal blocks, a full sentence must appear, ensuring clarity and continuity while maintaining textbook-like rigor.
Recognizing Net Change in Applied Contexts
The AP specification highlights applied understanding. Students must identify situations in which a definite integral models the change in a physical, economic, biological, or other contextual quantity. To do this effectively, students should look for keywords indicating that a function represents a rate, such as “velocity,” “growth rate,” “influent flow,” “rate of heating,” “production rate,” or “rate of accumulation.”
When interpreting applied integrals, students should:
Identify the underlying quantity whose change is being described.
Recognize the given function as its rate of change.
Set appropriate bounds for the interval of interest.
Use the definite integral to express net increase or decrease.
Determine the real-world meaning of the numerical result.
Applied problems often rely on graphical information rather than explicit formulas. In those settings, students interpret accumulation by estimating the area between the rate graph and the axis, remembering that area below the axis represents negative contribution. This reinforces the syllabus emphasis that definite integrals represent net change through accumulation rather than solely through algebraic manipulation.
Setting Up Definite Integrals for Net Change
The ability to convert verbal descriptions into definite integrals is essential. Students must translate statements about changing quantities into integrals of rate functions. Clear translation depends on identifying the independent variable, the meaning of the rate, and the interval over which accumulation occurs.
When setting up net change integrals, students may follow this structured approach:
Identify the rate function provided.
Determine the underlying quantity associated with that rate.
Locate or infer the interval on which change is measured.
Write a definite integral of the rate over that interval.
Interpret the integral as the net change of the underlying quantity.
Through consistent practice with symbolic, graphical, and contextual forms, students develop a strong understanding of how definite integrals express accumulated change, fully aligned with the AP Calculus AB requirement for this subsubtopic.
FAQ
Net change comes from integrating a rate of change, not from directly substituting values into the original function.
While endpoint evaluation gives the actual change in the underlying function when its antiderivative is known, net change can still be computed from an integral even when the underlying function is not explicitly given.
This makes the concept especially useful when only rate data or graphs are available.
A definite integral can equal zero when positive and negative contributions cancel exactly.
This does not mean the rate was zero; it means that increases and decreases balanced out over the interval.
In real contexts, this often indicates a return to an initial state, such as a tank whose inflow and outflow average to no net gain.
Key elements include:
• whether the graph lies above or below the horizontal axis
• how long it remains there
• the relative size of positive and negative regions
A large negative area can outweigh smaller positive regions, determining the sign of the net change.
Even if the original quantity has corners or discontinuous derivatives, its rate function may still be integrable.
Net change uses accumulation of the rate, so smoothness of the underlying function is not required.
As long as the rate is integrable, net change is well defined.
Signed area preserves direction of change.
Positive area indicates increase, while negative area indicates decrease.
This is crucial for contexts like velocity, where reversing direction must reduce net displacement rather than add to it.
Practice Questions
A function g models a rate of change and is continuous on the interval 2 ≤ x ≤ 6. The graph of g lies below the x-axis on the entire interval. What does the definite integral from 2 to 6 of g(x) dx represent, and what can be concluded about its sign?
• 1 mark: States that the integral represents the net change of the underlying quantity on the interval 2 ≤ x ≤ 6.
• 1 mark: States that the value must be negative because the rate g(x) is entirely below the x-axis.
Total: 2 marks.
A particle moves along a straight line, and its velocity is given by the continuous function v(t). The velocity is positive for 0 ≤ t < 3, negative for 3 ≤ t ≤ 5, and positive again for 5 < t ≤ 7.
(a) Write an expression for the net change in the particle’s position on the interval 0 ≤ t ≤ 7 in terms of definite integrals.
(b) Explain in words why the value of the definite integral from 3 to 5 of v(t) dt must be negative.
(c) State whether the net change in position represents total distance travelled. Justify your response.
(a)
• 1 mark: Writes a correct expression for net change, for example, the integral from 0 to 7 of v(t) dt, or the sum of integrals over the three subintervals.
• 1 mark: Shows the integral structure clearly, such as explicitly writing the three definite integrals added together.
(b)
• 1 mark: States that the integral from 3 to 5 must be negative because v(t) is below the t-axis on this interval.
• 1 mark: Explains that negative velocity contributes negative signed area.
(c)
• 1 mark: States correctly that net change does not represent total distance travelled.
• 1 mark: Provides a justification, such as noting that negative velocity cancels positive contributions, whereas total distance requires integrating the speed.
Total: 6 marks.

