Comparing relative position allows statisticians to understand how individual data points stand within a distribution, supporting meaningful comparisons both within a dataset and across different datasets.

Understanding Relative Position in Context

Relative position describes how a particular value compares to the rest of the data. It focuses not on the raw value itself but on its standing within the distribution. This perspective is essential in statistical reasoning because data values gain meaning only when interpreted relative to the wider context of the dataset. The AP syllabus emphasizes that measures such as percentiles and z-scores help communicate a data point’s standing clearly and consistently.

Percentiles as a Measure of Position

Percentiles indicate the percentage of observations in a dataset that fall at or below a certain value. When first introducing the term percentile, it is important to recognize how widely used it is across fields such as education, health, and economics.

Percentiles allow for intuitive comparisons because they frame a data point relative to the entire data distribution rather than its absolute magnitude. For example, expressing a value as being at the 72nd percentile immediately conveys that it is higher than 72% of all observations. Between any two definition or equation blocks, a meaningful sentence is required, reinforcing how percentiles enable consistent interpretation across contexts.

Percentiles are particularly useful when comparing distributions measured on different scales. Because percentiles express relative standing using percentages, they remain unaffected by differences in units, measurement conventions, or data ranges.

Percentiles indicate the percentage of observations in a dataset that fall at or below a certain value.

This graph illustrates one definition of a percentile, mapping percent ranks to specific data values. The plotted points show how ordered observations correspond to percentile positions. The image includes a formal definition beyond AP scope, but the underlying concept aligns with the syllabus focus on percentiles as measures of relative position. Source.

Z-Scores as a Standardized Measure of Position

While percentiles provide a rank-based comparison, z-scores offer a numerical measure in terms of standard deviations from the mean. A z-score incorporates both the center and variability of a distribution, giving it a powerful role in statistical comparison.

Z-scores allow analysts to compare values from different datasets by placing them on the same standardized scale. This is especially important when distributions differ in center, spread, or measurement units. Because z-scores are standardized, they enable direct comparisons that would be impossible using raw data values alone.

EQUATION

Using z-scores helps determine whether a value is unusually high or low. A larger positive z-score means a value is far above the mean, while a large negative z-score indicates it lies far below the mean. These interpretations rely on the properties of the distribution’s center and spread rather than simple ranking.

Percentiles directly answer “what proportion is at or below this value?” while z-scores answer “how far, in standard deviations, is this value from the mean?”.

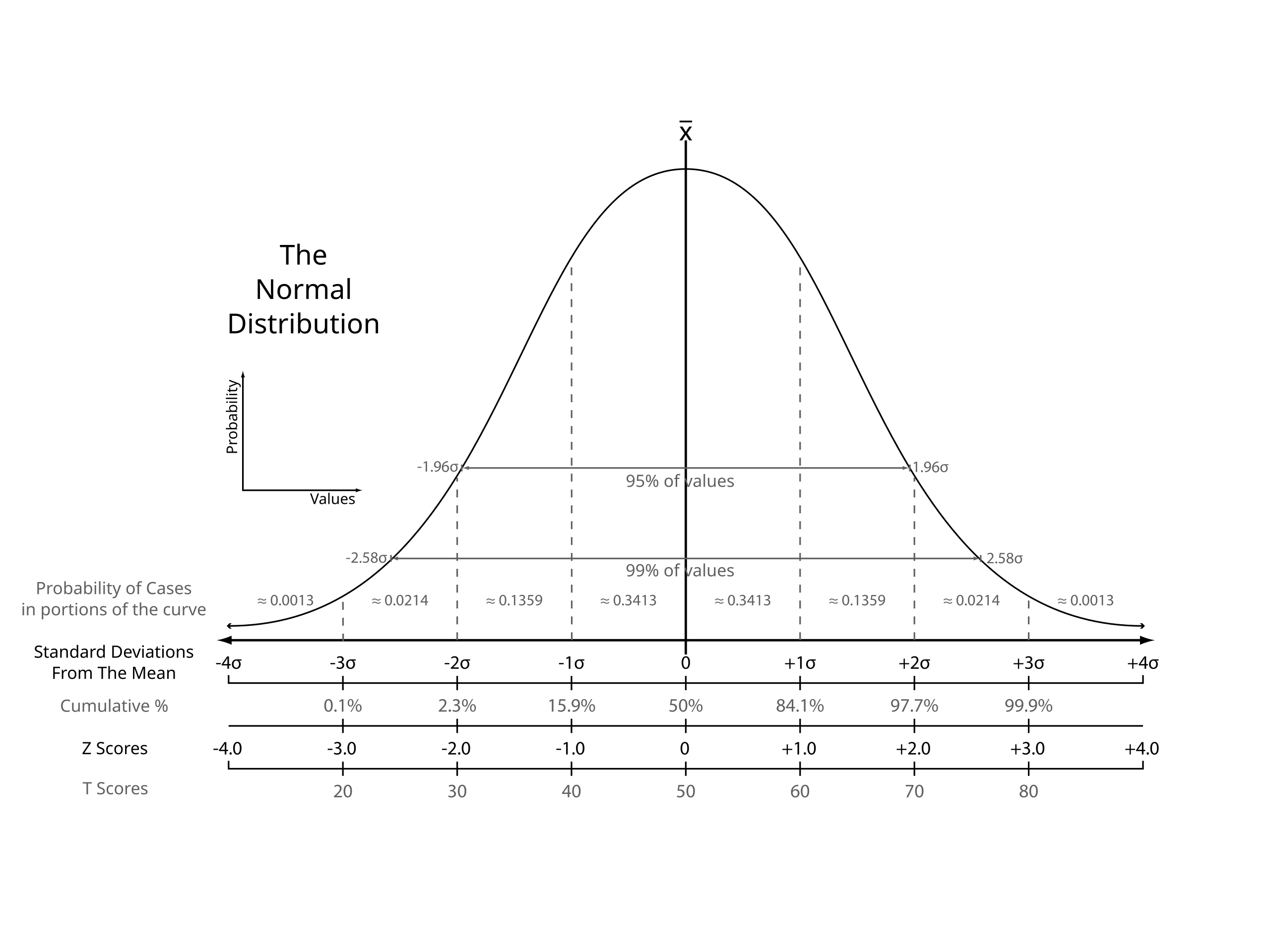
This standard normal distribution diagram shows z-scores aligned with cumulative percentages and percentile equivalents. It demonstrates how specific z-scores correspond to particular percentiles, such as 0 at the 50th percentile or ±1 near the 16th and 84th percentiles. The diagram includes T-scores, which exceed AP requirements but follow the same standardized framework. Source.

Comparing Percentiles and Z-Scores

Although both measures describe relative standing, percentiles and z-scores highlight different features of the distribution. Percentiles focus on ordering within the dataset, whereas z-scores incorporate the magnitude of deviation from the mean. This difference means the two measures are complementary rather than interchangeable.

Key Distinctions

• Percentiles

  • Communicate relative rank.

  • Do not consider how far values are from the center.

  • Useful for non-normal or skewed distributions.

• Z-scores

  • Communicate relative deviation using standard units.

  • Capture how unusual a value is.

  • Most interpretable when data are reasonably mound-shaped or symmetric.

Because the AP syllabus emphasizes effective comparison within and across datasets, students should be aware that percentiles may convey the general standing of a value, whereas z-scores provide a deeper quantification of the extremity of that standing.

Comparing Relative Positions Across Datasets

Comparisons across datasets often involve values measured in entirely different units or contexts. For instance, comparing heights measured in inches with test scores measured on a 100-point scale would make no sense using raw data alone. Standardizing with z-scores or expressing standing using percentiles eliminates these incompatible differences.

Important considerations when comparing values

• Use percentiles when the goal is to understand rank or relative order.

• Use z-scores when comparing across distributions with different centers or spreads.

• Larger absolute z-scores indicate more extreme positions.

• Higher percentiles indicate stronger relative standing within a dataset.

• Context is essential: neither measure is meaningful without understanding the distribution under consideration.

These principles align with Skill 2.D, which focuses on mastering comparisons of relative position and understanding the implications of these measures for data analysis. Both percentiles and z-scores ultimately help reveal how data points relate to the broader distributions they belong to, supporting informed and context-rich statistical reasoning.