Scatterplots reveal patterns in bivariate quantitative data, helping analysts determine whether variables appear related. Describing their characteristics supports clear communication and deeper statistical understanding.

Describing Scatter Plot Characteristics

Understanding the Purpose of Scatter Plot Description

A scatter plot displays paired observations for two quantitative variables and allows students to explore associations visually. The AP Statistics curriculum emphasizes that identifying the form, direction, strength, and unusual features of an association is essential for interpreting patterns in data. These characteristics help determine whether a relationship appears meaningful or may simply reflect random variation across observations.

Form of the Association

The form of a scatterplot refers to the general shape or pattern the data points appear to follow. Because scatterplots support the investigation of bivariate quantitative relationships, identifying form is a foundational observational step when interpreting data. The syllabus requires distinguishing between linear and nonlinear forms, as form guides the choice of analytical methods, including whether a linear model may be appropriate.

After identifying the form, students should consider whether deviations from this pattern are substantial enough to suggest alternative modeling approaches. Recognizing a nonlinear pattern, for example, may indicate the potential need for transformations or non-linear modeling techniques not covered in this subsubtopic.

Direction of the Association

The direction of the relationship describes whether the variables tend to increase or decrease together. Direction is highlighted in the AP syllabus as a core descriptive element of scatterplots and is necessary for developing later interpretations of correlation and regression.

Students should look for consistent upward or downward trends that reflect directional tendencies.

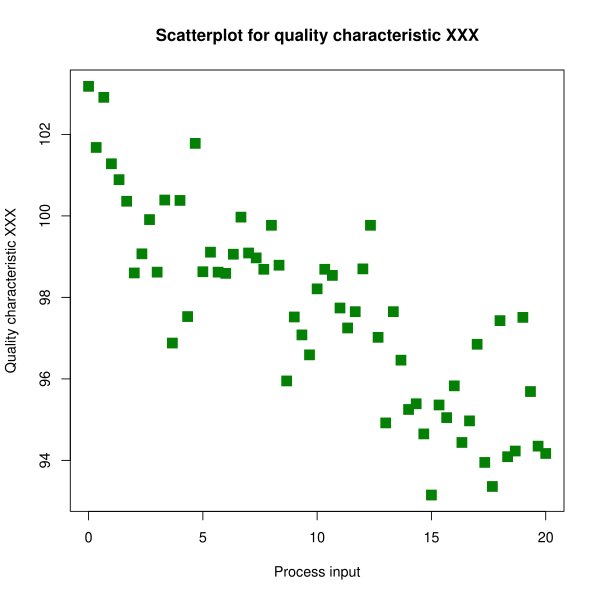
This scatterplot shows a downward, roughly linear association between two quantitative variables, illustrating a negative direction with moderate strength and natural variability. Source.

When direction is ambiguous or inconsistent across the range of data, this may signal a weak or nonexistent association.

Strength of the Association

The strength of the association describes how closely the data points follow the identified form. Strength is qualitative at this stage—terms like strong, moderate, or weak reflect how tightly points cluster around a general pattern. Strength is crucial because even a clearly positive or negative direction may have little predictive value if the relationship is weak.

When assessing strength, students should look for the density of points around the perceived form. Tighter clustering suggests stronger relationships, whereas widely scattered points indicate weaker associations. Strength helps determine whether a linear model could provide reasonable predictions, though formal assessment of model fit is addressed in later subsubtopics.

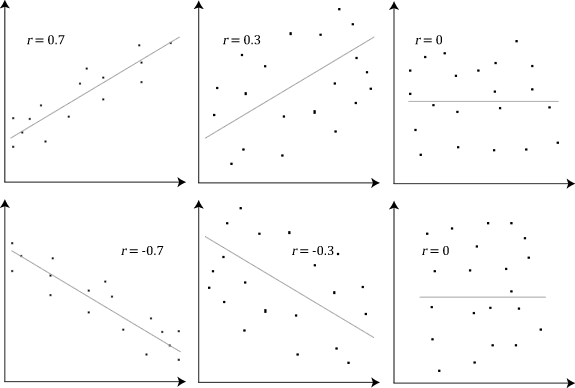
This grid illustrates differences in linear strength and direction, from strong positive to strong negative and near-zero associations, providing visual comparisons that reinforce descriptive terminology. Source.

Identifying Unusual Features

Unusual features provide critical context for interpreting scatterplots and can affect conclusions drawn about form, direction, and strength. The AP syllabus specifically lists clusters, gaps, and points with significant discrepancies as features that warrant attention. These irregularities can indicate subgroups, measurement issues, or influential values.

Common unusual features include:

• Clusters: Groups of points that suggest subpopulations or distinct behavioral patterns within the dataset.

• Gaps: Empty regions that interrupt otherwise continuous patterns and may signal missing values or discontinuities.

• Outlying points: Observations that lie far from the general trend, potentially affecting interpretation of any association.

• Points with large vertical discrepancies: Observations that differ substantially from what a trend might predict, later understood as large residuals.

Unusual features may influence conclusions about trend and strength, so they must be addressed explicitly whenever students describe a scatterplot. Their presence may also suggest limitations in using a linear model or may indicate potential influential or high-leverage points, which are explored further in later topics.

Methodology for Describing a Scatterplot

To meet AP expectations, students should describe a scatterplot in a structured manner that references each major characteristic in clear, concise language. A consistent descriptive process enhances communication and ensures that essential features of the relationship are addressed.

A recommended approach includes:

• Identify the form of the association (linear or nonlinear).

• State the direction (positive, negative, or none).

• Describe the strength (strong, moderate, weak).

• Note any unusual features, such as clusters, gaps, or outliers.

• Provide context-based interpretation only after all characteristics have been identified.

Normal sentences following these steps help maintain clarity when describing a scatterplot and reinforce the habits needed for formal statistical communication.

Interpreting Discrepancies Between Actual and Predicted Values

Although formal residual analysis appears later in the curriculum, the syllabus requires that students notice points with significant discrepancies between observed and predicted values. In scatterplot descriptions, these points appear vertically distant from the general pattern. Their presence suggests variability not captured by simple visual trends and highlights the importance of considering randomness and variation before making inferential claims.

Understanding these discrepancies builds foundational reasoning for later work with regression lines, residuals, and model evaluation, linking this subsubtopic to broader themes in two-variable analysis.