AP Syllabus focus:
‘Cover the addition rule for the probability that event A or event B or both will occur, explaining the formula P(A ∪ B) = P(A) + P(B) - P(A and B). This section aims to provide a detailed explanation of the rule, including how to account for the intersection of events to avoid double-counting probabilities. This rule is pivotal for calculating the union of two events and will be illustrated with examples for clearer understanding.’
Understanding how to determine the likelihood that at least one of two events occurs is essential in probability. The addition rule provides a systematic way to combine probabilities while avoiding overcounting outcomes shared by both events.
The Purpose of the Addition Rule
The addition rule is designed to quantify the probability of the union of two events. The union of events A and B refers to the event that either A occurs, B occurs, or both occur. Students often mistakenly add the probabilities of A and B without considering their overlap, which can lead to probabilities greater than 1. The addition rule corrects this by subtracting the probability of the intersection between the two events.
Understanding Event Unions
What the Union Represents
The union, written as A ∪ B, encompasses all outcomes belonging to A, B, or the overlap between them. Whenever two events share possible outcomes, those shared results must only be counted once when determining the probability of the union.
The union of two events A ∪ B is the event that includes all outcomes that are in A, in B, or in both.

A Venn diagram illustrating the union of events A and B, with the entire regions of both events shaded to show all outcomes in A, in B, or in both. Source.
The Role of the Intersection
The intersection, written as A ∩ B, contains outcomes that belong to both A and B. When students calculate probabilities of unions, any overlap must be carefully addressed to prevent double-counting, which is the main motivation behind the addition rule.
Defining the Core Concepts
When discussing the addition rule, several central terms arise that must be precisely understood before applying the rule.
Event Union (A ∪ B): The set of outcomes in which event A occurs, event B occurs, or both occur.
A sentence is required here before another block. The union is conceptually broad, as it captures the full range of possible outcomes across both events.
Event Intersection (A ∩ B): The set of outcomes shared by both event A and event B.
The intersection of A and B, written A ∩ B, collects outcomes that are in both events at the same time.
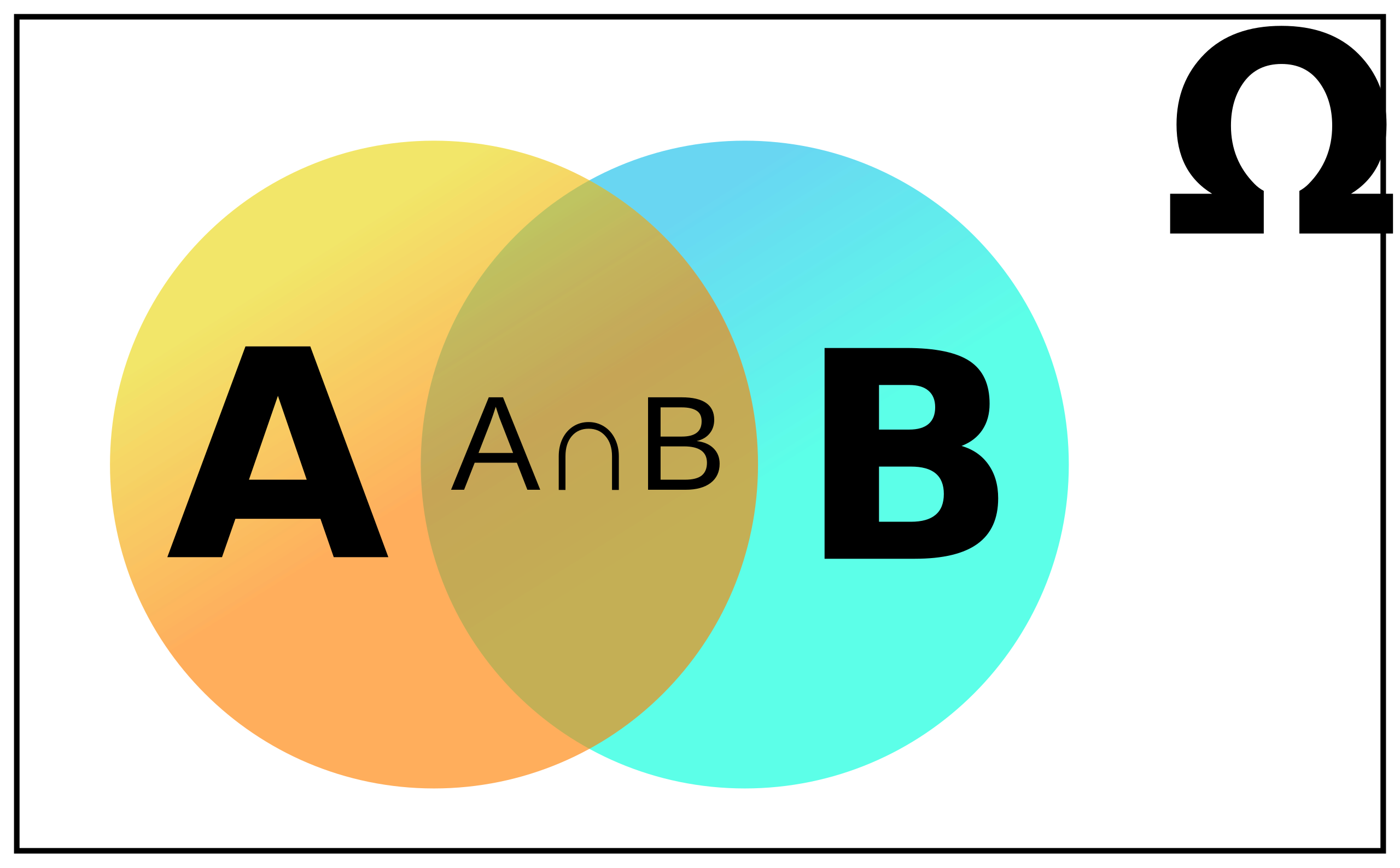
A Venn diagram depicting the intersection of events A and B, showing only the shared region where both events occur simultaneously. Source.
Understanding these structures is essential for recognizing why simple addition of probabilities does not always yield an accurate result.
The Addition Rule Explained
The addition rule formally states that the probability of event A or event B occurring equals the sum of the individual probabilities of the two events minus the probability that both events occur simultaneously. This ensures that shared outcomes are not counted twice.
EQUATION
= Probability that A or B or both occur
= Probability that event A occurs
= Probability that event B occurs
= Probability that events A and B occur together
This equation is essential because it applies broadly to any pair of events, regardless of whether they overlap.
Why the Subtraction Matters
When events have an intersection, those shared outcomes are counted once within P(A) and again within P(B). Without subtracting P(A ∩ B), the resulting probability artificially inflates the likelihood of the union. The subtraction restores accuracy and ensures the resulting value adheres to the probability scale, remaining between 0 and 1.
Situations Requiring the Addition Rule
The addition rule becomes particularly important when:
Events are not mutually exclusive
Mutually exclusive events have no intersection, making the subtraction unnecessary.
The problem explicitly asks for the probability that A or B occurs.
The events share possible outcomes or are related in a way that causes overlap.
A complete accounting of all possible outcomes is required to model a random process accurately.
Using the rule correctly ensures that all parts of each event are included—and only included once.
Distinguishing Special Cases
When Events Are Mutually Exclusive
If events A and B have no overlap, then P(A ∩ B) = 0. In this special scenario, the addition rule simplifies because no subtraction is needed.
When Events Overlap
Overlapping events require the full addition rule. The presence of a nonzero intersection means that the simple sum of individual probabilities would exceed the true probability of the union.
Conceptual Importance in Statistical Reasoning
The addition rule supports deeper statistical thinking by reinforcing that probabilities must reflect the structure of the underlying sample space. It underscores the importance of identifying relationships between events and illustrates how probability is fundamentally linked to counting methods and the organization of outcomes. Understanding the addition rule ensures that students avoid common errors in probability calculations while accurately modeling real-world situations involving multiple possible events.
By mastering this rule, students strengthen their ability to work with complex probability scenarios, combine probabilistic information correctly, and interpret the relationships between events within a sample space.
FAQ
Look for any outcomes that belong to both events in the context provided. If an outcome fits the description of both A and B, the events overlap.
You can also identify overlap by checking whether the situation allows for both conditions to happen together. If both can occur simultaneously in real life, the intersection is likely non-zero.
The addition rule is based on counting outcomes in the sample space, not on independence. Dependence affects how probabilities are calculated but does not change the structure of event unions.
Because the union simply collects all outcomes belonging to A, B, or both, the addition rule applies in any scenario where probabilities are defined.
Common errors include:
• Forgetting to subtract the intersection, leading to probabilities above 1.
• Substituting the wrong value for the intersection because it was not explicitly provided.
• Assuming events are mutually exclusive without checking whether overlap is possible.
Carefully identifying the intersection before using the rule helps avoid these mistakes.
A Venn diagram visually separates unique and shared regions of two events. This makes it easier to:
• See where outcomes overlap.
• Avoid counting shared outcomes twice.
• Understand the structure of the union, especially in word problems.
Visualisation is often the fastest way to confirm whether the addition rule requires subtraction of the intersection.
It helps estimate the likelihood that at least one of several desirable or undesirable outcomes occurs.
For example, businesses may assess the chance that a customer performs at least one profitable action, or environmental scientists may estimate the probability of experiencing at least one type of extreme event.
By quantifying combined risks or opportunities, the rule supports more informed planning and resource allocation.
Practice Questions
Question 1 (1–3 marks)
A school records whether students attend an after-school maths club (Event A) and whether they attend a science revision session (Event B).
The probability that a student attends the maths club is 0.32, and the probability that a student attends the science session is 0.41.
The probability that a student attends both sessions is 0.15.
Calculate the probability that a randomly selected student attends at least one of the two sessions.
Question 1 (1–3 marks)
• 1 mark: Correct application of the addition rule: P(A) + P(B) - P(A and B).
• 1 mark: Substitution of values: 0.32 + 0.41 - 0.15.
• 1 mark: Correct answer: 0.58.
Total: 3 marks.
Question 2 (4–6 marks)
At a theme park, visitors may watch a live show (Event A) or ride a popular rollercoaster (Event B). The park reports that:
• The probability a visitor watches a live show is 0.48.
• The probability a visitor rides the rollercoaster is 0.55.
• The probability a visitor does both activities is 0.29.
(a) Use the addition rule to calculate the probability that a visitor participates in at least one of these activities.
(b) Interpret your result in context.
(c) Explain why it would be incorrect to simply add the probabilities of A and B without adjustment.
Question 2 (4–6 marks)
(a)
• 1 mark: States or applies the addition rule.
• 1 mark: Correct substitution: 0.48 + 0.55 - 0.29.
• 1 mark: Correct answer: 0.74.
(b)
• 1 mark: Correct contextual interpretation, such as: Approximately 74% of visitors are expected to either watch a live show, ride the rollercoaster, or do both.
• 1 mark: Interpretation must reference the long-run relative frequency or expected proportion of visitors.
(c)
• 1 mark: States that adding the probabilities directly would double-count visitors who do both activities.
• 1 mark: Explains that subtracting the overlap ensures these visitors are only counted once when determining the probability of the union.
Total: 6 marks.

