This subsubtopic introduces how to identify and justify the two-sample z-interval for the difference between population proportions, emphasizing when and why this procedure is appropriate for inference.

Understanding When to Use a Two-Sample Z-Interval

A two-sample z-interval for the difference between population proportions is the appropriate confidence interval procedure when the goal is to estimate the true difference between two population proportions using data from two independent samples. This method relies on the approximate normality of the sampling distribution of the difference in sample proportions. It is used only when each sample produces a proportion based on categorically measured outcomes.

Why Compare Two Population Proportions?

When evaluating differences between groups—such as treatment vs. control, or demographic groups—researchers often measure categorical outcomes. The parameter of interest is the difference in population proportions, written as $p_1 - p_2$. Identifying the correct interval procedure ensures that the resulting estimate properly reflects sampling variability and supports valid statistical interpretation.

Key Components of the Two-Sample Z-Interval

The two-sample z-interval uses paired sample information to produce an interval estimate of the likely range of $p_1 - p_2$. The sampling distribution for the difference in sample proportions, $\hat{p}_1 - \hat{p}_2$, becomes approximately normal under appropriate conditions related to independence and sample size.

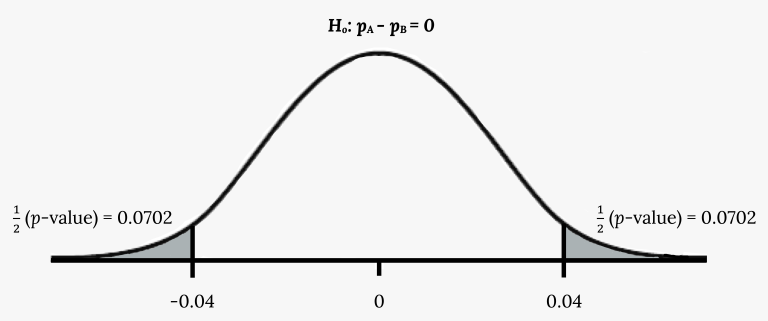
This figure displays the normal distribution for the difference in sample proportions under the null hypothesis, illustrating how the sampling distribution of $\hat{p}_1 - \hat{p}_2$ is modeled. Although shading relates to p-value regions, which exceeds this subsubtopic’s scope, the core visual emphasizes the approximate normality needed for applying a two-sample z-interval. Source.

The Point Estimate

The primary statistic calculated from the sample data is the difference in sample proportions, $\hat{p}_1 - \hat{p}_2$. This value represents the observed difference and serves as the center of the confidence interval.

Selecting an appropriate point estimate is essential because the confidence interval builds around it to reflect potential sampling error.

Requirements for Using the Procedure

Before applying the two-sample z-interval, students must verify that the study design and data behavior justify its use. Independence and sample size adequacy are central requirements.

Independence Between and Within Samples

The samples must come from independent groups. No individual may belong to both samples, and the data-generating process must avoid any structural linkage between the groups. Random sampling or random assignment helps ensure independence.

Sufficient Sample Size for Normality

Approximate normality of the sampling distribution is necessary to use the z-based interval. This requires that both samples have sufficiently large counts of successes and failures.

This condition ensures that the z-interval yields accurate and reliable inference.

Structure of the Confidence Interval

The two-sample z-interval has a general structure that follows the form:
point estimate ± margin of error.
The margin of error reflects uncertainty arising from sampling variability.

EQUATION

This structure reinforces that the interval captures plausible values of the true difference between population proportions based on observed data.

A confidence interval based on this formula will widen or narrow depending on sample sizes, variability within each sample, and the selected confidence level.

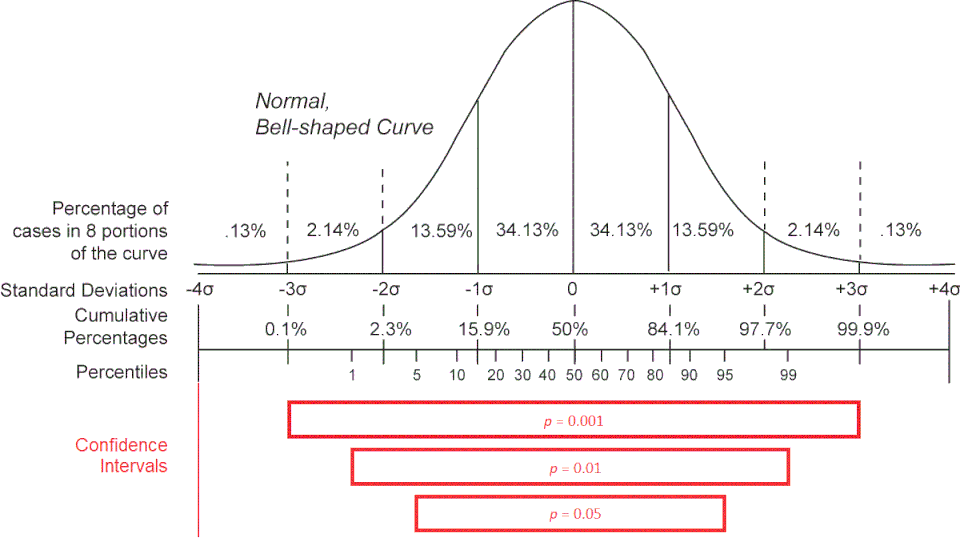
This diagram displays several confidence intervals of different confidence levels drawn on a normal curve. Higher confidence levels require wider intervals, visually connecting confidence level to interval width. Although the figure represents a generic normal distribution, the same conceptual structure underlies z-based confidence intervals for proportions and for the difference between two proportions. Source.

When the Two-Sample Z-Interval Is the Correct Choice

Choosing the correct interval procedure requires assessing the statistical goal, the nature of the data, and the study design. The two-sample z-interval is appropriate under the following circumstances:

• The research question focuses on estimating the difference between two population proportions, $p_1 - p_2$.

• The data for each group consist of categorical outcomes classified into two categories (success/failure).

• The two samples are independent, generated through random sampling or random assignment.

• Success–failure conditions for each sample indicate that normal approximation is reasonable.

• The study does not involve matched pairs or dependent samples, which require different methods.

Interpreting the Purpose of the Interval

The goal of this procedure is not to test a hypothesis but to estimate a range of plausible values for the difference in population proportions. This range communicates uncertainty and supports claims about whether meaningful differences between groups may exist. The interval reflects natural sample-to-sample variability and helps quantify the degree of confidence in the estimation process.