A confidence interval becomes meaningful only when its numerical bounds are translated into clear, contextual statements. Interval estimates express statistical results using real-world units and interpretation.

Understanding Interval Estimates

An interval estimate is a contextualized statement that communicates what the calculated confidence interval suggests about the population parameter. It transforms the abstract numerical interval into language that directly relates to the study setting. Interval estimates do not add new calculations; instead, they articulate the meaning of the interval bounds using the original measurement scale.

Because confidence intervals represent ranges of plausible values for a population proportion, an interval estimate must reflect this uncertainty while grounding the interpretation in the study’s population and variable.

Connecting Numerical Bounds to Context

After constructing the confidence interval for the difference of two population proportions, $(\hat{p}_1 - \hat{p}_2) \pm z^* \sqrt{(\hat{p}_1(1-\hat{p}_1)/n_1) + (\hat{p}_2(1-\hat{p}_2)/n_2)}$, students must express what the interval implies in practical terms. The emphasis is on translating statistical notation into clear, interpretable language.

EQUATION

The interval estimate explicitly communicates the meaning of the upper and lower bounds using the variable being measured. This translation is essential because statistical conclusions must be understandable to audiences without mathematical expertise.

Written numerically, the confidence interval becomes the interval estimate: a lower bound and an upper bound that bracket plausible values for the true difference in population proportions.

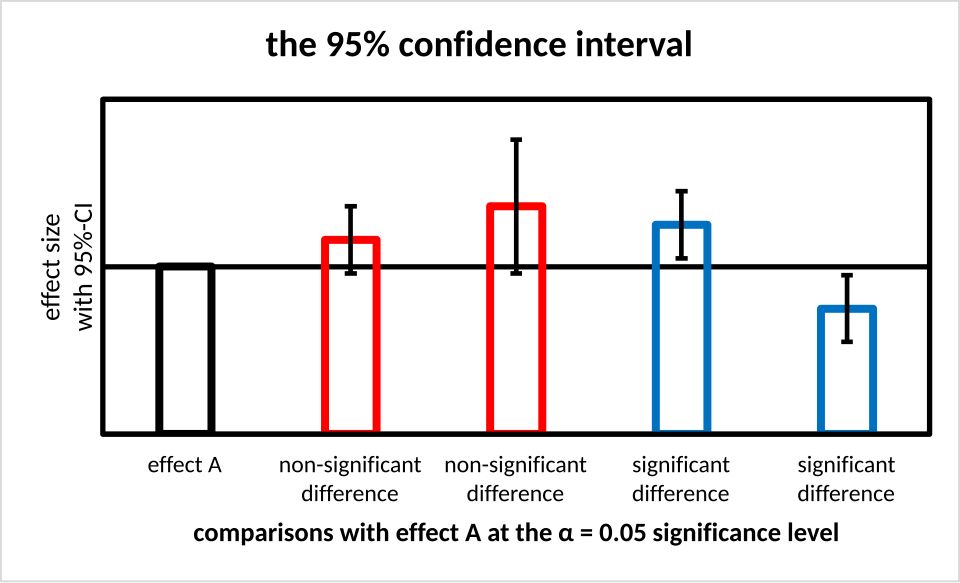
Bar chart illustrating several sample estimates with their associated 95% confidence intervals drawn as vertical error bars. Each error bar shows the lower and upper endpoints of the interval estimate around a point estimate. Although shown for means, the visual structure of an interval estimate is identical to that used for proportions. Source.

Key Elements of Effective Interval Estimates

An effective interval estimate incorporates several essential features that ensure clarity and alignment with AP expectations.

1. Reference to the Population

An interval estimate must specify the populations represented by the two sample proportions. It is incorrect to state interpretations solely in terms of the samples because confidence intervals always generalize from sample data to broader populations.

2. Description of the Variable

The interval must be tied to the category or event being measured. Because we are dealing with population proportions, the statement should identify the categorical outcome of interest and its meaning within context.

3. Presentation in Original Units

Proportions are naturally unitless, but their interpretation often relates to meaningful descriptors of group differences. When appropriate, interval estimates may be expressed as absolute differences in proportions, percentage-point differences, or directional comparisons.

4. Connection to Confidence Level

Although interval estimates focus on translating bounds, they remain grounded in the logic of C% confidence. This phrase conveys that the method—rather than a specific interval—captures the parameter in roughly C% of repeated samples.

Even though we report only one interval estimate in a study, the confidence level describes what would happen if we repeatedly took similar samples and built new confidence intervals each time.

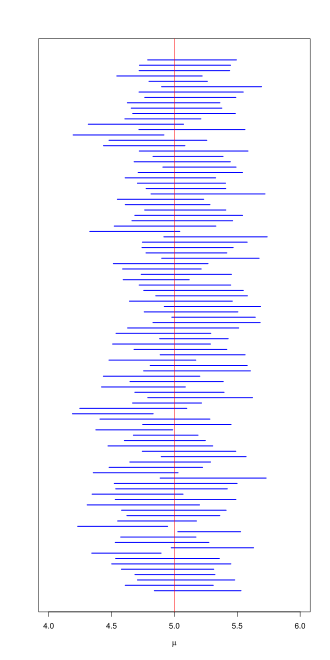
Plot of 100 separate 95% confidence intervals drawn from repeated random samples, with a vertical red line marking the true parameter value. Most intervals cross the true value, visually demonstrating the long-run coverage interpretation of a confidence level. Although based on means, the concept mirrors how confidence intervals function for differences in proportions. Source.

5. Expression of Uncertainty

Interval estimates must avoid definitive claims. Instead, they emphasize plausible values, using language such as:

• “likely lies between”

• “is estimated to fall within”

• “is consistent with values from ___ to ___”

Process for Constructing Interval Estimates

Students can rely on a structured approach to produce coherent interpretations.

Step 1: Identify the Parameter

State that the confidence interval estimates the difference in population proportions. Clarify which population corresponds to $p_1$ and which corresponds to $p_2$.

Step 2: Relate Bounds to Real-World Meaning

Translate each endpoint of the interval into the context of the categorical variable. This ensures that the interpretation never drifts into generic numerical description.

Step 3: Use Clear, Non-Technical Language

Even though the calculations rely on formulas, the final interval estimate must be readable and accessible. This is especially important when interval estimates appear in research settings or applied contexts.

Step 4: Preserve Directionality

The order $(p_1 - p_2)$ must remain explicit in the interpretation. Reversing direction can lead to incorrect claims about which population has a higher or lower proportion.

Step 5: Maintain Statistical Integrity

Avoid conclusions that imply certainty. Interval estimates should always acknowledge the inherent randomness of sample-based inference.

Practical Characteristics of Interval Estimates

Well-crafted interval estimates exhibit several recognizable strengths:

• They anchor interpretation in the confidence interval while reframing it into applied meaning.

• They avoid excessive precision by refraining from over-interpreting boundary values.

• They communicate implications for population differences without implying causation.

• They focus on what the interval suggests about plausible differences, not on what it proves.

Importance of Contextual Translation

AP Statistics emphasizes that meaningful interpretation is as critical as correct computation. The specification requires that students “present the confidence interval in the context of the original data.” This translation step ensures that statistical results function as tools for reasoning about real-world situations, not merely mathematical outputs. Interval estimates bridge the gap between numerical inference and applied understanding, reinforcing the purpose of confidence intervals in statistical analysis.