This subsubtopic explains how to choose the appropriate procedure for constructing confidence intervals for population means when the population standard deviation is unknown.

Understanding When to Use a t-Interval

When estimating a population mean, the one-sample t-interval is used whenever the population standard deviation is unknown and the sample standard deviation provides the best available estimate. This choice reflects the reality that most real-world data sets do not come with a known population standard deviation, requiring an approach that incorporates additional uncertainty. Because the t-distribution accounts for this uncertainty, it becomes the foundation for valid inference about a population mean.

Because σ is unknown, the standardized statistic follows a Student’s t-distribution rather than a standard normal distribution.

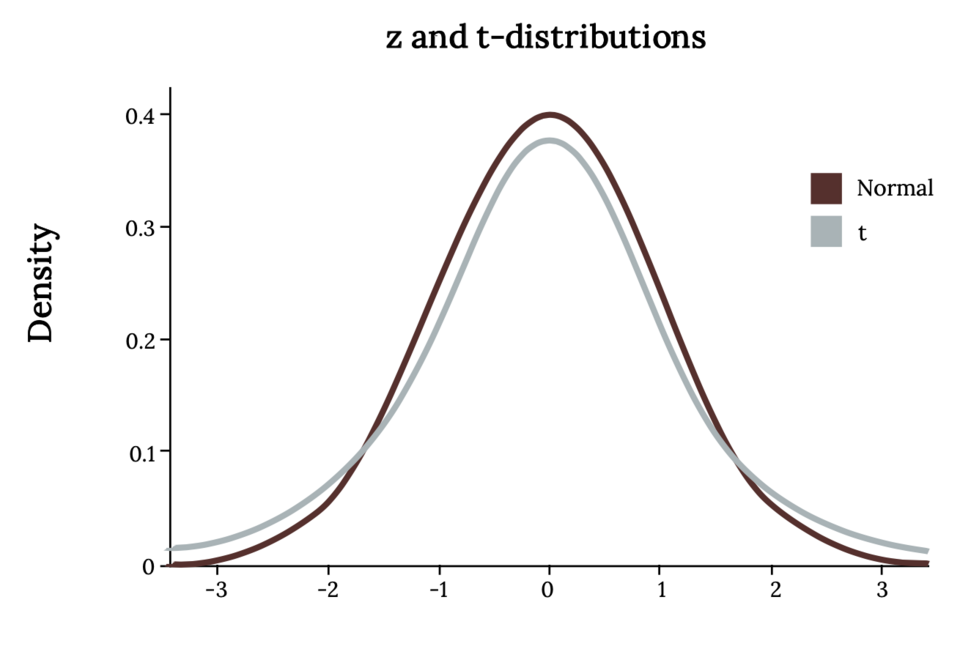
This figure compares the normal distribution with several t-distributions, showing heavier tails for smaller degrees of freedom and convergence toward normality as degrees of freedom increase. Source.

Key Features of the One-Sample t-Interval

A one-sample t-interval relies on information from a single random sample and is appropriate under conditions ensuring independence and approximate normality of the sampling distribution. The reasoning behind this interval centers on estimating the population mean while acknowledging potential error introduced by relying on sample statistics.

Before introducing formal notation, it is useful to recognize that t-based inference is designed to adjust for the extra variability that arises when replacing the population standard deviation with the sample standard deviation.

EQUATION

The formula highlights how both sample variability and desired confidence level influence the interval's width.

Selecting the Procedure When σ Is Unknown

Because the population standard deviation σ is almost never known, the appropriate procedure is the one-sample t-interval rather than a z-interval. This distinction is essential for AP Statistics students, as using the wrong procedure results in incorrect conclusions. The t-distribution’s heavier tails offer a more conservative and realistic model when estimating variability from sample data.

Why Sample Standard Deviation Matters

The sample standard deviation introduces uncertainty because it is only an estimate. The t-distribution compensates for this by widening the interval relative to a normal-based interval. As sample size increases, the t-distribution approaches the normal distribution, meaning the procedure becomes more precise with larger samples.

Matched Pairs and the One-Sample t-Interval

Some studies involve matched pairs, a design in which each observational unit provides two related measurements. These pairs often represent “before–after” scenarios or matched individuals with similar characteristics. In such cases, inference must consider the difference between paired observations rather than the raw values themselves.

Once differences are calculated, they form a single list of quantitative values that behave like a one-sample dataset. This transformation allows the matched pairs situation to be handled using the same t-interval procedure applied to a single quantitative variable.

The key is that the analysis depends on the mean and standard deviation of these differences, not of the original measurements. Treating differences as a single sample ensures that the interval accurately reflects the direction and magnitude of change across pairs.

For a matched pairs setting, compute the difference for each pair and treat these differences as a single sample of quantitative data when constructing the t-interval.

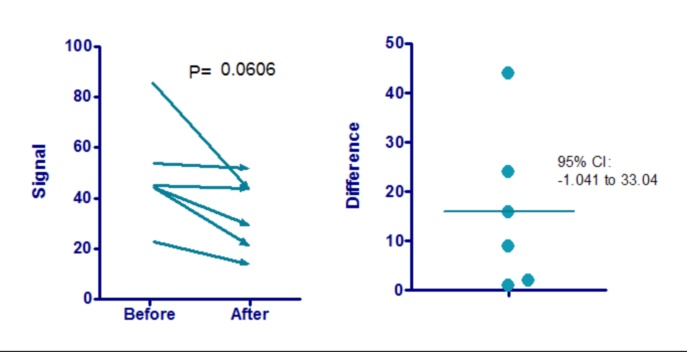
The left panel shows paired observations linked for each subject, while the right panel displays the distribution of differences and their confidence interval, illustrating how paired data become a single sample of differences for t-interval construction. Source.

Procedure for Applying the Correct Interval

Students should be able to identify when to use the one-sample t-interval and how the structure of a study directs this choice. The following points summarize the procedural reasoning:

One-Sample t-Interval for a Mean

Use this when:

• σ is unknown, and the sample standard deviation must be used instead.

• The data come from a single random sample of quantitative values.

• Conditions such as independence and approximate normality are satisfied.

Matched Pairs t-Interval

Use this when:

• The study collects paired observations on a single group of individuals or units.

• The analysis focuses on the differences between paired values.

• These differences can be treated as a single set of quantitative data.

Important Considerations

• The form of the interval does not change between one-sample and matched pairs procedures; only the data used in the calculation differ.

• Sample size and the shape of the distribution influence how reliably the procedure performs.

• Independence in data collection is essential for valid inference.

Distinguishing This Procedure from Others

Students must differentiate the one-sample t-interval from:

• z-intervals, which require known σ and thus apply in only limited scenarios.

• Two-sample intervals, which are used when comparing means from two independent groups rather than estimating a single mean or paired difference.

• Non-inference procedures, which might summarize sample data but do not quantify uncertainty about the population.

The focus of this subsubtopic is knowing which confidence interval procedure is appropriate and why the one-sample t-interval—along with its matched pairs adaptation—is the correct and justified choice in most situations involving unknown population variability.