AP Syllabus focus:
‘The margin of error for a t-interval is found using the critical value t* (based on degrees of freedom n-1 and desired confidence level) and the standard error of the sample mean, calculated as s/√n where s is the sample standard deviation. The margin of error increases with a larger critical value t* or larger standard error (s/√n), indicating less precision in the estimate.’
AP Statistics relies on understanding how uncertainty affects estimates; the margin of error in a t-interval quantifies this uncertainty when the population standard deviation is unknown.
Understanding the Margin of Error in t-Intervals
The margin of error (ME) represents how far the sample mean might reasonably be expected to vary from the true population mean due to sampling variability. In a t-interval, the margin of error incorporates both the estimated variability in the sample and the required level of confidence.
When constructing a confidence interval for a population mean using the t-distribution, the margin of error reflects two essential components: a critical value from the t-distribution and the standard error of the sample mean. These quantities work together to determine how wide the confidence interval will be.
This diagram illustrates a point estimate with a symmetric confidence interval, showing the margin of error as the distance from the center to either endpoint. It emphasizes how the interval width is determined by twice the margin of error. Any numerical labels included offer a specific example but are not required by the syllabus. Source.
Margin of Error (ME) equals t* multiplied by s divided by the square root of n.
t* is the critical value from the t-distribution based on confidence level and degrees of freedom.
s is the sample standard deviation.
n is the sample size.
Because the population standard deviation is unknown, students rely on the sample standard deviation to form an estimate of variability. This introduces additional uncertainty, which is why the t-distribution—not the normal distribution—is used.
Components That Determine the Margin of Error
The Critical Value t*
The critical value t* arises from the t-distribution and depends on both the chosen confidence level and the number of degrees of freedom (df = n − 1). As degrees of freedom increase, the t-distribution becomes narrower and approaches the standard normal distribution, reducing the magnitude of t*.
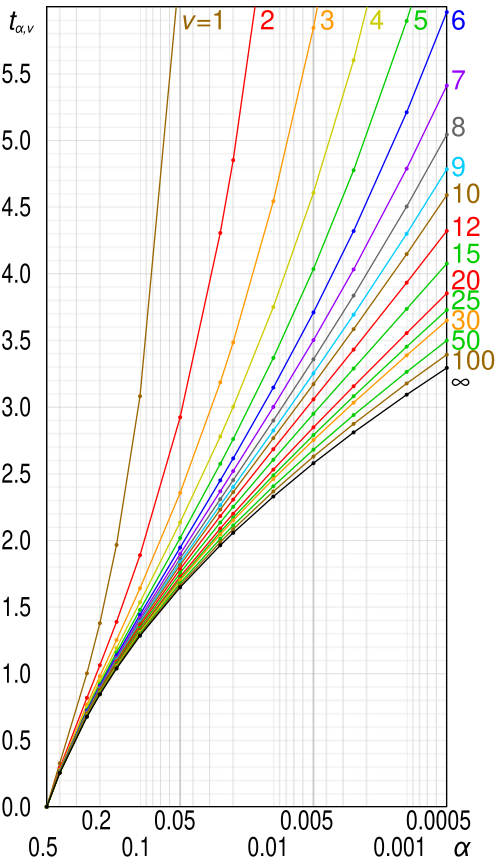
This graph shows how the critical value t changes with alpha for different degrees of freedom. It demonstrates that smaller degrees of freedom require larger critical values, increasing the margin of error. The multiple curves offer detail beyond the syllabus but reinforce the relationship between confidence level, degrees of freedom, and t.* Source.
Critical Value t*: A multiplier from the t-distribution that determines how far estimates must extend from the sample mean to achieve a specified confidence level.
A higher confidence level always requires a larger critical value because more certainty demands a wider interval. Even with the same data, increasing confidence inevitably expands the margin of error.
The Standard Error of the Sample Mean
The standard error (SE) measures how much variation we expect in sample means when repeatedly sampling from the population.
Standard Error equals s divided by the square root of n.
s is the sample standard deviation.
n is the sample size.
The standard error decreases as sample size increases, reflecting the stabilizing effect of more data. A smaller standard error directly reduces the margin of error, narrowing the confidence interval and improving precision.
Between these two components, the standard error typically has a more dramatic impact on the width of the margin of error because it changes with sample size, whereas changes in the critical value are more gradual.
How the Margin of Error Influences Precision
The syllabus emphasizes that the margin of error increases when either the critical value or the standard error becomes larger. This relationship highlights how the structure of a study affects the precision of its estimates.
Effects of a Larger Critical Value
A larger t* value means the interval extends farther from the mean. Situations that create larger critical values include:
Using small sample sizes, which lower degrees of freedom
Selecting very high confidence levels (such as 99% instead of 95%)
This increased margin of error makes conclusions less precise, reflecting the additional uncertainty inherent in smaller samples or more demanding confidence requirements.
Effects of a Larger Standard Error
A larger standard error indicates more variability in the sample estimate. Several factors contribute to increased SE:
A large sample standard deviation
A small sample size
Because s reflects the spread of the sample data, a dataset with substantial variability naturally leads to a broader interval. Likewise, a small n means less information is available to estimate the mean, magnifying uncertainty.
Interpreting the Margin of Error in Context
Understanding the margin of error is critical for interpreting confidence intervals meaningfully. A wide margin of error tells us that the data provide a less precise estimate of the population mean. Conversely, a small margin of error suggests a more accurate estimate.
Students should remember that precision is influenced by design choices. Increasing the sample size, for instance, is one of the most effective ways to reduce the margin of error without changing the confidence level. Similarly, recognizing the role of sample variability encourages careful attention to data collection methods that limit unnecessary variation.
Ultimately, the margin of error embodies the balance between confidence and precision. The t-interval framework accounts for the uncertainty introduced by estimating population variability with sample statistics, and understanding its components allows students to interpret statistical results responsibly and thoughtfully.
FAQ
The t-interval must account for additional uncertainty because the population standard deviation is unknown and replaced with the sample standard deviation. This makes the estimate less stable, especially with small samples.
As a result, the critical value from the t-distribution is larger than the z critical value for the same confidence level, producing a wider margin of error.
Moderate skewness does not invalidate the t-interval if the sample size is reasonably large, but noticeable skewness in small samples makes the margin of error less trustworthy.
This is because the standard error may not accurately represent the variability of the sample mean when the data deviate strongly from normality.
The standard error decreases with the square root of n, meaning each additional observation has a diminishing effect.
This creates a point at which adding more sample units results in only small improvements in precision, making dramatic reductions in margin of error increasingly difficult.
Yes. Differences in sample standard deviation lead directly to differences in standard error, which affects the margin of error.
A highly variable dataset produces a larger margin of error than a more consistent dataset, even when sample sizes and confidence levels match.
Degrees of freedom reflect the number of independent pieces of information available to estimate variability. When computing the sample standard deviation, one degree of freedom is lost because the sample mean is used in estimation.
This adjustment makes the t-distribution slightly wider for smaller samples, increasing the critical value and hence the margin of error.
Practice Questions
A random sample of 20 students has a sample mean revision time of 3.2 hours with a sample standard deviation of 0.9 hours.
A 95% confidence interval for the true mean revision time is to be constructed.
Explain how the margin of error for this interval is determined.
(1–3 marks)
Margin of error question (1–3 marks)
• 1 mark for stating that the margin of error is calculated using the critical value t* multiplied by the standard error (s divided by the square root of n).
• 1 mark for noting that t* depends on confidence level and degrees of freedom.
• 1 mark for recognising that the standard error uses the sample standard deviation because the population standard deviation is unknown.
(Max 3 marks)
A researcher collects data on the daily calcium intake (in milligrams) of a randomly selected sample of 15 adults. The sample mean is 845 mg, and the sample standard deviation is 120 mg. The researcher wishes to construct a 99% confidence interval for the population mean calcium intake.
(a) State and justify whether the t-distribution is appropriate for constructing the confidence interval.
(b) Explain how each of the following would affect the margin of error for this t-interval:
(i) increasing the sample size;
(ii) decreasing the confidence level;
(iii) the sample standard deviation being larger.
(4–6 marks)
Calcium intake question (4–6 marks)
(a)
• 1 mark for stating that the t-distribution is appropriate because the population standard deviation is unknown.
• 1 mark for stating that the sample size is small and thus requires the t-distribution.
• 1 mark for justifying that the sample must be approximately normal or show no strong skewness/outliers.
(b)
(i) Increasing sample size
• 1 mark for stating that increasing sample size reduces the standard error.
• 1 mark for concluding that this reduces the margin of error.
(ii) Decreasing confidence level
• 1 mark for noting that a lower confidence level leads to a smaller critical value t*.
• 1 mark for concluding that this decreases the margin of error.
(iii) Larger sample standard deviation
• 1 mark for stating that a larger standard deviation increases the standard error.
• 1 mark for concluding that this increases the margin of error.
(Max 6 marks)

