OCR Specification focus:
‘Perform calculations in mol involving mass, gas volume, solution volume and concentration; express concentration in mol dm–3 and g dm–3.’
Introduction
Mole calculations link measurable laboratory quantities—mass, gas volume and solution concentration—to the amount of substance. Understanding these relationships is essential for quantitative chemistry and accurate stoichiometric work.
The Mole in Quantitative Chemistry
The mole is central to all chemical calculations because it connects observable quantities with the number of particles involved in a chemical process. This subsubtopic focuses on applying mole relationships to solids, gases and solutions, ensuring students can calculate amounts of substance confidently across different contexts.
Amount of Substance in Solids: Mass and Moles
When dealing with solid substances, mass is the most common measurable quantity. Because each substance has its own molar mass, the numerical link between mass and amount of substance varies from compound to compound.
Molar Mass: The mass per mole of a substance, in g mol–1.
The ability to convert between mass and moles allows chemists to relate bulk material to particle-level quantities. This is particularly important when preparing reagents or determining stoichiometric ratios.
Using the Mass–Mole Relationship
The relationship between mass, molar mass and amount of substance is fundamental in this section. It allows students to calculate the number of moles in a given mass or determine the mass required to supply a specific molar amount.
Mass–Mole Relationship (n) = m ÷ M
n = amount of substance in mol
m = mass in g
M = molar mass in g mol–1
This relationship underpins stoichiometric calculations throughout A-Level Chemistry and directly supports the specification requirement to perform mole calculations involving mass.
For solids, using moles usually involves linking mass of a sample to its molar mass through the amount of substance.

This flowchart shows how mass, moles and number of particles interrelate, emphasising that mass–mole conversions depend on molar mass. It also includes particle-level relationships that extend slightly beyond the specification but reinforce the central role of the mole. Source
Moles in Gases: Gas Volumes and the Molar Gas Volume
For gaseous substances, volume rather than mass is usually measured. At a given temperature and pressure, equal volumes of gases contain equal numbers of molecules, enabling use of molar gas volume.
Molar Gas Volume: The volume occupied by one mole of a gas, usually 24 dm³ mol–1 at room temperature and pressure (RTP).
Gas volume calculations allow chemists to determine the amount of gaseous reactants or products from practical measurements. A clear understanding of molar gas volume is essential when interpreting gas collection experiments.
Applying Molar Gas Volume
Gaseous quantities can be converted to moles using a proportional relationship between volume and the molar gas volume. This is crucial for linking experimental measurements to stoichiometric analysis.
Gas Volume Relationship (n) = V ÷ Vm
n = amount of substance in mol
V = gas volume in dm³
Vm = molar gas volume in dm³ mol–1
This formula allows rapid conversion between experimentally collected gas volumes and molar quantities, aligning closely with the specification statement for gas calculations.
At room temperature and pressure, one mole of any gas occupies about 24.0 dm³, known as the molar gas volume, which lets us convert between moles and gas volume.

This schematic illustrates how moles link to mass and gas volume through molar mass and molar volume. The inclusion of particle relationships provides additional context beyond the syllabus but remains consistent with mole-based reasoning. Source
Moles in Solutions: Concentration, Volume and Amount of Substance
In reactions involving solutions, the measurable quantities are concentration and volume. The concentration of a solution expresses how much solute is present in a given volume of solvent and can be presented in mol dm–3 or g dm–3, both of which are required by the specification.
Concentration (mol dm–3): The amount of solute, in moles, dissolved per cubic decimetre of solution.
A firm grasp of concentration units ensures accurate preparation of solutions and correct interpretation of volumetric data.
Relating Concentration to Moles
The relationship between the concentration of a solution, its volume and the amount of substance of solute is a key quantitative link in titration and solution-based calculations.
Concentration Relationship (n) = c × V
n = amount of substance in mol
c = concentration in mol dm–3
V = volume in dm³
For solutions, the key relationship is between amount of solute in moles, solution volume in dm³, and concentration in mol dm–3.
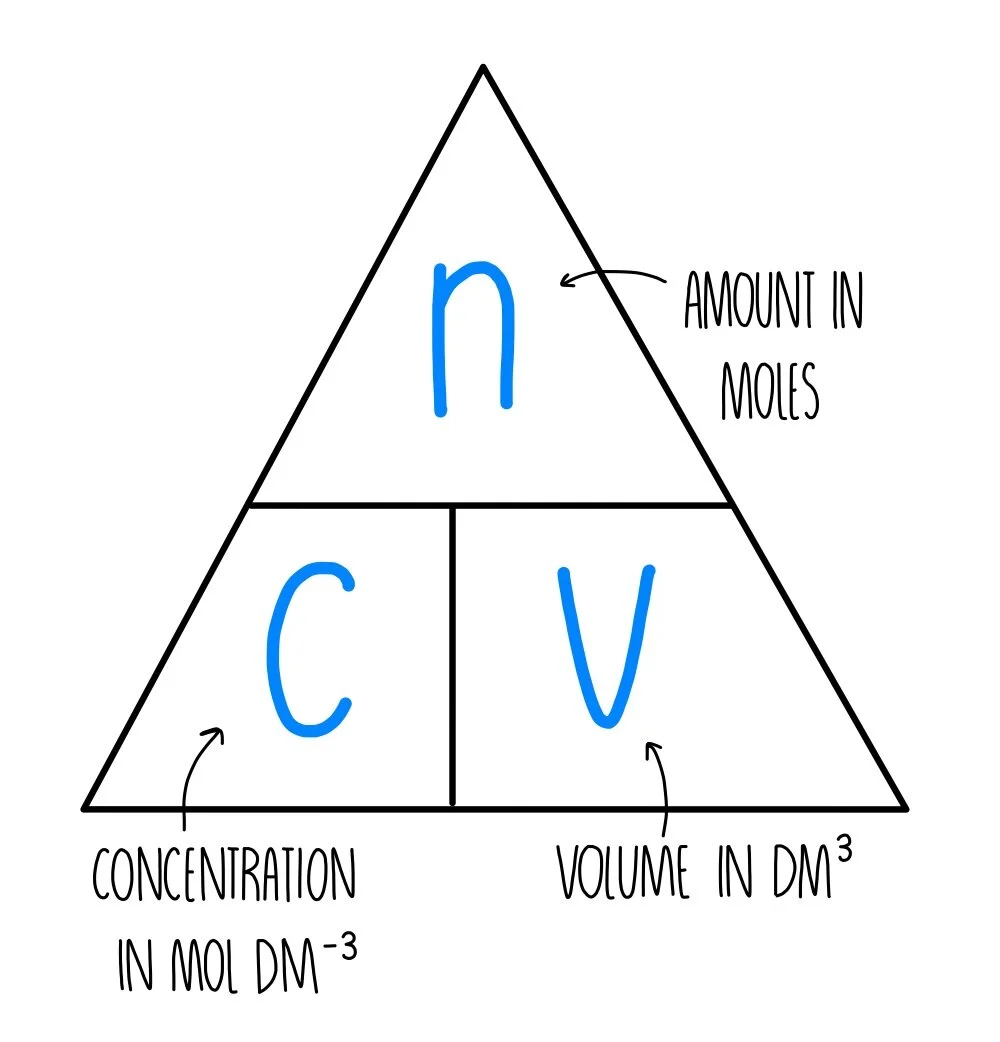
This triangle shows the relationship n = cV, with moles above and concentration and volume at the base. It provides a clear visual aid for rearranging the equation used in solution calculations. Source
This relationship forms the basis of nearly all calculations performed using titration data or volumetric analysis in aqueous chemistry.
Processes for Mole Calculations in Different Contexts
While calculations vary depending on whether solids, gases or solutions are involved, the underlying approach remains consistent. Students should be able to identify the type of data provided and select the correct relationship.
For Solids
Identify the mass of the substance.
Determine or calculate the molar mass.
Use the mass–mole relationship to calculate the amount of substance.
Link moles to chemical equations for stoichiometric analysis.
For Gases
Measure or determine the gas volume at known conditions.
Use the molar gas volume appropriate to the conditions.
Apply the gas volume relationship to calculate moles.
Connect moles to reaction equations where required.
For Solutions
Identify the volume and concentration of the solution.
Convert units to dm³ where necessary.
Use the concentration relationship to calculate moles of solute.
Connect mole values to stoichiometric relationships across the reaction.
Importance of Unit Consistency
Accurate mole calculations depend heavily on correct unit usage. Students must convert volumes to dm³, ensure molar masses are in g mol–1, and gas volumes match the specified dm³ mol–1 conditions. Misalignment of units is a frequent source of error in quantitative chemistry.
Integrating Stoichiometry
After calculating moles from mass, volume or concentration, students must apply stoichiometric principles to relate reactants and products. Stoichiometric coefficients in chemical equations indicate mole ratios, allowing prediction of product quantities or required reactant amounts. This integration of mole calculations with balanced equations is essential for mastering quantitative aspects of A-Level Chemistry and is directly aligned with the specification emphasis on mole-based calculations across multiple physical contexts.
FAQ
Identify the physical state and the type of data provided.
If the question gives a mass in grams, use the mass–mole relationship.
If a gas volume in dm³ is supplied at stated conditions, use the molar gas volume.
If concentration and solution volume are provided, use the concentration equation.
Choosing the correct starting point avoids unnecessary steps and reduces errors in multi-stage calculations.
The units in the concentration relationship must be consistent so that the calculation yields moles correctly. A concentration in mol dm–3 multiplied by a volume in cm³ would produce an incorrect unit, so converting ensures the operation aligns with the definition of concentration.
A quick conversion reminder: divide cm³ by 1000 to obtain dm³.
Students often forget that molar gas volume changes with temperature and pressure. If RTP is not specified, the value of 24.0 dm³ mol–1 may not apply.
Other frequent errors include:
Using cm³ instead of dm³
Applying significant figures inconsistently
Forgetting that the relationship assumes ideal gas behaviour
Uncertainties arise from balances, measuring cylinders, pipettes, and burettes. They affect the final calculated amount because each measured value contributes to overall percentage uncertainty.
To minimise errors:
Use apparatus with smaller measurement intervals
Weigh samples before and after transfer
Use volumetric equipment for solution work where possible
All three relationships are linear, meaning doubling one quantity doubles the others when the proportional variable remains constant. Recognising this makes it easier to estimate whether answers are reasonable.
It also supports multi-step reasoning, such as identifying limiting reagents or predicting how changing reactant amounts influences the amount of product formed.
Practice Questions
A student heats a sample of magnesium to produce magnesium oxide.
The mass of magnesium used is 0.60 g.
The molar mass of magnesium is 24.3 g mol–1.
Calculate the amount, in moles, of magnesium used.
Give your answer to two significant figures.
(2 marks)
Uses the relationship n = m / M. (1 mark)
Correct calculation: 0.60 / 24.3 = 0.0247 mol, rounded to 0.025 mol (2 s.f.). (1 mark)
Award full marks for 0.0247 mol or 0.025 mol.
A sample of nitrogen gas is collected over water at room temperature and pressure (RTP).
The volume of nitrogen collected is 2.40 dm³.
(a) Use the molar gas volume at RTP (24.0 dm³ mol–1) to calculate the amount, in moles, of nitrogen gas collected. (2 marks)
(b) The same amount of nitrogen gas is completely reacted to form nitrogen dioxide, NO2.
The equation for the reaction is:
N2(g) + 2O2(g) → 2NO2(g)
Calculate the volume, in dm³, of NO2 formed at RTP. (3 marks)
(5 marks)
(a)
Uses n = V / Vm. (1 mark)
Correct calculation: 2.40 / 24.0 = 0.100 mol. (1 mark)
(b)
Correct mole ratio from equation: N2 : NO2 is 1 : 2. (1 mark)
Calculates moles of NO2: 0.100 × 2 = 0.200 mol. (1 mark)
Uses V = n × Vm and calculates correct volume: 0.200 × 24.0 = 4.8 dm³. (1 mark)
Accept answers in the range 4.8 dm³ ± 0.1 dm³.

