Ideal gases allow chemists to link pressure, volume, temperature and amount of substance mathematically. Understanding how to use the ideal gas equation in correct SI units is essential for accurate quantitative gas calculations.

Ideal Gas Behaviour and the Role of SI Units

The ideal gas equation is a key quantitative relationship used across A-Level Chemistry. It provides a direct connection between measurable physical properties of a gas and the amount of substance, allowing chemists to determine unknown quantities under a wide range of conditions. Unlike models such as molar gas volume at room temperature and pressure, the ideal gas equation applies to any conditions provided values are converted correctly into SI units.

The equation assumes gases behave ideally, meaning their particles have negligible volume and experience no intermolecular forces. While real gases deviate, the approximation is sufficiently accurate for most calculations at temperatures well above their boiling points and at relatively low pressures.

The Ideal Gas Equation

The ideal gas equation combines four measurable variables and the gas constant into one expression that applies universally to ideal gases.

The equation is only valid when all quantities are expressed in correct SI units. This requirement forms the foundation of most common errors and is a major focus of the OCR specification.

A temperature value must always be converted into kelvin by adding 273 to the Celsius temperature. Similarly, pressures given in kilopascals, atmospheres or other units must be converted to pascals, and volumes such as cm³ or dm³ must be expressed in m³ before substitution.

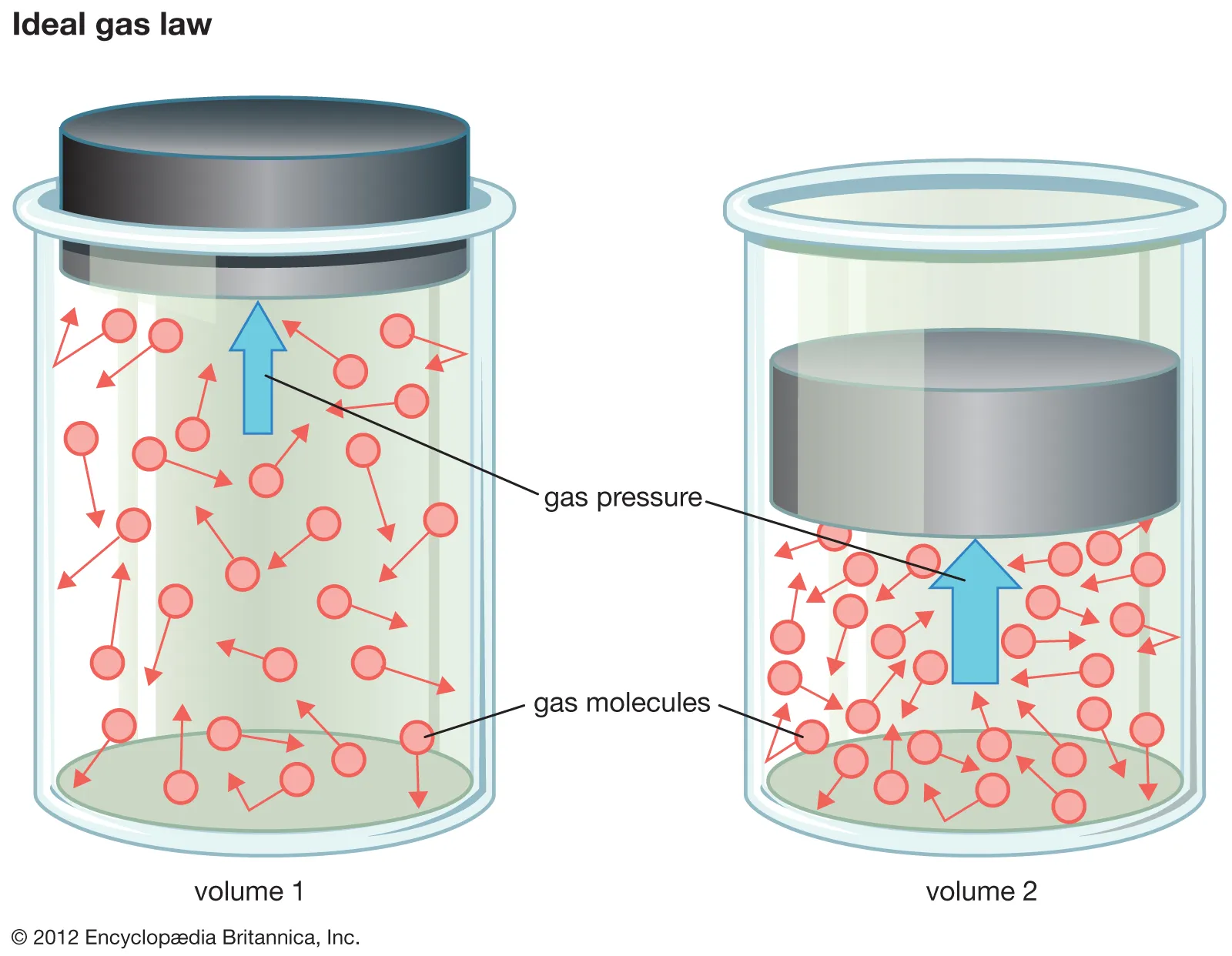
This diagram shows an ideal gas in a cylinder at two different volumes. As the piston compresses the gas, particle collisions become more frequent, increasing pressure. It visually represents the particle-level behaviour described by pV = nRT. Source

SI Unit Conversions Required for OCR

OCR A-Level Chemistry explicitly requires students to perform calculations using SI units, which ensures consistency and allows the ideal gas equation to be applied without modification. Key conversions include:

Temperature

Temperature must always be in kelvin (K), which is the SI base unit for temperature.

It is essential to convert temperatures before applying the equation, otherwise the proportional relationship between temperature and kinetic energy becomes invalid.

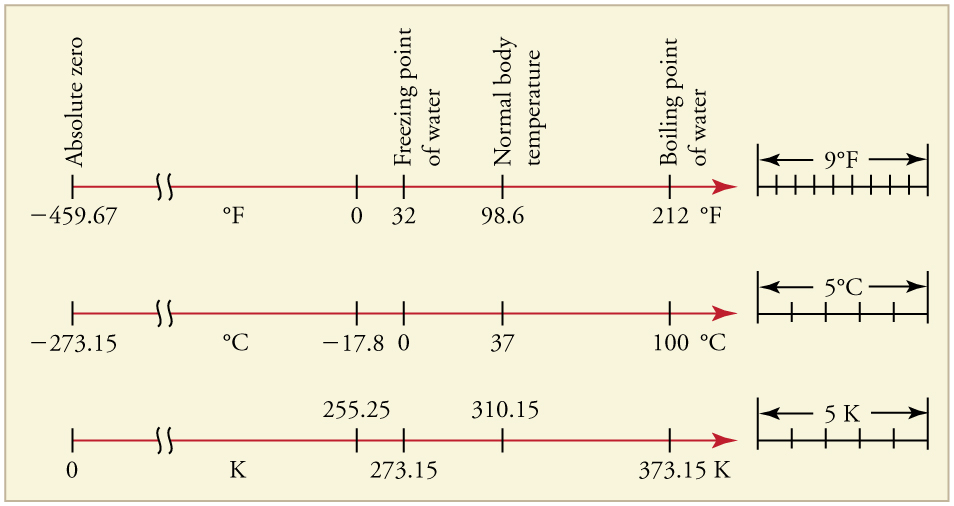
This figure compares Fahrenheit, Celsius, and Kelvin scales, showing freezing and boiling points of water. It highlights that Kelvin values are exactly 273.15 greater than Celsius values. Fahrenheit is included as additional context not required by OCR. Source

Pressure

Pressure must be measured in pascals (Pa).

Common conversions include:

• 1 kPa = 1,000 Pa

• 1 atm = 101,325 Pa

• 1 bar = 100,000 Pa

These units frequently appear in experimental data, so accurate conversion is fundamental for correct application of the ideal gas equation.

Volume

Volume must be expressed in cubic metres (m³).
Common conversions required by OCR include:

• 1 cm³ = 1 × 10⁻⁶ m³

• 1 dm³ = 1 × 10⁻³ m³

• 1 litre (L) = 1 × 10⁻³ m³

Students often need to convert from cm³ or dm³, particularly when working with apparatus such as gas syringes or volumetric flasks.

Understanding Each Variable in the Ideal Gas Equation

Each variable describes a measurable property of gas behaviour, and knowing how they interrelate helps in understanding the broader application of the equation.

Pressure (p)

Pressure represents the force per unit area exerted by gas particles colliding with the walls of a container. In the context of the ideal gas equation, pressure must be in Pa, reflecting the SI definition of force and area.

Volume (V)

Volume refers to the space occupied by the gas. Using volume in m³ ensures compatibility with the joule-based units of the gas constant R.

Amount of Substance (n)

The amount of substance links microscopic particles to macroscopic measurements. When combined with Avogadro’s constant, it enables chemists to relate molar quantities to particle behaviour.

Temperature (T)

Temperature in kelvin is directly proportional to the average kinetic energy of gas particles. This proportionality underpins the behaviour predicted by the ideal gas model.

The Gas Constant (R)

The constant R ensures the relationship between p, V, n, and T is numerically consistent. OCR provides its value (8.314 J mol⁻¹ K⁻¹) on the Data Sheet during examinations.

Practical Application of the Ideal Gas Equation

To apply the ideal gas equation accurately in OCR A-Level Chemistry, students must integrate multiple skills:

Required Process for Using the Ideal Gas Equation

• Convert all quantities to SI units: Pa, m³, K, mol

• Check that the temperature conversion to kelvin is completed before rearranging

• Identify the unknown variable required by the question

• Rearrange the equation algebraically into the appropriate form

• Substitute the values and evaluate using consistent significant figures

This structured approach ensures alignment with specification expectations.

Recognising When to Use the Ideal Gas Equation

The ideal gas equation is particularly useful when conditions differ from standard temperature and pressure or when the molar gas volume relationship (24 dm³ mol⁻¹ at RTP) does not apply. Typical situations include:

• Gases collected in experiments involving heating or compression

• Calculations involving gas-producing reactions

• Determining unknown molar amounts from physical measurements

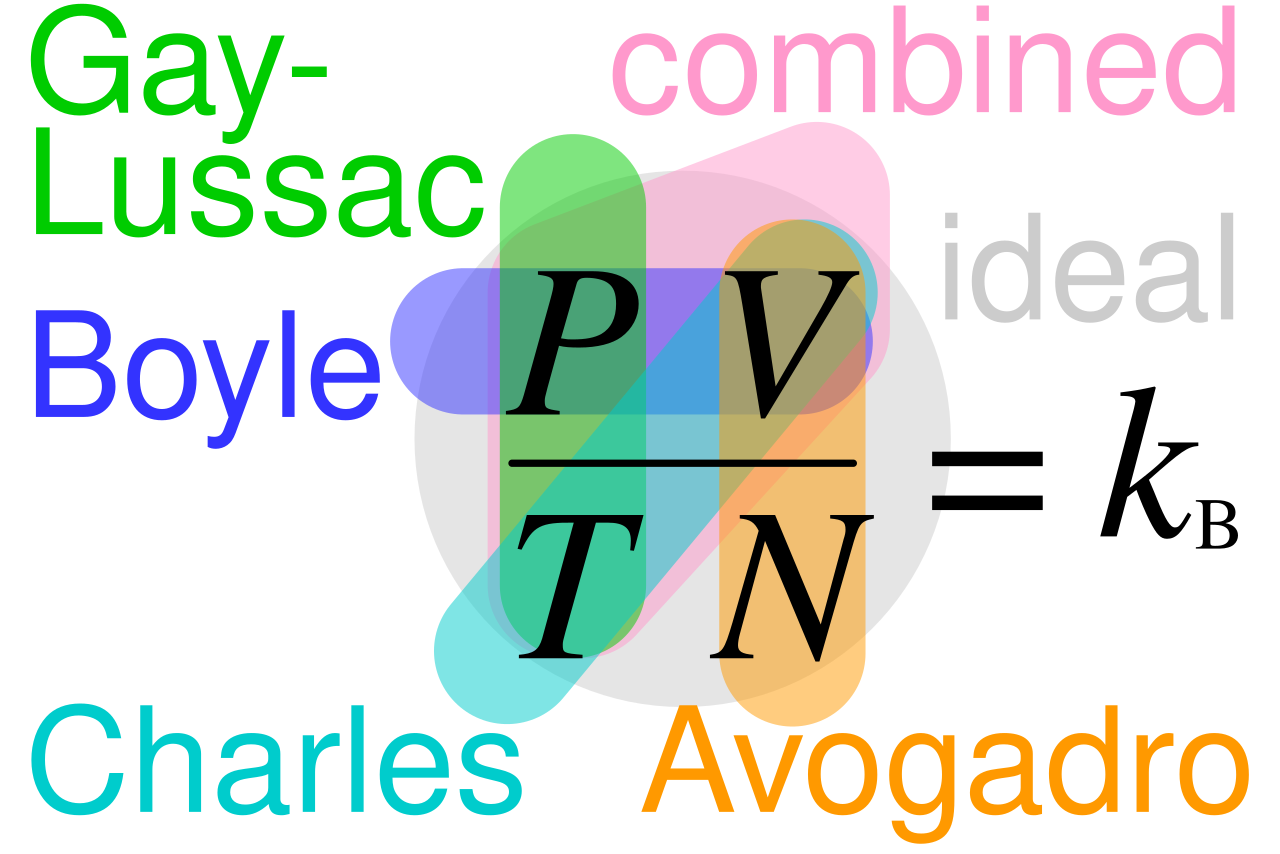
This diagram summarises how the simple gas laws connect to the ideal gas equation pV = nRT. Each arrow indicates conditions held constant and variables that change. The named gas laws provide helpful context beyond the core OCR requirement. Source

Limitations of the Ideal Gas Model

Although the equation assumes ideal behaviour, real gases show deviations at high pressures and low temperatures. OCR expects students to recognise that:

• Intermolecular forces reduce pressure compared to ideal predictions

• Particle volume becomes significant at high pressures

These deviations explain why the ideal gas equation is an approximation, but for most A-Level contexts it remains sufficiently accurate, provided units are correctly assigned.