OCR Specification focus:
‘Define Ka and pKa; use pH = −log[H⁺] and Kw to relate [H⁺] and [OH⁻].’
This section introduces quantitative measures of acidity, explaining equilibrium expressions for acids, logarithmic pH scales, and the ionic product of water, Kw.
Acidity, Equilibrium and Quantification
Acids in aqueous solution establish equilibria rather than fully reacting, except in the case of strong acids. To compare acid strengths and calculate pH values accurately, chemists use equilibrium constants and logarithmic scales. These tools allow acidity to be expressed numerically and consistently across a wide range of concentrations.
Understanding Ka, pKa, pH, and Kw provides the foundation for later pH calculations, buffer chemistry, and titration analysis. Each quantity is rooted in equilibrium principles and reflects the extent to which acids and water ionise in solution.
Acid Dissociation Constant, Ka
Weak acids partially dissociate in water, forming an equilibrium between the undissociated acid and its ions. This equilibrium is quantified using the acid dissociation constant.
Ka: The equilibrium constant for the dissociation of a weak acid in aqueous solution, showing the extent of ionisation.
For a generic weak acid, HA, the dissociation can be represented as: HA(aq) + H₂O(l) ⇌ H⁺(aq) + A⁻(aq)
This diagram illustrates the equilibrium dissociation of a weak acid in water, forming its conjugate base and hydronium ions. It supports the definition of Ka as an equilibrium constant based on dissolved species. The structural formulae shown go beyond the minimum required by the syllabus. Source
Only aqueous species appear in the equilibrium expression, as liquids have constant concentration.
Acid dissociation constant (Ka) = [H⁺][A⁻] / [HA]
[H⁺] = Equilibrium concentration of hydrogen ions (mol dm⁻³)
[A⁻] = Equilibrium concentration of conjugate base ions (mol dm⁻³)
[HA] = Equilibrium concentration of undissociated acid (mol dm⁻³)
A larger Ka value indicates a greater extent of dissociation and therefore a stronger weak acid. Very small Ka values correspond to very weak acids that dissociate only slightly in water.
The pKa Scale
Because Ka values often span several orders of magnitude, they are commonly expressed using a logarithmic scale known as pKa.
pKa: The negative logarithm (base 10) of the acid dissociation constant, Ka.
The pKa scale simplifies comparison between acids and avoids the use of very small numbers. A lower pKa corresponds to a stronger acid, while a higher pKa indicates a weaker acid.
The logarithmic nature of pKa means:
A decrease of 1 unit in pKa represents a tenfold increase in Ka
Acids with similar pKa values have similar strengths
pKa values are temperature-dependent because they are derived from Ka, which itself varies with temperature.
Definition and Meaning of pH
The acidity of a solution is expressed using pH, which relates directly to the concentration of hydrogen ions present.
pH: A logarithmic measure of the hydrogen ion concentration in aqueous solution.
pH = −log[H⁺]
[H⁺] = Hydrogen ion concentration in mol dm⁻³
The pH scale is logarithmic:
A decrease of 1 pH unit corresponds to a tenfold increase in [H⁺]
Lower pH values indicate more acidic solutions
Higher pH values indicate more alkaline solutions
This definition applies to all aqueous solutions, including acids, bases, and neutral water.
Ionic Product of Water, Kw
Pure water undergoes slight self-ionisation, producing equal concentrations of hydrogen and hydroxide ions. This equilibrium is described by Kw.
Kw: The ionic product of water, equal to the product of hydrogen and hydroxide ion concentrations at a given temperature.
Kw = [H⁺][OH⁻]
[H⁺] = Hydrogen ion concentration (mol dm⁻³)
[OH⁻] = Hydroxide ion concentration (mol dm⁻³)
At 25 °C, Kw has a value of 1.0 × 10⁻¹⁴ mol² dm⁻⁶. This value is constant at a fixed temperature but increases as temperature rises.
In neutral water:
[H⁺] = [OH⁻] = 1.0 × 10⁻⁷ mol dm⁻³
pH = 7
Relationship Between pH and pOH
Using Kw, hydrogen and hydroxide ion concentrations are directly linked. This allows pH and pOH to be related mathematically.
From Kw:
If [H⁺] increases, [OH⁻] must decrease
If [OH⁻] increases, [H⁺] must decrease
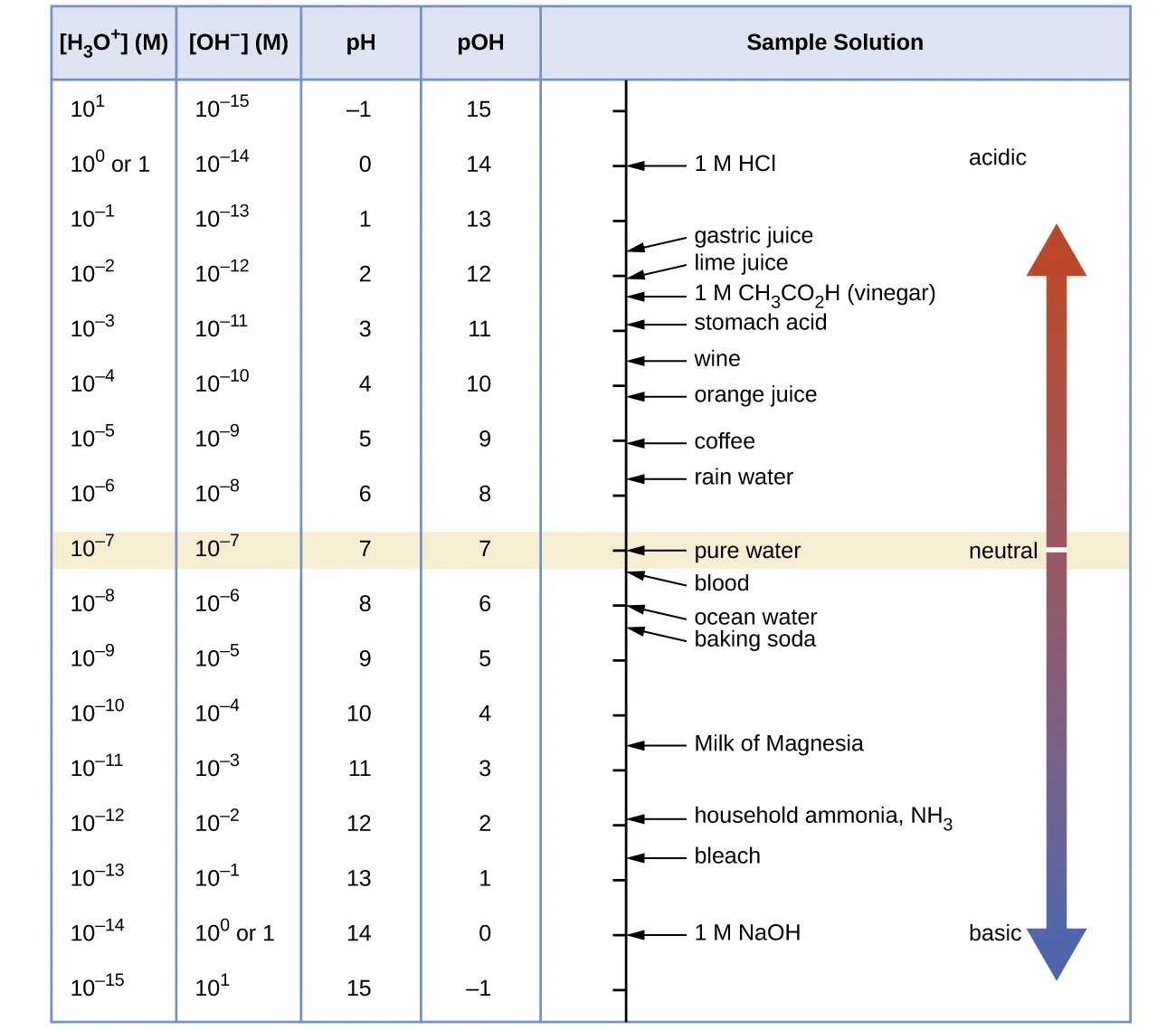
This chart shows the logarithmic pH scale and the inverse relationship between hydrogen and hydroxide ion concentrations implied by Kw. It reinforces how changes in [H⁺] correspond to changes in [OH⁻]. The inclusion of pOH and example substances extends beyond the OCR syllabus but provides helpful context. Source
This relationship underpins calculations involving strong bases, where hydroxide concentration is often known first. It also reinforces that all aqueous solutions contain both H⁺ and OH⁻ ions, even if one is present in much lower concentration.
Connecting Ka, pKa, and pH
Ka and pKa describe acid strength, while pH describes solution acidity. These quantities are linked but not interchangeable:
Ka and pKa are constants for a given acid at a fixed temperature
pH depends on acid concentration as well as acid strength
For weak acids, pH reflects the position of the dissociation equilibrium described by Ka. Strong acids, by contrast, dissociate fully and do not require Ka values for pH determination.
Together, Ka, pKa, pH, and Kw provide a coherent framework for understanding acidity, alkalinity, and equilibrium behaviour in aqueous chemistry at A-Level standard.
FAQ
Strong acids dissociate completely in aqueous solution, meaning no equilibrium exists between undissociated acid and ions.
Ka relies on a measurable equilibrium position. For strong acids, the concentration of undissociated acid is effectively zero, making Ka values impractical and meaningless at A-Level.
Ka and Kw are both temperature-dependent equilibrium constants.
Increasing temperature generally increases Kw because water ionisation is endothermic
Ka may increase or decrease depending on whether acid dissociation is endothermic or exothermic
As pKa is derived from Ka, any temperature change that affects Ka will also change pKa.
pH compresses a very wide range of hydrogen ion concentrations into a manageable numerical scale.
A logarithmic scale allows:
Easy comparison of very acidic and very dilute solutions
Clear expression of tenfold changes in acidity per pH unit
This makes pH practical for laboratory use and chemical analysis.
Water undergoes continuous self-ionisation due to molecular collisions.
At any moment:
Some water molecules donate protons
Others accept protons
This dynamic equilibrium produces equal concentrations of H⁺ and OH⁻, even in pure water, explaining why Kw is never zero.
Neutrality depends on equal concentrations of H⁺ and OH⁻, not a fixed pH value.
As temperature increases:
Kw increases
Both [H⁺] and [OH⁻] increase equally
This can result in neutral solutions having a pH below 7, even though they are not acidic.
Practice Questions
Define the terms Ka and pH as used in aqueous acid–base chemistry.
(2 marks)
Award marks as follows:
1 mark for defining Ka as the equilibrium constant for the dissociation of a weak acid in aqueous solution, showing the extent of ionisation.
1 mark for defining pH as the negative logarithm (base 10) of the hydrogen ion concentration.
Explain how the ionic product of water, Kw, links the concentrations of hydrogen ions and hydroxide ions in aqueous solutions. In your answer, refer to neutral, acidic, and alkaline solutions and the relationship to pH.
(5 marks)
Award marks as follows:
1 mark for stating that Kw is defined as the product of the hydrogen ion concentration and hydroxide ion concentration, Kw = [H+][OH−].
1 mark for stating that Kw has a constant value at a fixed temperature.
1 mark for explaining that in neutral water, [H+] equals [OH−].
1 mark for explaining that in acidic solutions [H+] is greater than [OH−].
1 mark for explaining that in alkaline solutions [OH−] is greater than [H+], or for correctly linking these relationships to changes in pH.
Maximum 5 marks.

