These notes explain how to calculate pH for strong acids, strong bases, and weak acids, focusing on assumptions, equilibrium ideas, and syllabus-specific chemical reasoning.

Understanding pH and Hydrogen Ion Concentration

pH calculations are central to acid–base chemistry because they quantify acidity and alkalinity using hydrogen ion concentration. All pH calculations ultimately depend on the relationship between [H⁺], [OH⁻], and water equilibrium.

pH is first introduced as a logarithmic measure of hydrogen ion concentration, allowing very large concentration ranges to be handled conveniently.

The logarithmic nature of pH means that small numerical changes correspond to large chemical differences. Accurate identification of [H⁺] is therefore essential before calculating pH.

Strong Acids and pH Calculations

Strong acids are characterised by complete dissociation in aqueous solution. This means that every acid molecule donates a proton to water, making pH calculations relatively direct.

For a monoprotic strong acid, the hydrogen ion concentration equals the acid concentration because dissociation is complete. No equilibrium expression is required.

For strong acids and strong bases, assume complete dissociation, so the acid or base concentration directly gives [H⁺] or [OH⁻].

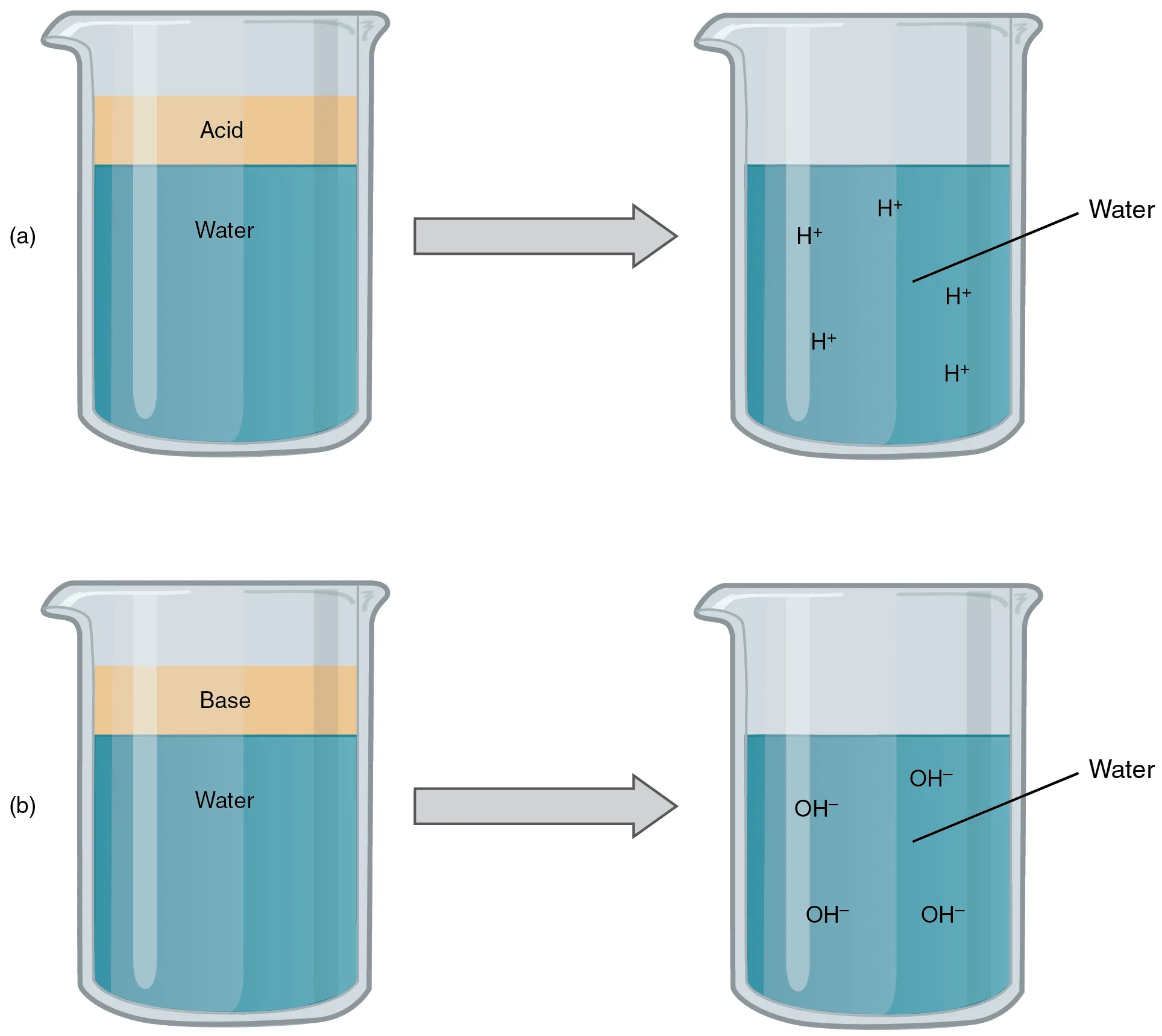
This diagram shows that a strong acid dissociates almost completely to give a high concentration of H⁺, while a strong base dissociates almost completely to give a high concentration of OH⁻. This supports the direct approach used for strong acid and strong base pH calculations. Source

Important features when calculating pH of strong acids include:

• Complete ionisation, so no equilibrium assumption is needed

• Stoichiometric relationships determine [H⁺]

• Water auto-ionisation is negligible compared with acid contribution

When dealing with polyprotic strong acids, the number of protons released per molecule must be considered, as this directly affects [H⁺].

Strong Bases and the Use of Kw

Strong bases fully dissociate to produce hydroxide ions rather than hydrogen ions. Because pH depends on [H⁺], the ionic product of water must be used.

The link between hydroxide ions and hydrogen ions is defined by the ionic product of water.

Kw links [H⁺] and [OH⁻] in all aqueous solutions, because water establishes an equilibrium between H₃O⁺ and OH⁻.

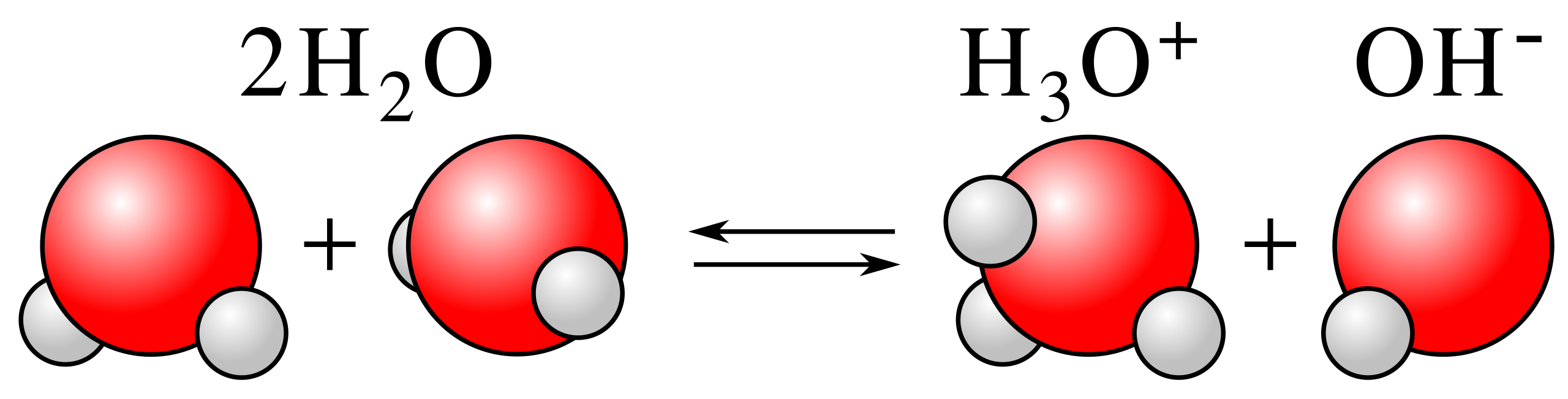
This diagram illustrates the self-ionisation of water, forming hydronium and hydroxide ions. It explains why Kw can be used to convert between [OH⁻] and [H⁺] when calculating pH for strong bases. Source

Using Kw allows conversion between [OH⁻] and [H⁺]. This step is essential before applying the pH definition. Temperature dependence of Kw is not required here, as calculations assume standard conditions unless stated otherwise.

Key points for strong base calculations:

• Determine [OH⁻] from base dissociation

• Use Kw to calculate [H⁺]

• Apply the pH definition only after finding [H⁺]

Weak Acids and Equilibrium Considerations

Weak acids only partially dissociate in aqueous solution, so equilibrium ideas must be applied. Unlike strong acids, hydrogen ion concentration is not equal to the initial acid concentration.

Weak acid dissociation is described using an equilibrium constant, Ka, which measures the extent of ionisation.

Weak acids only partially ionise, so pH is found from an equilibrium using Ka rather than assuming [H⁺] equals the initial acid concentration.

This figure shows a weak acid establishing an equilibrium with water. Although acetic acid is used as the example, it represents the general HA ⇌ H⁺ + A⁻ behaviour applied in weak-acid pH calculations. Source

Approximations in Weak Acid pH Calculations

For many weak acids, dissociation is minimal. This allows simplifying assumptions that make pH calculations manageable without solving complex equations.

The common approximation used is:

• [HA] ≈ initial acid concentration

• [H⁺] ≈ [A⁻]

These assumptions are valid when the acid is weak and the equilibrium lies far to the left. They allow Ka expressions to be rearranged to estimate [H⁺] directly.

Conditions supporting valid approximations include:

• Small Ka values

• Relatively high initial acid concentrations

• Minimal percentage dissociation

The specification requires recognising and using these approximations appropriately, without extending into situations where they break down.

Comparing Strong and Weak Acid Calculations

Strong and weak acid pH calculations differ fundamentally in approach, even when starting concentrations appear similar.

Key contrasts include:

• Strong acids: complete dissociation, no equilibrium calculation

• Weak acids: partial dissociation, Ka expression required

• Hydrogen ion source: direct for strong acids, equilibrium-controlled for weak acids

Understanding these differences ensures correct method selection, which is essential for accurate pH determination at A-Level standard.

Linking pH Calculations to Chemical Reasoning

pH calculations are not purely mathematical; they reflect underlying chemical behaviour. Recognising whether an acid or base is strong or weak determines whether equilibrium reasoning or direct stoichiometry is appropriate.

Throughout this topic, careful identification of:

• Degree of dissociation

• Relevant equilibrium constants

• Valid approximations

ensures that pH calculations remain chemically meaningful and fully aligned with OCR A-Level Chemistry expectations.