Investigating I–V characteristics allows physicists to understand how current and potential difference relate in components. Practical experiments provide quantitative data to identify ohmic and non-ohmic behaviour precisely.

Understanding I–V Characteristics

Definition and Context

Each component has its own unique I–V characteristic that depends on its material, temperature, and structure. Analysing these relationships helps distinguish between ohmic conductors, where current is proportional to potential difference, and non-ohmic devices, where the relationship is nonlinear.

Accurate measurement and analysis of these characteristics are crucial for designing and understanding electronic circuits.

Setting Up an I–V Experiment

Apparatus Required

An investigation into I–V characteristics typically uses the following equipment:

• DC power supply (adjustable output)

• Ammeter (to measure current through the component)

• Voltmeter (to measure potential difference across the component)

• Variable resistor (to vary current systematically)

• Connecting wires and switch

• Component under test, e.g. a resistor, filament lamp, thermistor, or diode

The aim is to measure I for a range of applied V values, ensuring accurate readings for both increasing and decreasing currents to detect hysteresis or thermal effects.

Circuit Arrangement

The circuit must be built according to standard electrical conventions:

• The ammeter is connected in series with the component.

• The voltmeter is connected in parallel across it.

• The variable resistor allows smooth control of the current.

• A switch ensures the circuit is only energised during measurements to avoid heating effects.

Before connecting, verify the circuit using a circuit diagram, drawn with correct standard symbols and neat, straight lines for clarity.

Data Collection Procedure

Step-by-Step Process

1. Set up the circuit correctly on a low voltage setting to ensure safety.

2. Close the switch and adjust the variable resistor to obtain a small current.

3. Record the readings of voltage and current.

4. Increase the current in small, equal increments, taking corresponding voltage readings.

5. Reverse the polarity of the power supply to obtain values for negative voltages if required.

6. Repeat the measurements to reduce random errors and obtain a mean.

7. Allow components to cool between runs, especially for non-ohmic devices sensitive to temperature.

When recording data, tabulate results clearly with appropriate units (volts, amperes). Maintaining consistent precision in measurements (e.g., two decimal places) ensures data reliability.

Ensuring Accuracy and Reducing Error

Measurement Accuracy

Accurate I–V data depend on careful experimental technique:

• Use digital meters for precise readings.

• Minimise contact resistance by using clean connections.

• Use short, thick wires to reduce internal resistance effects.

• Avoid heating the component, as temperature changes alter resistance.

• Repeat and average readings to mitigate random error.

Systematic errors can be reduced by checking meter calibration and ensuring that the zero offsets of instruments are corrected before beginning.

Risk Management

To manage experimental risk:

• Never exceed the maximum current rating of the component.

• Keep the circuit energised only briefly for each measurement.

• Disconnect power between adjustments.

• Handle diodes and LEDs carefully to avoid damage from reverse bias.

Good practice ensures the experiment is both safe and scientifically valid.

Analysing the Data

Graphical Analysis

Once data are collected, plot a graph of V (x-axis) against I (y-axis) to visualise the component’s characteristic. Each device type displays distinctive behaviour:

• Ohmic resistor: Straight line through the origin; current ∝ voltage.

• Filament lamp: Curved line; resistance increases with temperature.

• Diode: No current until threshold voltage; sharp rise thereafter.

• Thermistor: Non-linear; resistance decreases as temperature rises.

The gradient of the line (ΔV/ΔI) gives the resistance (R) at any point.

EQUATION
—-----------------------------------------------------------------
Resistance (R) = V ÷ I
V = Potential difference across the component (volts, V)
I = Current through the component (amperes, A)
R = Resistance (ohms, Ω)
—-----------------------------------------------------------------

For non-linear graphs, the resistance is not constant but varies with applied voltage or current. The concept of dynamic resistance (local gradient) is particularly useful for semiconductors.

Plot current on the y-axis against potential difference on the x-axis to obtain the component’s I–V characteristic, then describe the curve’s shape.

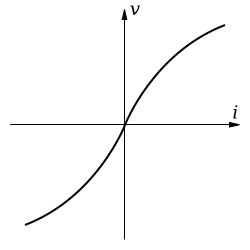
Non-ohmic I–V characteristic illustrating how the gradient decreases as current rises, consistent with thermal increase of resistance. This mirrors the filament lamp curve students obtain in practice. The graphic is intentionally simple and avoids extraneous annotation. Source.

Using Spreadsheets for Analysis

Modern investigations use spreadsheets to enhance precision and analysis:

• Input all recorded values of V and I.

• Calculate R = V/I for each data point automatically.

• Plot I–V graphs using scatter plots with trendlines.

• Determine gradients for different regions to examine changing resistance.

• Include uncertainty bars or error columns to assess measurement reliability.

Spreadsheets also simplify comparison between components, allowing clear identification of ohmic vs non-ohmic behaviour.

Evaluating Uncertainties

Experimental Uncertainty

Each measurement has inherent uncertainty due to instrument limitations and environmental conditions. For digital meters:

• Uncertainty ≈ ± one least significant digit of the display.

• For analogue meters, use ± half a division rule.

Uncertainty in resistance derived from V and I can be estimated by combining fractional uncertainties:

EQUATION
—-----------------------------------------------------------------
Fractional Uncertainty in R = (ΔV/V) + (ΔI/I)
ΔV = Uncertainty in voltage (volts)
ΔI = Uncertainty in current (amperes)
R = Calculated resistance (ohms)
—-----------------------------------------------------------------

These estimates help to judge whether apparent variations in results are significant or within experimental tolerance.

Reliability and Reproducibility

High-quality data should show consistent patterns across repeated trials. If results deviate, consider factors such as:

• Temperature change during measurements.

• Inaccurate zeroing of meters.

• Loose connections causing intermittent readings.

Re-testing under controlled conditions ensures reproducibility, strengthening the validity of conclusions.

Interpreting Findings

Understanding Component Behaviour

Analysing I–V curves allows students to:

• Identify ohmic conductors (constant R).

• Recognise non-ohmic behaviour in components affected by temperature, light, or material structure.

• Understand the microscopic mechanisms, e.g. heating in metals or charge carrier behaviour in semiconductors.

Such practical investigations reinforce theoretical models and prepare students for quantitative problem solving in further circuit analysis.

For the diode, take readings in forward and reverse bias, limiting current with a series resistor, and plot the characteristic.

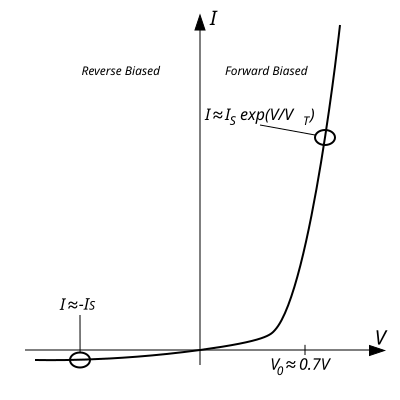
Diode I–V curve showing negligible reverse current, a forward threshold, and distinct operating regions. This clarifies why data look asymmetric when polarity is reversed. Note: the graphic includes labelled regions (e.g., “breakdown”) which extend slightly beyond the minimum syllabus requirement but aid interpretation. Source.