OCR Specification focus:
‘Define interference, coherence, path difference, and phase difference for two waves.’
Waves interact in fascinating ways, producing effects that form the foundation of modern optics and acoustics. Understanding interference, coherence, path difference, and phase difference explains how wave overlap creates distinct, observable patterns in light, sound, and microwaves.
Interference of Waves
When two or more progressive waves of the same type meet, they superpose, meaning their displacements combine at each point in space and time. This interaction can reinforce or cancel the overall displacement, leading to interference patterns.
Interference: The phenomenon that occurs when two or more waves overlap, and the resultant displacement at each point is the vector sum of the individual displacements.
Interference demonstrates that waves are not isolated events but dynamic interactions. In optics and acoustics, this principle explains phenomena such as light fringes, sound beats, and the patterns observed in the Young double-slit experiment.
There are two main forms of interference:
Constructive interference – occurs when waves meet in phase, leading to an increase in amplitude.
Destructive interference – occurs when waves meet out of phase, reducing or completely cancelling amplitude.
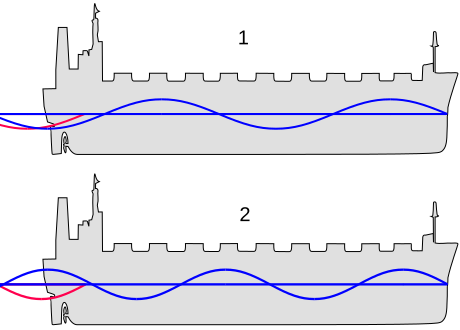
When two waves of equal frequency superpose in phase, amplitudes add to give constructive interference (left). With a phase difference of 180° (π radians), amplitudes cancel to give destructive interference (right). This diagram directly illustrates the superposition principle for two coherent waves. Source.
For interference to be sustained and observable, the waves must maintain a stable phase relationship over time. This brings us to the concept of coherence.
Coherence and Its Importance
Coherence: A property of two or more waves that have a constant phase difference and the same frequency, allowing sustained interference patterns to form.
In practical terms, coherence determines whether interference is visible or not. Two light sources, for instance, rarely show stable interference because their emitted waves fluctuate randomly in phase. However, if both sources originate from the same parent wave (as in a double-slit experiment), they are coherent.
Types of Coherence
Temporal coherence: Measures how consistent the phase relationship remains over time. It depends on the wavelength range (or spectral purity) of the source. A monochromatic laser has high temporal coherence.
Spatial coherence: Describes how uniform the phase is across the wavefront at a given instant. Sources with small emission areas, like lasers, tend to exhibit high spatial coherence.
Without coherence, interference fringes fade and no stable pattern emerges.
Path Difference
Path Difference: The difference in distance travelled by two waves from their respective sources to a common point of observation.
When waves from two coherent sources travel different distances before meeting, the extra distance one travels affects whether they interfere constructively or destructively.
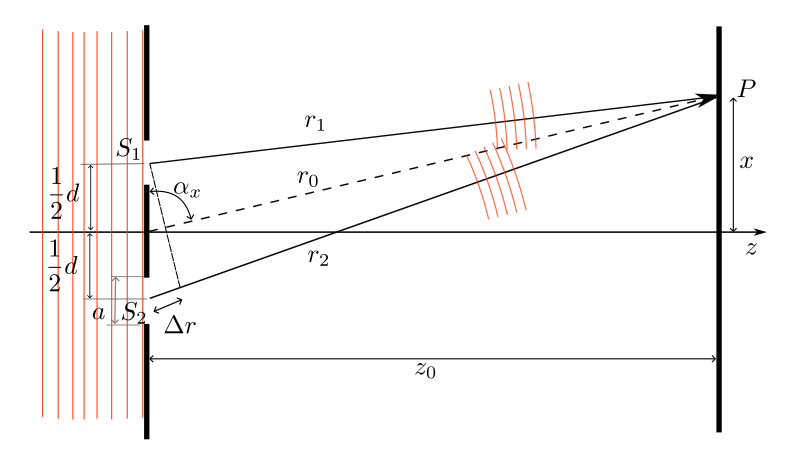
Labeled double-slit geometry showing two coherent rays from slits to a screen point with path lengths and Δx. Positions of constructive (Δx = nλ) and destructive (Δx = (n+½)λ) interference follow from this layout. Extra variables for slit separation and screen distance are included to clarify the geometry; they are supportive but not strictly required by the OCR subsubtopic. Source.
EQUATION
—-----------------------------------------------------------------
Path Difference (Δx) = nλ or (n + ½)λ
Δx = difference in path length (metres, m)
λ = wavelength of the waves (metres, m)
n = integer representing the order of interference
—-----------------------------------------------------------------
Constructive interference occurs when the path difference equals an integer multiple of the wavelength:
Δx = nλDestructive interference occurs when the path difference equals an odd multiple of half a wavelength:
Δx = (n + ½)λ
For example, at points where two coherent light waves meet with a path difference of exactly one wavelength, bright fringes form. Where the difference is half a wavelength, dark fringes appear.
Phase Difference
Phase Difference: The fraction of a wave cycle by which one wave is ahead or behind another, expressed in degrees (°) or radians (rad).
The phase difference indicates how much one wave’s oscillation leads or lags relative to another’s.
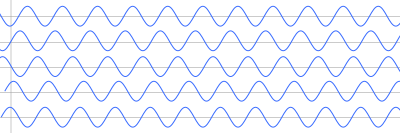
Set of sine waves of the same frequency with different phase differences (e.g. 0°, 90°, 180°). A constant horizontal shift represents phase lead/lag, which determines whether superposition is constructive, destructive, or intermediate. The figure is minimalist and directly aligned with the OCR definitions. Source.
EQUATION
—-----------------------------------------------------------------
Phase Difference (ϕ) = (2πΔx) / λ
ϕ = phase difference (radians, rad)
Δx = path difference (metres, m)
λ = wavelength (metres, m)
—-----------------------------------------------------------------
When two waves have a phase difference of:
0 or multiples of 2π radians, they are in phase, producing constructive interference.
π radians (180°), they are out of phase, producing destructive interference.
This equation establishes a direct quantitative relationship between path difference and phase difference, enabling accurate prediction of interference effects.
Relationship Between Interference, Coherence, Path, and Phase Difference
Interference patterns rely on a delicate balance among these four principles:
Interference is the visible manifestation of wave superposition.
Coherence ensures that the phase relationship between waves remains fixed, making patterns stable over time.
Path difference determines where on a screen or in space constructive and destructive interference occur.
Phase difference translates the physical path difference into a measurable angular displacement within the wave cycle.
These quantities are interdependent — coherence allows meaningful phase and path comparisons, and interference emerges as their observable consequence.
Conditions for Stable Interference Patterns
For two sources (such as slits, speakers, or microwave emitters) to produce a clear interference pattern, the following conditions must be met:
The sources must emit waves of the same frequency and wavelength.
The sources must be coherent, maintaining a constant phase difference.
The waves must have the same type of polarisation (for electromagnetic waves).
The amplitudes should be comparable to create visible contrast between maxima and minima.
The path difference must be small relative to the coherence length of the source.
Meeting these conditions ensures stable, well-defined interference fringes that can be measured and analysed in laboratory or experimental contexts.
Applications Across the Spectrum
The principles of interference are central to understanding modern wave-based technologies and experiments:
Optics: Interference underlies thin-film colours, anti-reflective coatings, and the Michelson interferometer.
Acoustics: Interference produces beats and is used to measure sound wavelengths.
Microwaves: Laboratory setups with coherent microwave sources visually demonstrate superposition and interference fringes.
Each application showcases how precise relationships among path, phase, and coherence reveal the wave nature of energy propagation.
FAQ
Fringes fade when the waves lose coherence — that is, when the phase relationship between them becomes unstable.
This can happen because:
The sources are not truly coherent (different frequencies or fluctuating phases).
Environmental disturbances, such as vibrations or air currents, alter the path lengths.
Variations in temperature or pressure affect the refractive index of air, changing wave speed and phase.
Maintaining stable conditions and using a single coherent source (e.g. a laser) helps preserve a visible interference pattern.
If one wave’s amplitude is much greater than the other’s, the resultant displacement barely fluctuates, and interference effects become weak.
Constructive interference increases total amplitude, but destructive interference never fully cancels the stronger wave, making bright and dark fringes less distinct.
For maximum contrast, both waves should have similar amplitudes so that constructive regions appear bright and destructive regions appear dark.
Coherence length is the maximum path difference over which waves maintain a fixed phase relationship.
If the path difference exceeds this length, interference fringes blur or disappear.
For monochromatic light, coherence length depends on spectral purity — lasers have very long coherence lengths (metres or more), while ordinary lamps have much shorter ones (micrometres).
Ensuring path differences are smaller than the coherence length is crucial for clear interference patterns.
Yes, but it produces a varying or “beating” pattern rather than a stationary interference pattern.
When two waves have slightly different frequencies:
Their constructive and destructive interference alternates over time.
The resulting amplitude fluctuates at a frequency equal to the difference between the two wave frequencies (the beat frequency).
This is often used in acoustics to tune instruments but does not form the steady spatial interference pattern seen with coherent light or microwaves.
Two separate light bulbs emit light with random and independent phase changes due to their many independent atomic emissions.
As a result, the phase difference between their emitted waves fluctuates rapidly, destroying any stable interference pattern.
In contrast, coherent sources (e.g. two slits from one laser beam) share a single origin, so their phase difference remains constant, allowing observable interference fringes to form.
Practice Questions
Question 1 (2 marks)
Two coherent sound waves of the same frequency arrive at a point in space with a phase difference of 180°.
(a) State the term used to describe this type of interference.
(b) Describe the resultant effect on the sound intensity at that point.
Mark scheme:
(a) Destructive interference – 1 mark
(b) Waves are out of phase and cancel each other, producing a minimum or zero sound intensity – 1 mark
Question 2 (5 marks)
Light from a single laser source passes through two narrow slits separated by 0.50 mm and produces an interference pattern on a screen 1.5 m away. The wavelength of the light is 600 nm.
(a) Explain why the two slits act as coherent sources. (2 marks)
(b) Calculate the distance between adjacent bright fringes on the screen. (2 marks)
(c) State what would happen to the fringe spacing if the wavelength were halved and explain your answer. (1 mark)
Mark scheme:
(a) Both slits are illuminated by the same laser source, so they emit waves with the same frequency and a constant phase difference – 2 marks
(b)
Use y = Dλ / a
y = (1.5 × 600 × 10⁻⁹) / (0.50 × 10⁻³)
y = 1.8 × 10⁻³ m = 1.8 mm – 2 marks (1 for correct substitution, 1 for correct answer and unit)
(c) Fringe spacing would halve because fringe spacing is directly proportional to wavelength (y ∝ λ) – 1 mark

