OCR Specification focus:
‘Resultant displacement equals vector sum when waves overlap; demonstrate with sound, light, microwaves.’
When two or more waves meet, their displacements combine according to the principle of superposition, forming new patterns that explain interference and other fundamental wave behaviours across physics.
Principle of Superposition
The principle of superposition is one of the most fundamental ideas in wave physics. It describes how multiple waves interact when they overlap in space and time. The behaviour of sound, light, and microwaves — all examples of waves — can be explained through this concept. Superposition underpins phenomena such as interference, standing waves, and resonance, making it essential to the understanding of all oscillatory systems.
Definition and Core Idea
Principle of Superposition: When two or more waves overlap, the resultant displacement at any point is equal to the vector sum of the individual displacements of the overlapping waves.
This means that each wave contributes independently to the total motion of the medium, and the final displacement depends on both the amplitude and phase of each wave at that point.
A schematic of two component waves and their resultant obtained by adding displacements at the same place and time. This directly illustrates the principle of superposition for waves in a linear medium. The colour coding simply distinguishes the contributing waves; no extra physics is implied. Source.
In practical terms, when waves meet:
Their displacements add if they are in phase (crests align with crests, troughs with troughs).
They partially or completely cancel if they are out of phase (crest meets trough).
Understanding Displacement and Vector Addition
The displacement of a wave refers to the distance of a point on the medium from its equilibrium position. Each wave contributes a displacement that may be positive or negative depending on its direction of oscillation. Because displacement is a vector quantity (having both magnitude and direction), the total or resultant displacement is found by vector addition.
For one-dimensional waves on a string, this addition is straightforward: displacements in the same direction add, while those in opposite directions subtract. For waves in two or three dimensions, vector components must be added geometrically.
Conditions for Superposition to Occur
For superposition to apply accurately, the overlapping waves must:
Exist in the same region of space and at the same time.
Originate from coherent sources, meaning they have a constant phase difference and the same frequency.
Travel through a linear medium, where the medium’s response is directly proportional to the applied wave disturbance.
Non-linear media, where large amplitudes distort the response, can violate the principle, leading to complex or unpredictable behaviours.
Mathematical Expression of Superposition
When two waves, each with displacement functions y1y_1y1 and y2y_2y2, overlap at a point, the resultant displacement yyy is given by:
EQUATION
—-----------------------------------------------------------------
Resultant Wave (y) = y₁ + y₂
y₁, y₂ = Individual wave displacements (m)
y = Resultant displacement at a given point (m)
—-----------------------------------------------------------------
If both waves are sinusoidal and have the same frequency, their combined effect can be expressed as:
EQUATION
—-----------------------------------------------------------------
y = A₁sin(ωt) + A₂sin(ωt + φ)
A₁, A₂ = Amplitudes of the waves (m)
ω = Angular frequency (rad s⁻¹)
t = Time (s)
φ = Phase difference (radians)
—-----------------------------------------------------------------
The resulting waveform’s amplitude depends on the relative phase of the two waves.
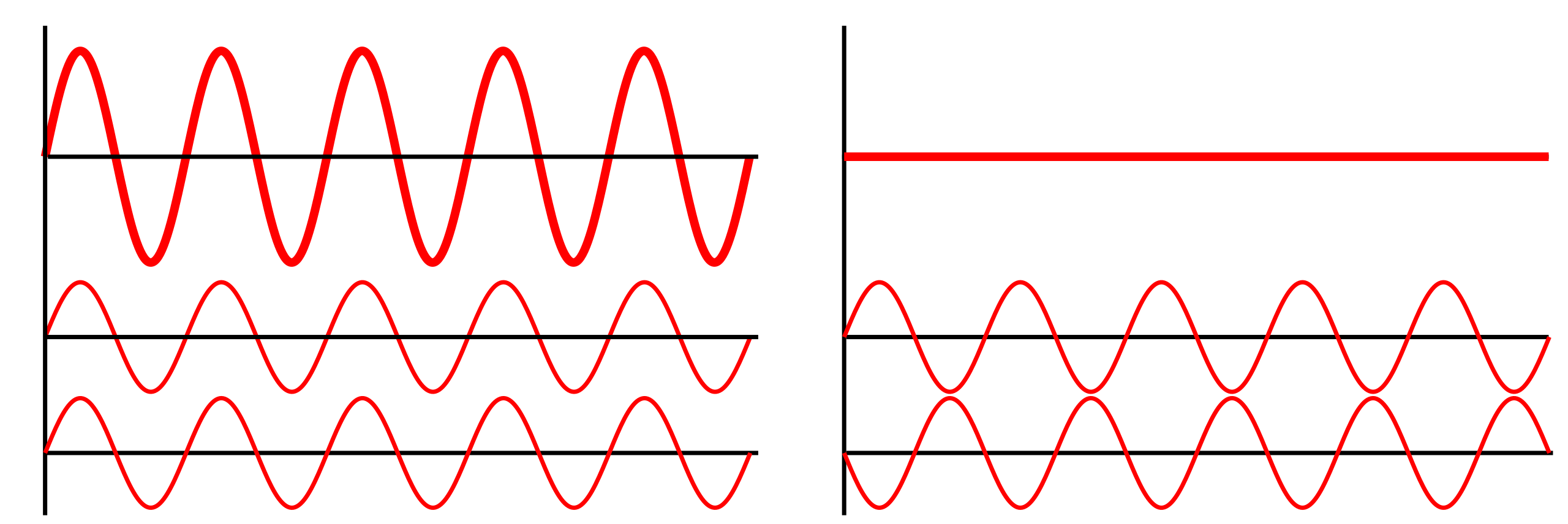
Two equal sine waves add in phase (left) to give a larger-amplitude resultant, and out of phase by 180° (right) to cancel. This is the direct consequence of superposition. Labels are minimal to keep the focus on phase and amplitude. Source.
This relationship underlies both constructive and destructive interference, which are explored further in related subtopics.
Wave Behaviour in Different Contexts
The principle of superposition applies universally to all types of waves — mechanical, electromagnetic, and matter waves. Examples include:
Sound waves in air, leading to beats and interference patterns.
Light waves, producing fringes in interference and diffraction experiments.
Microwave radiation, used to demonstrate interference with easily measurable wavelengths.
In each case, the combined displacement at a point results from the addition of the individual electric, magnetic, or mechanical displacements from each wave.
Constructive and Destructive Outcomes
Although this subsubtopic focuses on the principle itself, it is important to recognise that superposition leads directly to the phenomena of constructive and destructive interference.
Constructive interference occurs when waves meet in phase (φ = 0 or multiples of 2π). Their amplitudes add, creating a wave of greater amplitude.
Destructive interference occurs when waves meet completely out of phase (φ = π, or odd multiples of π). Their amplitudes subtract, reducing or cancelling the resultant displacement.
Real-world patterns often show partial interference, where the resultant amplitude lies between the two extremes.
Vector Nature of Superposition in Two Dimensions
In two-dimensional and three-dimensional wave systems, such as light or water waves, superposition must consider direction. The resultant displacement vector R is the vector sum of all contributing displacement vectors:
EQUATION
—-----------------------------------------------------------------
Resultant Displacement (R) = Σrᵢ
R = Resultant displacement vector
rᵢ = Individual displacement vectors from each wave
—-----------------------------------------------------------------
When visualising this, wavefronts represent points of equal phase. Where wavefronts intersect, the amplitudes combine to form regions of maximum or minimum displacement — visible as bright and dark fringes in light interference experiments.
Superposition in Sound, Light, and Microwaves
OCR emphasises the demonstration of superposition using sound, light, and microwaves. These examples reinforce that the principle operates consistently across different types of waves.
Sound: When two speakers emit the same tone, alternating loud and quiet regions form due to constructive and destructive interference.
Light: The classical Young’s double-slit experiment demonstrates that overlapping light waves form bright and dark fringes.
Microwaves: Microwave sources and detectors in a lab setup reveal variations in intensity as a detector moves through regions of constructive and destructive interference.
Each of these cases illustrates that the principle of superposition governs the spatial variation in amplitude, which can be measured as intensity in practical observations.
Importance in Wave Physics
The principle of superposition provides the mathematical and conceptual basis for:
Interference and diffraction patterns.
Formation of stationary waves, where reflected and incident waves combine.
Resonance phenomena, where particular frequencies reinforce displacement amplitudes.
Analysis of complex waveforms, by decomposing them into simpler sinusoidal components through Fourier methods.
Without the superposition principle, these wave behaviours could not be predicted or described quantitatively. It remains one of the central ideas linking diverse wave phenomena across all areas of physics, from acoustics to quantum mechanics.
FAQ
The principle of superposition still applies, regardless of how many waves are involved. Each wave contributes independently to the total displacement.
To find the resultant displacement:
Add the displacements from all waves vectorially at that instant.
If several waves are in phase, their amplitudes add constructively.
If their phases differ, the resultant depends on the relative phase relationships.
This principle is essential for understanding complex waveforms such as those in musical sounds or interference from multiple light sources.
Yes, it applies to all waves in a linear medium. Even if a wave is not sinusoidal, it can be considered as a combination of many sine waves through Fourier analysis.
Each sine component obeys the principle of superposition independently. When these are summed, they recreate the complex waveform.
This is how sound synthesis, signal analysis, and many areas of modern physics use superposition to study real-world waveforms.
In non-linear media, the response of the medium is not directly proportional to the applied disturbance. As a result, waves interact and distort each other instead of adding linearly.
Common examples include:
Large amplitude water waves that break or form turbulence.
High-intensity sound where pressure variations are too large for linear assumptions.
Powerful laser light in certain crystals, where frequencies combine to produce new light (e.g., second-harmonic generation).
In such cases, superposition no longer gives accurate results.
The phase difference determines how the peaks and troughs of waves align.
In phase (0 radians): Crests and troughs coincide, giving maximum amplitude (constructive interference).
Out of phase (π radians): Crests meet troughs, cancelling displacement (destructive interference).
Intermediate phases: Produce partial reinforcement or cancellation depending on the degree of phase difference.
Thus, phase directly controls the degree of interference and the observed intensity of the resultant wave.
Yes, but in a different context. In quantum mechanics, wavefunctions describing particles can also superpose.
When two or more quantum states overlap, their wavefunctions add, and probabilities depend on the square of the resultant amplitude.
This leads to quantum interference, seen in experiments like the electron double-slit. While mathematically similar, the interpretation involves probabilities rather than physical displacements, making it a conceptual extension of classical superposition.
Practice Questions
Question 1 (2 marks)
Two progressive waves of the same frequency and amplitude meet at a point in phase.
(a) State what is meant by the principle of superposition.
(b) Describe the resultant displacement at that point.
Mark scheme:
(a) 1 mark – The resultant displacement at any point is the vector sum of the displacements of the individual waves.
(b) 1 mark – The waves add constructively, producing a resultant with twice the amplitude of either individual wave.
Question 2 (5 marks)
Two sound waves, each of frequency 500 Hz and equal amplitude, overlap in air.
At one point in space the waves arrive in phase, while at another point they arrive completely out of phase.
(a) Explain, using the principle of superposition, what happens at each of these points. (3 marks)
(b) State the condition for complete destructive interference in terms of phase difference and path difference. (2 marks)
Mark scheme:
(a)
1 mark – When the waves arrive in phase, their displacements add constructively.
1 mark – The resultant amplitude is the sum of the two individual amplitudes.
1 mark – When the waves arrive out of phase (crest meets trough), the displacements cancel, giving zero resultant displacement.
(b)
1 mark – For complete destructive interference, the phase difference is 180° (π radians).
1 mark – The path difference is (n + ½)λ, where n is any integer.

