OCR Specification focus:
‘Einstein’s equation: hf = Φ + KE_max, with Φ the work function; define threshold frequency.’
Einstein’s photoelectric equation describes how individual photons interact with electrons in a metal, explaining photoelectric emission through quantised energy transfer and establishing key relationships between frequency, work function, and kinetic energy.
The Photoelectric Effect and Photon Energy Transfer
The photoelectric effect is the emission of electrons from a metal surface when light of sufficient frequency shines upon it. Classical wave theory could not explain the observed behaviour of this phenomenon — particularly why electrons are emitted only above a certain threshold frequency and why their maximum kinetic energy depends solely on light frequency, not intensity. These inconsistencies led Albert Einstein in 1905 to propose a new quantum model of light, introducing the concept that light consists of discrete packets of energy called photons.
Each photon has an energy proportional to its frequency. When a photon collides with an electron in a metal surface, it transfers its energy in a one-to-one interaction. If this energy exceeds the work function of the material, the electron can escape from the surface.
Photon–Electron Interaction and Energy Conservation
Einstein’s theory assumes energy conservation applies at the microscopic level of individual photon–electron interactions. The total energy of a photon is distributed between overcoming the metal’s work function (the minimum energy required to release an electron) and the kinetic energy of the emitted photoelectron. This energy balance forms the basis of Einstein’s photoelectric equation.
EQUATION
—-----------------------------------------------------------------
Einstein’s Photoelectric Equation
hf = Φ + KE_max
h = Planck’s constant (6.63 × 10⁻³⁴ J·s)
f = frequency of incident radiation (Hz)
Φ = work function of the metal (J)
KE_max = maximum kinetic energy of emitted photoelectron (J)
—-----------------------------------------------------------------
In this equation, hf represents the photon’s energy. The work function corresponds to the binding energy that must be overcome for an electron to escape the surface, while KE_max refers to the greatest kinetic energy among all emitted electrons.
The Concept of Threshold Frequency
If the frequency of incident radiation is below a certain threshold frequency (f₀), no electrons are emitted regardless of light intensity. This is because the photon energy is insufficient to overcome the metal’s work function.
Threshold Frequency: The minimum frequency of electromagnetic radiation required to just release electrons from a metal surface.
At the threshold condition, emitted electrons have zero kinetic energy, meaning the photon’s energy exactly equals the work function: hf₀ = Φ. Therefore, Einstein’s photoelectric equation can also be expressed as KE_max = h(f – f₀), revealing a direct linear relationship between the maximum kinetic energy of photoelectrons and the frequency of incident radiation.
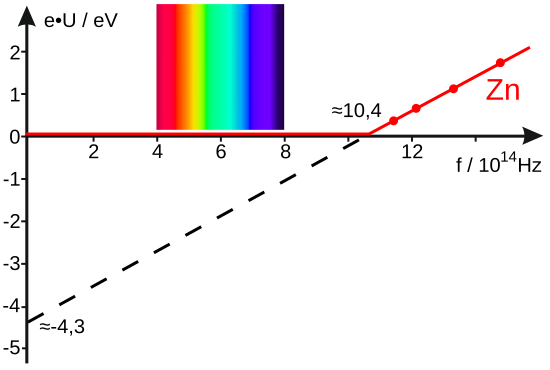
Plot of maximum kinetic energy against frequency for two different metals, each line having the same slope h but different intercepts reflecting distinct work functions and threshold frequencies. This directly illustrates K_max = h(f - f₀). The diagram is minimal and clearly labelled, with no extraneous information. Source.
Experimental Verification and Graphical Interpretation
Einstein’s photoelectric equation can be experimentally tested by measuring the stopping potential in a vacuum photocell apparatus.
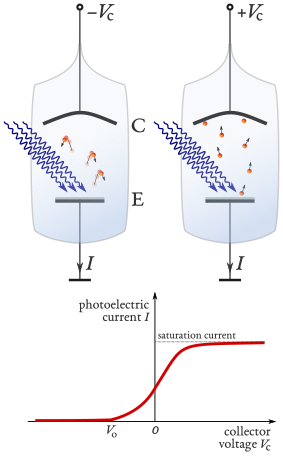
Schematic of a photoelectric-effect apparatus showing an evacuated tube with an emitter (E) and collector (C), illuminated by monochromatic light. The applied potential can be reversed to determine the stopping potential that just prevents the most energetic photoelectrons from reaching the collector. Extra detail shown includes the ammeter and voltmeter used to record photocurrent and potential difference (appropriate and helpful for OCR level). Source.
The stopping potential (V_s) is the minimum potential difference needed to prevent the most energetic photoelectrons from reaching the anode. The relationship between maximum kinetic energy and stopping potential is given by:
EQUATION
—-----------------------------------------------------------------
Photoelectron Energy Relation
KE_max = eV_s
e = elementary charge (1.60 × 10⁻¹⁹ C)
V_s = stopping potential (V)
—-----------------------------------------------------------------
Combining this with Einstein’s equation gives eV_s = hf – Φ. A graph of V_s against f produces a straight line with gradient h/e and a frequency-axis intercept at f₀.
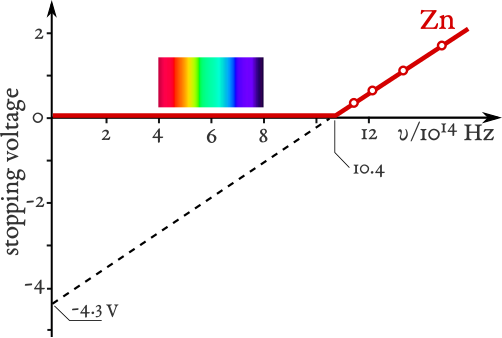
Stopping potential (V_s) versus frequency (f) for zinc, showing a straight line with slope h/e and an intercept at the threshold frequency f₀. This directly visualises the rearranged form eV_s = hf - Φ. The plot is clean and annotated for quick extraction of h and Φ. Source.
This provides an experimental method to determine Planck’s constant and to confirm the validity of the photon model.
The linear relationship observed in such experiments offered one of the earliest and most convincing demonstrations that light energy is quantised. Classical wave theory could not account for this proportionality, as it predicted a dependence on light intensity rather than frequency.
The Role of the Work Function and Metal Dependence
The work function varies between materials and is influenced by their surface conditions. Metals with low work functions, such as caesium and sodium, emit electrons under visible light, whereas others like copper or zinc require ultraviolet radiation.
Work Function (Φ): The minimum energy needed to remove an electron from the surface of a metal to a point just outside the metal, where it has zero kinetic energy.
A smaller work function implies a lower threshold frequency, making emission easier to achieve with lower-frequency photons. The value of Φ is an intrinsic property of each material and is often expressed in electronvolts (eV) for convenience in quantum and atomic physics contexts.
Implications for Quantum Theory
Einstein’s explanation of the photoelectric effect confirmed that electromagnetic radiation behaves as a stream of quantised energy packets, establishing a cornerstone of quantum theory. This quantisation resolved the contradictions of classical physics, which treated light purely as a wave. The success of the photoelectric equation also reinforced the concept of wave–particle duality, later extended to matter by Louis de Broglie.
By proposing that photons possess both wave and particle characteristics, Einstein’s work unified energy conservation principles with discrete energy transfer mechanisms. The equation not only explained observed photoelectric behaviour but also paved the way for the development of quantum mechanics, reshaping the understanding of atomic and subatomic processes.
Summary of Key Relationships and Conceptual Links
Photon energy is proportional to frequency: E = hf.
Emission occurs only if hf ≥ Φ.
Threshold frequency marks the energy boundary where photoemission begins.
Maximum kinetic energy depends linearly on frequency, not on light intensity.
Stopping potential measurements provide experimental determination of Planck’s constant.
Work function values vary between metals, determining their sensitivity to light of different wavelengths.
These relationships encapsulate Einstein’s central insight: energy exchange between light and matter occurs in quantised units, and only photons with sufficient energy can liberate electrons from metal surfaces. His equation elegantly captures the balance between energy input and energy expenditure during photoemission, a defining moment in the evolution of modern physics.
FAQ
The stopping potential is the voltage required to reduce the photocurrent to zero in a photoelectric experiment. It provides a direct measure of the maximum kinetic energy of emitted electrons.
When an opposing potential equal to the stopping potential is applied, even the most energetic photoelectrons cannot reach the anode.
The relationship is given by:
KE_max = eV_s, where e is the elementary charge.
Thus, measuring V_s allows experimental determination of KE_max and, when repeated for various light frequencies, helps verify Einstein’s photoelectric equation.
Electrons in a metal occupy a range of energy levels up to the Fermi level.
Electrons deeper within the metal require additional energy to reach the surface before escaping.
Those nearer the surface need less energy to overcome the work function.
Consequently, even when all photons have the same energy (hf), the emitted electrons display a distribution of kinetic energies up to a maximum value, KE_max = hf – Φ.
The work function depends on both the intrinsic material properties and surface conditions.
Surface contamination or oxidation can increase the effective work function by forming a thin insulating layer.
Temperature changes can slightly alter electron energy distributions.
Surface roughness or crystal orientation affects how tightly electrons are bound.
Careful cleaning and maintaining the metal under vacuum conditions ensure accurate and reproducible measurements of Φ in photoelectric experiments.
For light frequencies above the threshold frequency:
Increasing intensity increases the number of photons incident per second.
Since each photon can liberate at most one electron, the rate of electron emission (photoelectric current) increases proportionally.
However, the energy per electron (KE_max) remains unchanged because it depends only on the photon frequency, not the number of photons.
This distinction between current and kinetic energy was key evidence for the photon model of light.
Einstein’s interpretation demonstrated that electromagnetic radiation behaves as a stream of discrete energy quanta, not continuous waves.
His theory explained phenomena that classical physics could not, such as:
Instantaneous emission of photoelectrons despite low light intensity.
The existence of a threshold frequency.
Linear dependence of KE_max on frequency.
This work provided direct evidence for energy quantisation and established photons as real physical entities, forming a foundation for the development of modern quantum mechanics.
Practice Questions
Question 1 (2 marks)
A metal surface has a work function of 3.0 × 10⁻¹⁹ J. Calculate the threshold frequency for the photoelectric emission of electrons from this surface.
(You may use Planck’s constant h = 6.63 × 10⁻³⁴ J·s.)
Mark Scheme for Question 1
Correct use of the photoelectric threshold equation hf₀ = Φ (1 mark)
Correct substitution and calculation of f₀ = Φ / h = (3.0 × 10⁻¹⁹) / (6.63 × 10⁻³⁴) = 4.52 × 10¹⁴ Hz (1 mark)
Question 2 (5 marks)
Explain how Einstein’s photoelectric equation accounts for both the existence of a threshold frequency and the independence of maximum photoelectron kinetic energy from light intensity. In your answer, refer to the energy of individual photons and the work function of the metal.
Mark Scheme for Question 2
States that each photon transfers its energy to a single electron in a one-to-one interaction (1 mark)
States that photon energy is given by E = hf (1 mark)
Explains that electrons are only emitted when hf ≥ Φ, as energy must be sufficient to overcome the work function (1 mark)
Explains that threshold frequency (f₀) corresponds to hf₀ = Φ; below this no emission occurs regardless of intensity (1 mark)
Explains that maximum kinetic energy (KE_max = hf – Φ) depends only on the photon frequency, so increasing intensity increases the number of photons but not their energy, hence KE_max is unchanged (1 mark)

