The photoelectric effect demonstrates how light can eject electrons from a metal surface, providing crucial evidence for the particle nature of light. This subtopic explores how varying light intensity affects the maximum kinetic energy of emitted photoelectrons, revealing the fundamental role of photon energy rather than wave amplitude.

Understanding the Photoelectric Effect

When electromagnetic radiation of sufficiently high frequency strikes a metal surface, electrons are emitted. These electrons are called photoelectrons. The phenomenon cannot be explained by classical wave theory, which predicted that light intensity alone should determine the energy of emitted electrons. Instead, experimental evidence shows that light frequency, not intensity, governs whether emission occurs and the energy of the ejected electrons.

Each electron in the metal can only absorb energy from a single photon — a discrete packet of electromagnetic energy. The amount of energy carried by each photon depends solely on the radiation frequency.

EQUATION
—-----------------------------------------------------------------
Photon Energy (E) = h f
E = Energy of a photon (joules, J)
h = Planck’s constant (6.63 × 10⁻³⁴ J s)
f = Frequency of the incident radiation (hertz, Hz)
—-----------------------------------------------------------------

Thus, for photoelectric emission to occur, the photon energy must exceed the work function of the metal — the minimum energy required to release an electron from the surface.

The Threshold Frequency

Every metal has a characteristic threshold frequency. Below this frequency, no electrons are emitted, regardless of the intensity of the light. This demonstrates that the photoelectric effect is a quantum process dependent on photon energy, not cumulative wave energy.

If the frequency is above the threshold, emission occurs immediately, and the excess photon energy appears as kinetic energy of the emitted electron.

Einstein’s Photoelectric Equation

Einstein proposed an energy conservation relationship for the photoelectric effect that links photon energy, the work function, and the kinetic energy of the emitted electron.

EQUATION
—-----------------------------------------------------------------
Einstein’s Photoelectric Equation: h f = Φ + Kₑ(max)
h f = Energy of incident photon (J)
Φ = Work function of the metal (J)
Kₑ(max) = Maximum kinetic energy of emitted electron (J)
—-----------------------------------------------------------------

This equation shows that the maximum kinetic energy of photoelectrons depends only on the frequency of the incident radiation and the material’s work function — not the intensity.

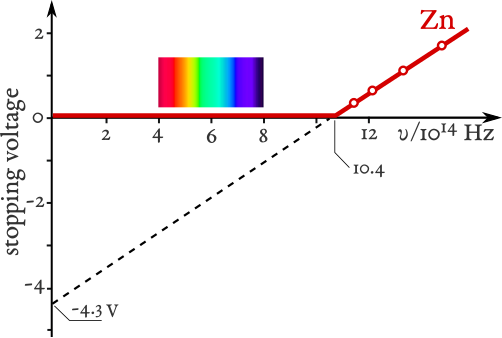
Stopping potential VsV_sVs​ (proportional to KmaxK_\text{max}Kmax​) plotted against frequency for zinc. The linear relation and x-intercept mark the threshold frequency. The labelled metal (Zn) is specific, but the relationship holds for any photoemissive material. Source.

Intensity of Radiation and Its Meaning

In the context of the photoelectric effect, intensity refers to the total energy incident on the metal surface per unit area per second. Increasing intensity means increasing the number of photons striking the surface each second, but each photon retains the same energy determined by its frequency.

Therefore, intensity influences the rate at which electrons are emitted but not their individual energies.

Independence of Maximum Kinetic Energy from Intensity

Experimental evidence shows that once the threshold frequency is exceeded, increasing the light intensity increases the number of photoelectrons emitted but not their maximum kinetic energy. Each photoelectron receives energy from a single photon; since photon energy depends only on frequency, not on intensity, the kinetic energy remains constant for a given frequency.

Key points:

• Photon energy (h f) determines whether emission occurs and the maximum kinetic energy of emitted electrons.

• Light intensity affects how many photons strike the surface per second, influencing the emission rate, not the electron energy.

• If intensity increases while frequency remains constant (and above threshold), more electrons are emitted per second, but each has the same maximum kinetic energy.

• Below the threshold frequency, no electrons are emitted, regardless of how high the intensity is.

This behaviour is consistent with the particle model of light but not with classical wave predictions, which would expect the energy of emitted electrons to increase with light amplitude (intensity).

Experimental Observations

Typical photoelectric experiments involve shining monochromatic light of varying intensity on a metal surface and measuring the stopping potential — the potential difference needed to stop the fastest electrons from reaching the detector. The stopping potential provides a direct measure of the maximum kinetic energy of emitted electrons.

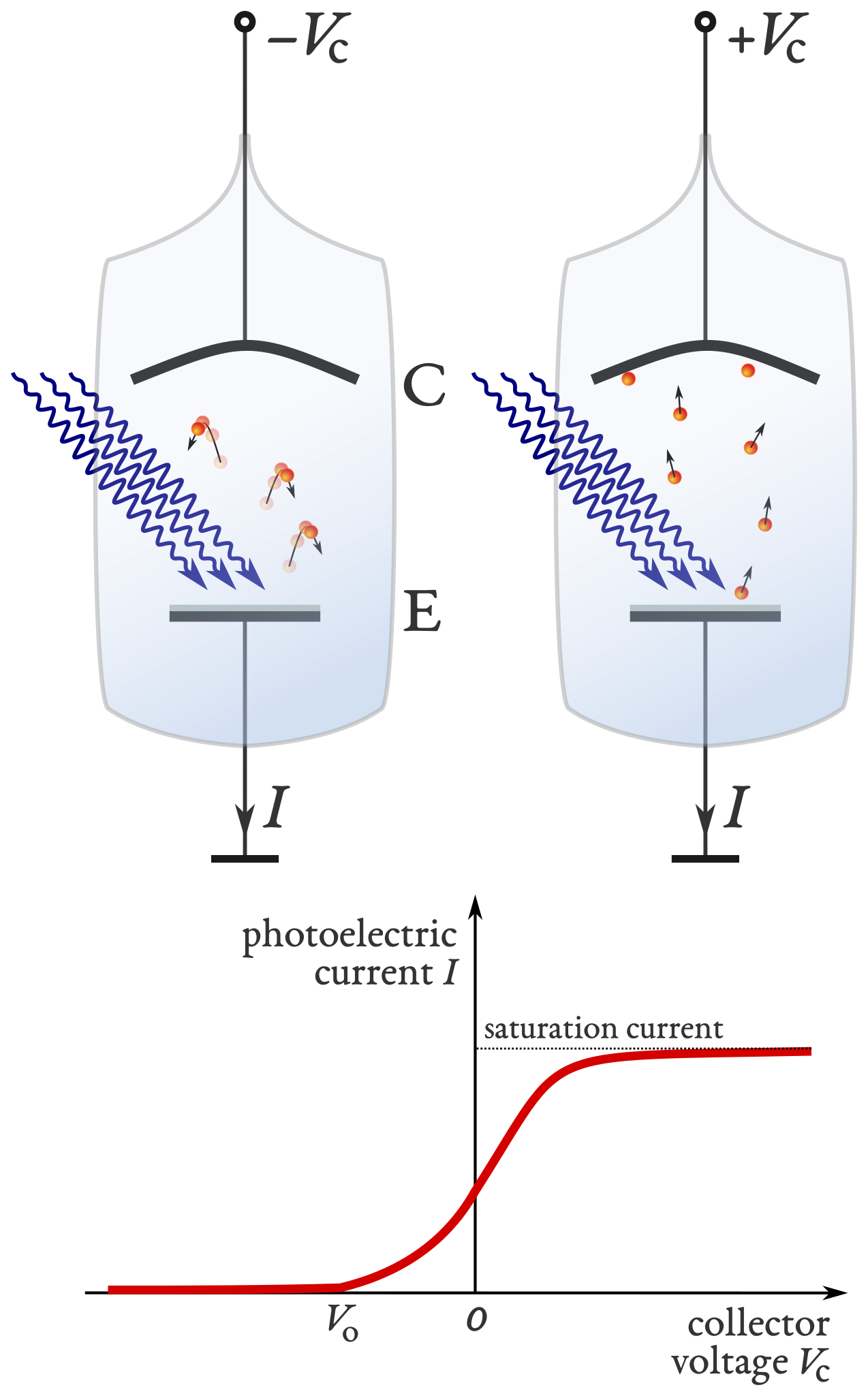
Schematic of a photoelectric tube showing emitter (E), collector (C), and applied potential used to determine the stopping potential. Extra detail: the caption also mentions saturation current (related to high intensity), which goes beyond the OCR requirement but does not add conceptual complexity. Source.

EQUATION
—-----------------------------------------------------------------
Kₑ(max) = e Vₛ
Kₑ(max) = Maximum kinetic energy of emitted electron (J)
e = Elementary charge (1.60 × 10⁻¹⁹ C)
Vₛ = Stopping potential (V)
—-----------------------------------------------------------------

Observations reveal that:

• For a given frequency (above threshold), increasing intensity increases current (more photoelectrons) but leaves the stopping potential unchanged.

• For higher frequencies, the stopping potential — and hence the maximum kinetic energy — increases, confirming dependence on photon energy.

Conceptual Explanation

The independence of maximum kinetic energy from intensity can be reasoned through one-to-one photon–electron interactions. Each photon interacts with only one electron, transferring its discrete energy quantum. Therefore:

• The energy per photon remains constant for a given frequency.

• Increasing intensity simply means more photons, so more interactions occur, resulting in higher emission rates but not greater individual energies.

• The frequency of the photons sets the energy ceiling for emitted electrons, explaining why maximum kinetic energy remains fixed as intensity changes.

This direct proportionality between photon energy and electron kinetic energy was a pivotal piece of evidence leading to the acceptance of quantum theory in physics. It showed that electromagnetic radiation behaves as if composed of discrete particles — photons — contradicting classical wave models.

Summary of Key Relationships

• Photon energy E = h f.

• Photoemission requires h f ≥ Φ.

• Kₑ(max) = h f – Φ.

• Intensity ↑ ⇒ Emission rate ↑ but Kₑ(max) unchanged.

These principles underpin our understanding of the quantum behaviour of light and matter, defining a cornerstone of modern physics.