OCR Specification focus:
‘Discuss limits of wave behaviour for macroscopic objects due to extremely small λ.’
The concept of wave–particle duality extends to all matter, but its effects are only observable at very small scales. Understanding why wave behaviour becomes undetectable in macroscopic objects reveals key insights into the practical limits of quantum mechanics.
Wave–Particle Duality and Its Universal Application
The wave–particle duality principle proposes that all particles exhibit both wave-like and particle-like characteristics. While light displays interference and diffraction, the same principle applies to matter, including electrons, atoms, and larger particles.
Wave–Particle Duality: The concept that all matter and electromagnetic radiation exhibit both wave and particle properties, depending on how they are observed.
In quantum theory, this idea is quantified by the de Broglie wavelength, which links a particle’s momentum to a wavelength that represents its wave-like nature.
EQUATION
—-----------------------------------------------------------------
de Broglie Wavelength (λ) = h / p
λ = Wavelength (metre, m)
h = Planck’s constant (6.63 × 10⁻³⁴ J s)
p = Momentum of the particle (kg m s⁻¹)
—-----------------------------------------------------------------
This fundamental relationship applies to all objects — from subatomic particles to humans — though its effects are perceptible only when the wavelength is comparable to the scale of the object or its environment.
Why Macroscopic Objects Do Not Exhibit Observable Wave Behaviour
The magnitude of Planck’s constant (h) is extremely small. As a result, when applied to macroscopic masses moving at everyday speeds, the de Broglie wavelength becomes negligibly tiny. This explains why a football, car, or person does not produce observable interference or diffraction patterns.
Calculation Perspective
For a typical electron moving at 1 × 10⁶ m/s, λ is around 10⁻¹⁰ m — comparable to atomic spacing, making diffraction measurable. However, for a 0.1 kg object moving at 1 m/s, λ is approximately 10⁻³³ m, far smaller than any detectable distance.

Historic electron diffraction photograph from G. P. Thomson’s laboratory showing ring patterns from a polycrystalline target. The rings evidence electron wave-like behaviour when λ matches atomic lattice spacings. The archival nature adds historical context beyond OCR requirements but directly supports the scale argument. Source.
The wavelength is therefore too small to cause measurable interference, so wave properties disappear at macroscopic scales.
The Transition from Quantum to Classical Domains
Physics distinguishes between quantum behaviour (dominant for very small particles) and classical behaviour (applicable to large-scale objects). This transition does not represent a sudden change in laws, but rather a gradual loss of observable quantum effects as systems increase in size and energy.
Factors Limiting Observable Duality
Mass of the Object – As mass increases, momentum (p = mv) becomes very large, reducing the de Broglie wavelength dramatically.
Velocity – Even at high speeds, a large mass gives an insignificantly small wavelength.
Environmental Interaction – Larger objects interact continuously with surrounding particles, causing rapid decoherence, which suppresses quantum effects.
Measurement Precision – The wavelength of macroscopic objects lies far beyond the resolution of any experimental apparatus.
These factors ensure that wave–particle duality remains confined to microscopic entities such as electrons, atoms, and molecules.
The Concept of Decoherence
In quantum mechanics, decoherence explains how superposition states collapse into definite outcomes through environmental interaction.
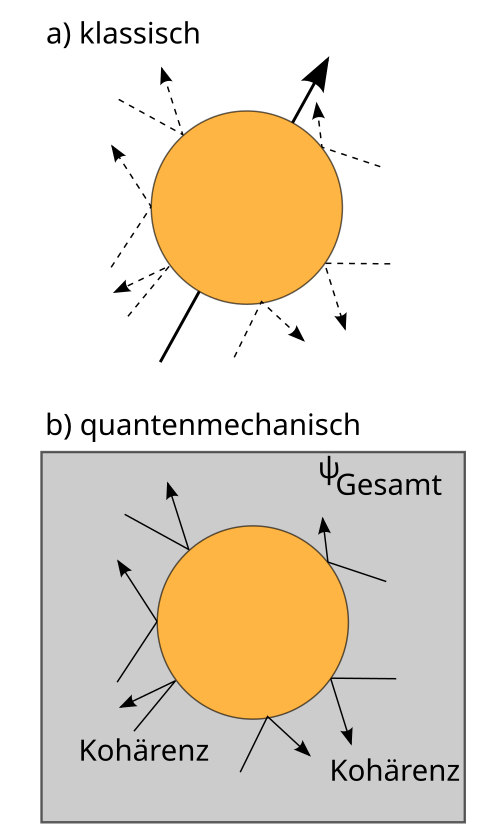
Schematic illustration of quantum decoherence, contrasting coherent superposition with classical, effectively stochastic behaviour after environmental coupling. It highlights how interactions with many degrees of freedom destroy phase relations, suppressing interference in macroscopic systems. The level of detail slightly exceeds OCR requirements by naming ‘classical collision’ for contrast, but remains directly supportive of the syllabus focus on limits of wave behaviour. Source.
Decoherence: The process by which quantum systems lose their coherent superpositions due to interactions with their environment, leading to classical behaviour.
Even though the underlying laws of quantum mechanics apply universally, decoherence effectively prevents macroscopic objects from displaying interference or diffraction. This marks the boundary between the quantum realm, where probabilities dominate, and the classical realm, where deterministic physics prevails.
Scale and the Limits of Quantum Effects
The ability to observe quantum wave phenomena depends on comparing the de Broglie wavelength to physical dimensions in an experiment.
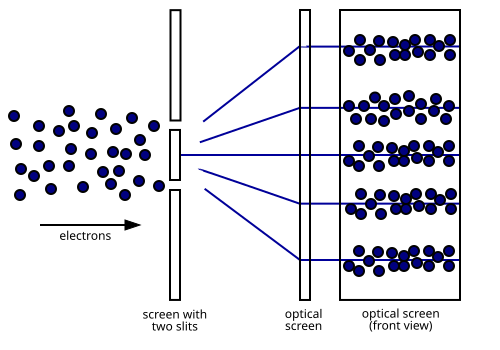
Diagram of the electron double-slit experiment showing interference fringes produced by single-particle matter waves. Interference appears because the de Broglie wavelength is comparable to slit spacing and screen scale. This directly visualises wave behaviour that becomes unobservable for macroscopic objects with extremely small λ. Source.
For diffraction or interference to occur, the wavelength must be comparable to the feature size of the obstacle or slit.
When dealing with macroscopic scales, even in nanostructured materials, the corresponding wavelengths are many orders of magnitude smaller. Therefore, no observable diffraction or interference patterns emerge for large objects.
Comparative Scale Examples
Electron diffraction occurs with wavelengths similar to atomic spacing (~10⁻¹⁰ m).
Neutron diffraction, though rarer, works due to slightly longer wavelengths (~10⁻¹⁴ m).
Molecules such as C₆₀ (buckminsterfullerene) have been shown to exhibit interference, but only under highly controlled laboratory conditions.
Everyday macroscopic objects (e.g., grains of dust) have wavelengths vastly smaller than subatomic distances (~10⁻³⁰ m or less), making any wave effects completely unobservable.
Implications for the Nature of Reality
Despite the absence of observable wave behaviour in macroscopic systems, wave–particle duality remains a cornerstone of quantum physics. It implies that all matter, regardless of scale, fundamentally follows quantum principles, even if those effects are hidden by environmental and scale-related constraints.
This understanding bridges the microscopic quantum world and the macroscopic classical world, showing that classical mechanics is simply a limiting case of quantum theory, where the de Broglie wavelength becomes vanishingly small.
Summary of Key Ideas Across Scales
All matter exhibits wave–particle duality, but detectability depends on wavelength size relative to object scale.
de Broglie wavelength provides a quantitative measure linking mass and velocity to wave behaviour.
Macroscopic objects possess wavelengths far too small to produce observable interference or diffraction.
Decoherence explains the apparent disappearance of quantum effects in large systems.
Quantum mechanics remains universally valid; classical physics emerges naturally as a large-scale approximation.
FAQ
Quantum effects such as diffraction or interference become undetectable when the de Broglie wavelength is vastly smaller than the physical scale of the system.
For macroscopic objects, this typically means wavelengths below 10⁻²⁰ m, far beyond experimental reach.
At such scales, no known measurement device or experimental geometry can resolve the interference fringes, and environmental noise completely masks any remaining coherence.
Large molecules can exhibit interference patterns when isolated from environmental interactions.
The molecules must travel slowly in a high vacuum to maintain coherence.
Experimental slits or gratings must have dimensions comparable to their de Broglie wavelength (~10⁻¹² to 10⁻¹³ m).
Cooling the molecules reduces internal motion, limiting decoherence.
This demonstrates that wave–particle duality persists for large systems but becomes increasingly fragile as complexity grows.
Yes. Higher temperatures increase particle energy and motion, which enhances environmental interactions and accelerates decoherence.
In contrast, near absolute zero, thermal vibrations and collisions are reduced, allowing quantum coherence to persist longer.
This is why experiments showing macroscopic quantum states—such as superconductivity or superfluidity—occur only at extremely low temperatures.
Only under highly controlled laboratory conditions where decoherence is minimised.
Examples include:
Superconductors, where electron pairs behave coherently across a macroscopic distance.
Bose–Einstein condensates, in which thousands of atoms occupy the same quantum state.
Although these systems show collective quantum behaviour, individual objects within them still obey classical physics when isolated from their quantum environment.
Measurement interacts with a system and effectively forces it into one of several possible outcomes, breaking superposition.
Every observation involves energy transfer and coupling to the environment, which destroys phase relationships between quantum states.
This process links to the measurement problem in quantum mechanics and is a practical reason why macroscopic objects appear to behave classically — their quantum states are constantly being “measured” by their surroundings.
Practice Questions
Question 1 (2 marks)
Explain why the wave-like behaviour of macroscopic objects, such as a football, cannot be observed in everyday situations.
Mark scheme:
1 mark for stating that the de Broglie wavelength of macroscopic objects is extremely small due to their large mass.
1 mark for explaining that this wavelength is far smaller than any measurable or observable scale, so no interference or diffraction can occur.
Question 2 (5 marks)
The de Broglie wavelength of a particle is given by λ = h / p. Discuss how this relationship explains the limits of observable wave–particle duality across different scales, from electrons to everyday macroscopic objects. In your answer, refer to how mass and velocity affect wavelength and describe why wave effects are not seen for large objects.
Mark scheme:
1 mark for correctly identifying that λ = h / p links wavelength to momentum.
1 mark for recognising that increasing mass or velocity increases momentum, reducing the wavelength.
1 mark for explaining that only when λ is comparable to the size of experimental features (such as slit spacing or atomic separations) can diffraction or interference occur.
1 mark for stating that for macroscopic objects, the wavelength is many orders of magnitude smaller than any detectable dimension.
1 mark for concluding that this makes wave–particle duality unobservable at large scales, so classical behaviour dominates.

