OCR Specification focus:
‘Define geostationary orbit and discuss telecommunications uses and prediction with Newtonian laws.’
Geostationary Orbits and Their Uses
A geostationary orbit is a special circular orbit in which a satellite remains fixed above one point on Earth’s equator, enabling continuous communication links vital for modern applications.
Understanding Geostationary Orbits
A geostationary orbit is a specific case of a geosynchronous orbit, meaning its orbital period matches Earth’s rotation period.
A diagram showing a geosynchronous satellite positioned above a fixed point on the equator, where its orbital motion matches Earth’s rotation. Source.
To appreciate why this orbit is so significant, it is essential to recognise what conditions must be satisfied for a satellite to appear motionless relative to the Earth’s surface.
Geostationary orbit: An orbit in which a satellite remains above the same point on Earth’s equator by completing one orbit in the same time that Earth rotates.
A satellite in a geostationary orbit matches Earth’s sidereal rotational period, which is approximately 23 hours 56 minutes. Because the satellite travels in the same direction as Earth’s rotation, and with identical angular velocity, it appears fixed above a single longitude when viewed from the ground. This property makes it especially valuable for continuous data transmission.
Conditions Required for a Geostationary Orbit
To maintain a geostationary position, the satellite must satisfy strict physical constraints based on Newtonian gravitation and uniform circular motion. These constraints explain why such an orbit cannot be placed at arbitrary radii or inclinations. Instead, only one unique orbital radius allows the orbital period to match Earth’s rotation.
EQUATION
—-----------------------------------------------------------------
Orbital Period–Radius Relation (T²–r³) = T² = (4π²/GM) r³
T = Orbital period of the satellite (s)
G = Gravitational constant (N m² kg⁻²)
M = Mass of Earth (kg)
r = Orbital radius from Earth’s centre (m)
—-----------------------------------------------------------------
Using this relationship, we find that geostationary satellites occupy a circular orbit at approximately 36,000 km above Earth’s surface.
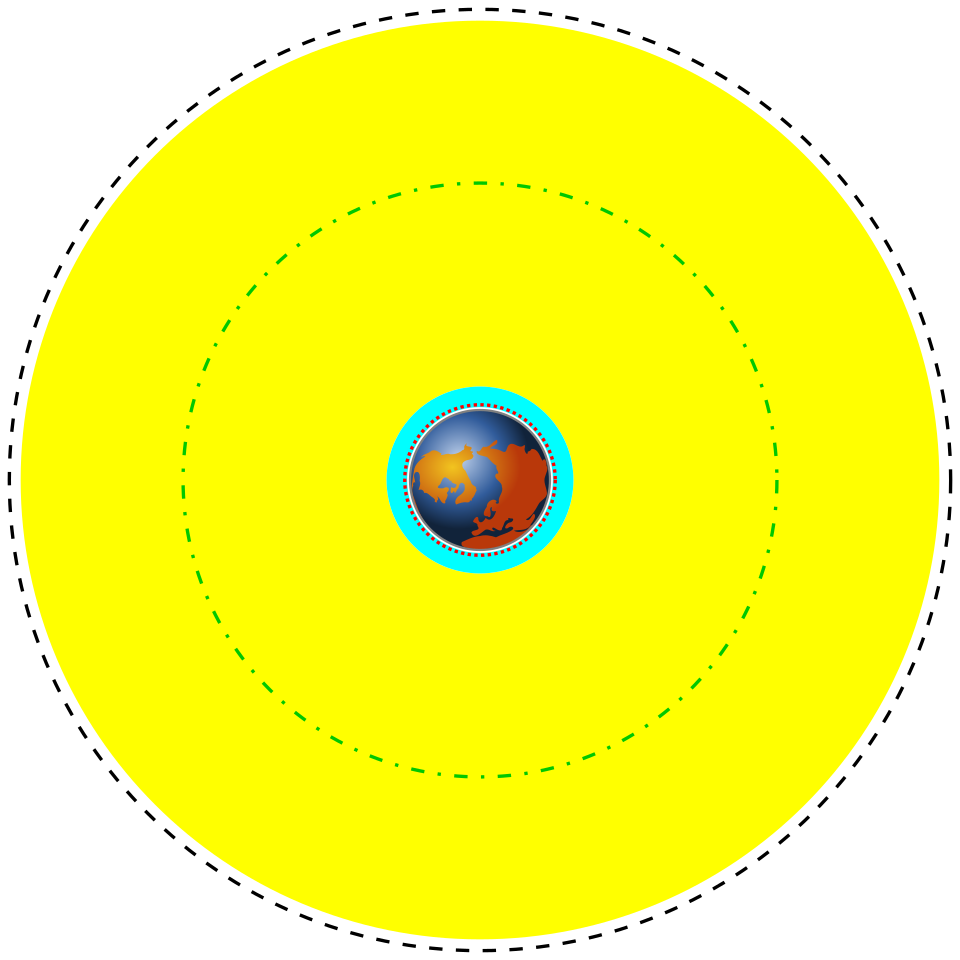
A scale diagram of Earth and surrounding orbital regions, with the geostationary orbit highlighted far beyond LEO and MEO, consistent with the large radius required for a 24-hour period. Source.
Importantly, the satellite must orbit in the equatorial plane, since only this orientation ensures that the satellite does not drift north or south relative to the observer.
Why Gravity Provides the Required Centripetal Force
The satellite is held in orbit because Earth’s gravitational force acts as the centripetal force, keeping it moving in a circular path. Because the gravitational force decreases with distance according to Newton’s inverse-square law, only at one specific radius is the balance between gravitational force and the satellite’s required centripetal acceleration satisfied. This demonstrates that geostationary orbits can be accurately predicted using Newton’s laws of motion and Newton’s law of gravitation.
Once in orbit, satellites still require occasional adjustments using small onboard thrusters to counteract perturbations from gravitational influences of the Moon and Sun, pressure from solar radiation, and irregularities in Earth’s gravitational field. However, these adjustments are minor compared to the dominant gravitational force keeping the satellite in orbit.
Structure and Features of a Geostationary Satellite System
Geostationary satellites form the backbone of many communication networks. Their constant position allows ground-based antennae to remain stationary, simplifying installation and maintenance. Key features of geostationary systems include:
Fixed ground receivers that do not require tracking mechanisms.
Large coverage areas, typically spanning around one-third of Earth’s surface per satellite.
Continuous line-of-sight between satellite and ground station, essential for high-reliability communication links.
High altitude, reducing atmospheric interference and enabling stable long-distance signal propagation.
Because three satellites spaced evenly around the equator can cover almost the entire globe (excluding high-latitude regions), global communication systems often rely on networks of geostationary satellites.
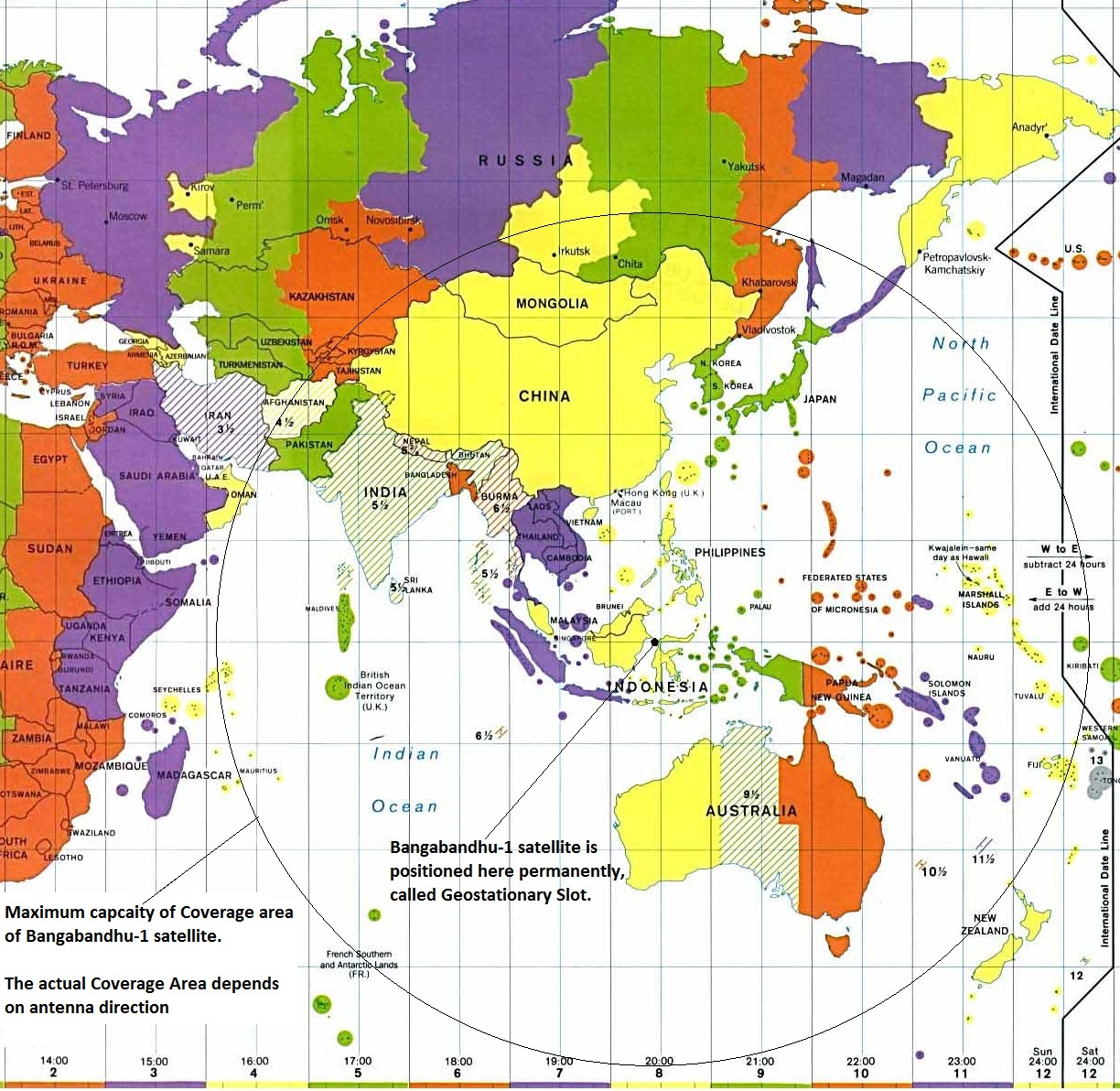
A coverage map illustrating how a geostationary telecommunications satellite provides service to a fixed region of Earth, using beam contours to show communication reach. Source.
Uses of Geostationary Orbits
The OCR specification emphasises that students should be able to define geostationary orbit and discuss telecommunications uses. These uses arise directly from the orbital stability and constant overhead position of the satellite.
Telecommunications
Geostationary satellites are widely used for:
Broadcast television, including satellite TV services requiring fixed dish installation.
International telephone relays, especially before the widespread development of fibre-optic undersea cables.
Internet data links, particularly in remote or rural areas where terrestrial connections are limited.
Satellite radio, supporting continuous reception over large areas.
Their fixed position ensures reliable uplink and downlink channels without the need for tracking equipment.
Meteorological Observation
Although not explicitly required by the specification, it is relevant to note that many weather agencies use geostationary satellites to provide:
Continuous cloud imaging
Monitoring of storm development
Tracking of large-scale atmospheric patterns
The constant view of the same hemisphere enables rapid updates, essential for forecasting and hazard awareness.
Navigation and Defence Systems
Several countries use geostationary satellites for strategic communication, secure data transmission, and navigation augmentation systems. These systems benefit from uninterrupted coverage of a region and high signal reliability.
Advantages and Limitations of Geostationary Orbits
Despite their extensive use, geostationary orbits present challenges. The great distance from Earth introduces:
Signal latency, usually around 240 ms one-way, affecting real-time communication.
High launch energy requirements, making placement and replacement costly.
Reduced coverage at high latitudes, as the satellite appears low on the horizon or becomes inaccessible.
Nonetheless, geostationary technology remains indispensable for modern infrastructure, particularly for broadcasting and global telecommunications, where its constant position and broad field of view offer unmatched practical advantages.
FAQ
A satellite must remain above the same point on Earth’s surface, which requires it to orbit in a plane that matches Earth’s rotational axis. The only plane that satisfies this is the equatorial plane.
If the orbit were inclined, the satellite would appear to oscillate north and south each day, preventing it from remaining fixed relative to the ground. This would make it unsuitable for stable telecommunications links.
Geostationary satellites are exposed to small but persistent forces that gradually alter their motion, including:
Gravitational pulls from the Moon and Sun
Non-uniformities in Earth’s gravitational field
Solar radiation pressure from sunlight
Residual orbital eccentricity or inclination
Orbit-keeping manoeuvres are routinely used to maintain the satellite in its assigned longitude and correct its inclination.
At high latitudes, a geostationary satellite appears extremely low on the horizon. This geometry weakens signal strength because signals must travel through more atmosphere and may be blocked by terrain or buildings.
Beyond roughly 70 degrees latitude, the satellite may drop below the visible horizon altogether, causing complete loss of coverage.
The geostationary belt is divided into carefully managed “orbital slots” assigned by international agreement, ensuring satellites maintain safe separation.
Operators maintain precise station-keeping procedures to hold satellites within tight longitude and inclination boundaries. Decommissioned satellites are moved to a “graveyard orbit” above GEO to prevent congestion.
The great distance of approximately 36,000 km reduces the received signal power significantly, so larger dishes are needed to achieve adequate signal gain.
Ground dishes also remain fixed in position, meaning they are optimised for a narrow, stable beam rather than tracking a moving satellite. This design compensates for weak incoming signals and helps maintain reliable communication links.
Practice Questions
Question 1 (2 marks)
State two conditions that must be satisfied for a satellite to be in a geostationary orbit.
Question 1 (2 marks)
Award 1 mark for each correct condition, up to 2 marks:
The satellite must orbit directly above the equator / in the equatorial plane. (1)
The satellite must travel in the same direction as Earth’s rotation (west to east). (1)
The satellite’s orbital period must be equal to Earth’s rotational period (approximately 24 hours / one sidereal day). (1)
The satellite must follow a circular orbit. (1)
(Any two for full marks.)
Question 2 (5 marks)
Explain why a geostationary orbit exists only at one specific orbital radius above Earth’s surface. In your answer, refer to Newton’s law of gravitation, the centripetal force requirement, and the orbital period needed for a geostationary orbit.
Question 2 (5 marks)
Award marks for the following points:
Earth’s gravitational force provides the centripetal force needed to keep the satellite in circular motion. (1)
Newton’s law of gravitation shows that gravitational force decreases with distance: F = GMm / r². (1)
Centripetal force required for circular orbit is mv² / r, and this must equal the gravitational force. (1)
Combining the gravitational and centripetal conditions leads to a specific relationship between orbital period and radius (T² proportional to r³). (1)
To have a period equal to Earth’s rotation, the satellite must therefore be at the unique radius that satisfies this relationship — approximately 36,000 km above Earth’s surface. (1)

