OCR Specification focus:
‘Gravitational potential equals work per unit mass from infinity to a point; zero at infinity.’
Gravitational potential describes how much work is needed to move a small mass within a gravitational field, providing a powerful way to understand energy changes and gravitational interactions.
Gravitational Potential in Gravitational Fields
Gravitational potential is a core idea in analysing gravitational interactions, especially when dealing with large separations in space where forces vary with distance. The OCR specification emphasises that gravitational potential is defined relative to infinity, where it is taken to be zero because gravitational influence becomes negligibly small at extremely large distances.
When discussing gravitational fields, it is essential to distinguish between gravitational field strength, which describes force per unit mass at a point, and gravitational potential, which describes energy per unit mass at a point.
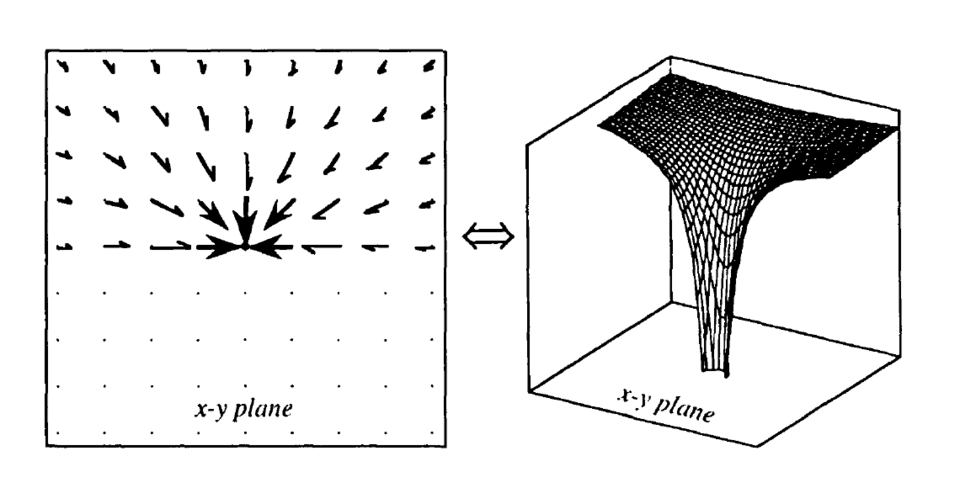
A two-dimensional slice of a gravitational force vector field is shown alongside its corresponding gravity-well surface, illustrating how a scalar gravitational potential relates to a vector force field. Each point in the vector field maps to a height on the potential surface, reinforcing the conceptual distinction between force and potential. The slope-force correspondence extends slightly beyond OCR requirements but supports deeper understanding. Source.
This distinction underpins many later applications, including satellite motion, escape velocity, and gravitational potential energy.
As the concept of gravitational potential is fundamentally linked to work, it provides a scalar way to track energy changes without explicitly dealing with vector forces at every stage.
Defining Gravitational Potential
The idea of gravitational potential arises naturally when considering how much energy is required to move a mass within a gravitational field. It gives a universal way to map the “landscape” of gravitational energy around a massive body.
Gravitational Potential: The work done per unit mass to bring a small test mass from infinity to a particular point in a gravitational field; its value is zero at infinity.
Because gravitational forces are always attractive, work must be done against the field to bring a mass closer to a gravitating body. This leads to gravitational potential being negative, reflecting the fact that a mass within a gravitational field is in a bound state. Students should understand that negative values do not indicate the absence of energy but rather that the system possesses energy lower than the reference point at infinity.
Gravitational potential is therefore a measure of how “deep” a point is in a gravitational well.
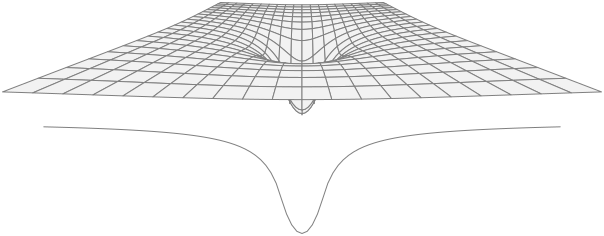
The upper panel illustrates a gravitational well, showing how positions closer to a mass lie deeper in potential. The lower graph displays gravitational potential as a function of distance, emphasising the increasingly negative values nearer the source. The space-time distortion reference exceeds OCR scope, but the Newtonian potential curve is directly relevant. Source.
The deeper the potential (i.e., the more negative), the more energy is required to remove a mass from that region and take it out to infinity.
Relationship Between Gravitational Potential and Work
Work provides the physical interpretation that makes potential meaningful. In gravitational contexts, work is done when a force moves an object through a distance. Because the gravitational force varies with distance from a mass, the work required must account for these changes.
Bringing a test mass from infinity involves gradually increasing gravitational attraction as the mass approaches the source. Thus, gravitational potential bundles all these small changes into one scalar quantity that expresses the total energy per kilogram associated with a location in the field.
A normal sentence is required before the equation block to comply with the formatting rules.
EQUATION
—-----------------------------------------------------------------
Gravitational Potential (V) = −GM / r
V = Gravitational potential (J kg⁻¹)
G = Universal gravitational constant (6.67 × 10⁻¹¹ N m² kg⁻²)
M = Mass of the gravitating body (kg)
r = Distance from the centre of mass (m)
—-----------------------------------------------------------------
Only point or spherically symmetric masses are treated using this expression at A-Level.
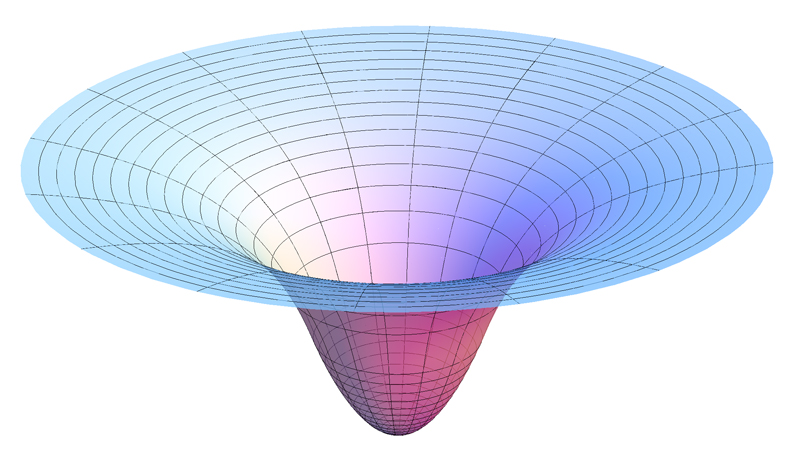
This visual shows gravitational potential for a homogeneous spherical mass, with potential becoming more negative toward the centre. The change in curvature at the surface highlights how potential behaves inside and outside such a body. The internal profile slightly exceeds OCR requirements but strengthens understanding of spherical mass models. Source.
This is consistent with Newtonian gravitation, where such masses can be modelled as though all their mass were concentrated at their centres. The negative sign reflects the convention that moving a mass inwards reduces its potential relative to infinity.
Key Features of Gravitational Potential
Understanding the behaviour of gravitational potential helps students interpret gravitational systems across many scales, from planetary surfaces to orbits.
Characteristics of Gravitational Potential
Scalar quantity: It has magnitude but no direction, making energy calculations simpler than force-based methods.
Negative values: Represent bound states within a gravitational field relative to zero potential at infinity.
Distance dependence: Potential becomes more negative as distance r decreases.
Universal reference point: Infinity provides a consistent zero point for all gravitational problems.
Per unit mass basis: Avoids the need to track specific masses until gravitational potential energy is calculated.
Visualising Gravitational Potential
Although potential is not a physical force, it is often visualised as a gravitational well. In this representation:
Steeper wells correspond to stronger gravitational fields.
Moving upwards in the well requires doing work against gravity.
Objects naturally “fall” to regions of lower (more negative) potential.
This metaphor reinforces the idea that gravitational potential represents the energy landscape through which objects move, offering intuitive insight into phenomena such as orbital binding, escape, and gravitational interactions between celestial bodies.
Practical Applications of Gravitational Potential
Gravitational potential forms the basis for many later ideas in the A-Level course. In particular, it helps describe:
Changes in gravitational potential energy, which follow directly from potential multiplied by mass.
Escape velocity, where an object must reach zero total energy to escape to infinity.
Orbital motion, where negative total energy ensures an object remains gravitationally bound.
Energy transfers during planetary motion, free fall, or astrophysical processes.
Understanding gravitational potential therefore equips students with a powerful tool for analysing energy in gravitational systems, providing insight that complements but extends beyond force-based descriptions.
FAQ
Gravitational potential refers to the work done per unit mass in bringing a test mass from infinity to a point in a gravitational field. It is an intrinsic property of the field created by a mass.
Gravitational potential energy depends on the specific mass placed in the field: potential energy equals mass multiplied by gravitational potential.
Thus, potential describes the field, while potential energy describes the energy of an object within that field.
A negative value indicates that work must be done to move a mass from a point in the field to infinity.
Because gravitational forces are attractive, a mass loses energy as it moves inward. To take the mass back out to infinity, energy must be supplied.
This required input of energy is expressed mathematically as a negative potential relative to the zero reference at infinity.
In Newtonian gravity, gravitational potential is always zero or negative because gravity is always attractive.
Positive gravitational potential would imply that no work is needed to remove an object to infinity—this cannot occur in an attractive-only field.
However, gravitational potential can become less negative as distance increases, approaching zero from below.
Inside a uniform-density sphere, gravitational potential varies differently compared with the outside region.
Key features:
It decreases smoothly towards the centre but with a different rate of change than outside the sphere.
Gravitational field strength decreases linearly to zero at the centre, but potential continues to become more negative until that point.
The transition at the surface is continuous, even though the slope changes.
Choosing zero potential at infinity standardises gravitational calculations and avoids ambiguity.
This reference point ensures that:
All potentials in a gravitational field are negative, reflecting the bound nature of masses.
Energy comparisons between different distances become straightforward.
Calculations of escape energy, orbital binding, and potential differences rely on a consistent baseline.
Changing the reference point would not affect physical outcomes, but it would complicate interpretation and comparisons.
Practice Questions
Question 1 (3 marks)
State what is meant by gravitational potential and explain why its value is taken to be zero at infinity.
Question 1 (3 marks)
Gravitational potential is the work done per unit mass to bring a small test mass from infinity to a point. (1 mark)
It is zero at infinity because gravitational influence becomes negligible at extremely large distances. (1 mark)
Infinity is taken as the standard reference point for gravitational potential. (1 mark)
Question 2 (6 marks)
A small test mass is moved from a point very far away from a planet to a point at distance r from the planet’s centre.
(a) Explain why the gravitational potential at distance r is negative.
(b) Describe the work that must be done to move the test mass from infinity to the point at distance r.
(c) The gravitational potential at this point is given by V = −GM / r. Use this expression to discuss how gravitational potential changes as the distance r increases, and relate this to the energy state of a mass in the gravitational field.
Question 2 (6 marks)
(a)
Gravitational potential is negative because gravity is attractive. (1 mark)
Work must be done against the gravitational field to bring the mass in from infinity to the point. (1 mark)
(b)
Work is required because the gravitational force pulls the mass towards the planet. (1 mark)
The total work done per unit mass in moving the test mass from infinity to distance r equals the gravitational potential at r. (1 mark)
(c)
From V = −GM / r, potential becomes less negative (increases) as r increases. (1 mark)
At very large r, V approaches zero, indicating that the mass becomes less bound to the planet’s gravity. (1 mark)
At small r, V is more negative, meaning the mass is more tightly bound and requires more energy to escape. (1 mark)

