Search coils allow experimental investigation of changing magnetic flux by converting variations in magnetic fields into measurable induced e.m.f., providing a powerful method for probing electromagnetic induction with accuracy.

Search Coils and Their Purpose

A search coil is a small coil of wire used to measure magnetic flux or magnetic flux density within a region of a magnetic field.

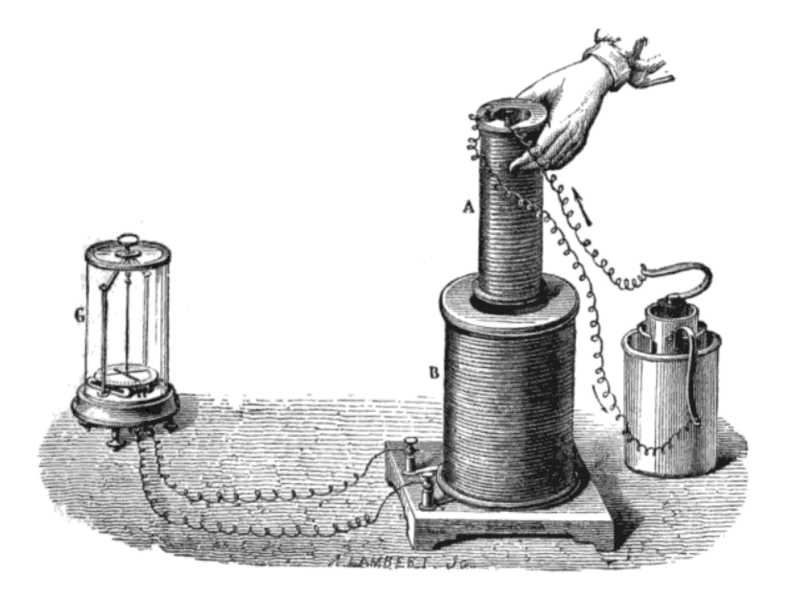
A historical diagram of Faraday’s induction experiment, showing a small current-carrying coil moved into and out of a larger coil connected to a galvanometer. As the magnetic flux through the larger coil changes, an induced current is detected. The image includes additional historical apparatus detail not required by the syllabus. Source.

Its operation relies on electromagnetic induction: when the magnetic flux through the coil changes, an e.m.f. is induced across its terminals. This makes the device ideally suited for examining how magnetic fields vary with time, position, or orientation.

A search coil is often connected to a voltmeter, data logger, or oscilloscope to record the induced e.m.f. Because the induced e.m.f. depends on the rate of change of flux, search coils provide a dynamic measurement tool rather than giving static field values directly.

Principles Underpinning Search Coil Measurements

At the heart of the technique is the relationship between induced e.m.f. and the rate of change of magnetic flux linkage.

EQUATION
—-----------------------------------------------------------------
Induced e.m.f. (𝓔) = − d(NΦ)/dt
𝓔 = Induced e.m.f. in volts
N = Number of turns on the search coil (no unit)
Φ = Magnetic flux through one turn, in webers
t = Time in seconds
—-----------------------------------------------------------------

This relationship shows that search coils respond to changes in flux rather than constant flux. Therefore, only time-varying fields or physically moved/rotated coils generate measurable signals. This dependence allows students to explore both steady magnetic fields through controlled movement and alternating fields directly.

A search coil’s sensitivity depends on its number of turns, cross-sectional area, and orientation. Increasing the number of turns or the area increases the total flux linkage, enhancing induced e.m.f. and improving measurement accuracy.

Construction and Design Considerations

Coil Structure

A typical search coil consists of:

• A tightly wound solenoid of fine copper wire

• A known number of turns (N)

• A rigid former that maintains a fixed coil area

• Insulated leads for connection to measuring instruments

Factors Affecting Sensitivity

• Area of the coil: Larger area increases flux linkage.

• Number of turns: More turns produce a proportionally larger induced e.m.f.

• Resistance of the coil and connecting leads: Lower resistance helps reduce signal loss.

• Orientation: Maximum flux linkage occurs when the plane of the coil is perpendicular to the magnetic field.

After defining these aspects, it becomes easier to understand how search coils function in practical laboratory settings.

Techniques for Using Search Coils to Investigate Magnetic Flux

1. Measuring Flux by Rotating a Coil

One common approach is to rotate a search coil within a magnetic field:

• The coil is mounted on an axle at the centre of the field region.

• As the coil rotates, the enclosed magnetic flux continuously changes.

• The induced e.m.f. can be monitored using an oscilloscope.

This method is particularly useful for investigating sinusoidal flux changes when rotation is uniform.

2. Inserting a Coil into a Varying Magnetic Field

Another widely used technique involves placing a stationary search coil into a region where the magnetic field varies with time:

• The search coil is inserted into the core of an a.c. electromagnet.

• When the flux through the electromagnet changes, an e.m.f. is induced in the coil.

• The induced voltage waveform mirrors the flux variation and can be studied in detail.

This technique allows direct examination of the relationship between alternating magnetic fields and induced voltages.

3. Using Search Coils to Map Magnetic Fields

Search coils can be used to map how flux density changes across space:

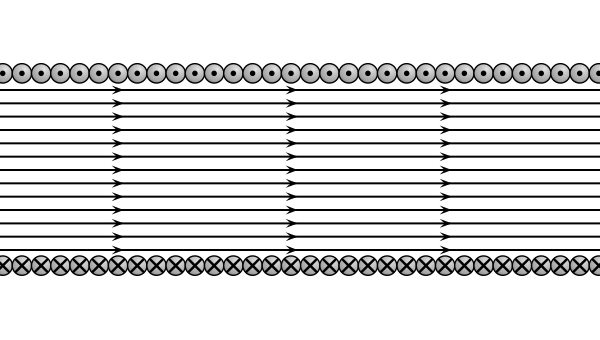
Diagram of a long, tightly-wound cylindrical coil producing an approximately uniform magnetic field inside. The magnetic field lines illustrate how flux passes through each turn of the coil. The diagram idealises the coil as infinitely long, which is slightly beyond the syllabus but still directly supportive of the concept. Source.

• Move the coil incrementally through the magnetic field region.

• Keep orientation constant to prevent unwanted angular variations.

• Record induced e.m.f. at each position.

• Convert induced e.m.f. values into flux density information using calibration data.

This provides a spatial profile of magnetic field strength and is especially valuable in solenoid or electromagnet analysis.

Calibration of Search Coils

To obtain accurate numerical measurements, search coils must be calibrated. Calibration involves comparing the induced e.m.f. generated in a known, well-controlled magnetic environment with the theoretical prediction.

Key Calibration Steps

• Place the coil within a region where B is known precisely.

• Apply a controlled, time-varying magnetic field.

• Measure the induced e.m.f. for several field strengths or rates of change.

• Plot induced e.m.f. against theoretical flux linkage to derive a consistent calibration factor.

This procedure ensures that subsequent experimental data obtained from unknown fields can be interpreted reliably.

Measuring a.c. Magnetic Fields

Search coils are especially effective for analysing alternating magnetic fields:

• When linked to an oscilloscope, they display the induced voltage waveform.

• The amplitude is proportional to the peak rate of change of flux.

• The frequency of the waveform equals the frequency of the alternating field.

This ability to visualise alternating field characteristics makes search coils a vital tool for exploring electromagnetic induction experimentally.