Understanding motion requires clear definitions of how position, time, and rate of change are described. This section establishes the fundamental kinematic quantities used to describe and analyse an object’s movement.

Displacement and Distance

Understanding Position and Motion

When analysing motion, we first need to specify how an object’s position changes. The term displacement represents both the magnitude and direction of this change, making it a vector quantity.

Displacement differs from distance, which measures only the total path length travelled, regardless of direction. Distance is therefore a scalar quantity, meaning it has magnitude but no direction.

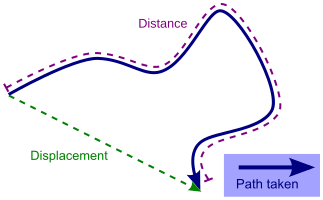
A schematic showing an object travelling along a curved path from a start to an end point. The distance is the length of the path, whereas the displacement is the straight-line vector from start to finish. This directly illustrates scalar versus vector descriptions of motion. Source.

In practical contexts, displacement provides a concise description of overall movement. For instance, if a runner completes a 400 m lap and finishes at the starting point, their distance travelled is 400 m but their displacement is zero, as there is no net change in position.

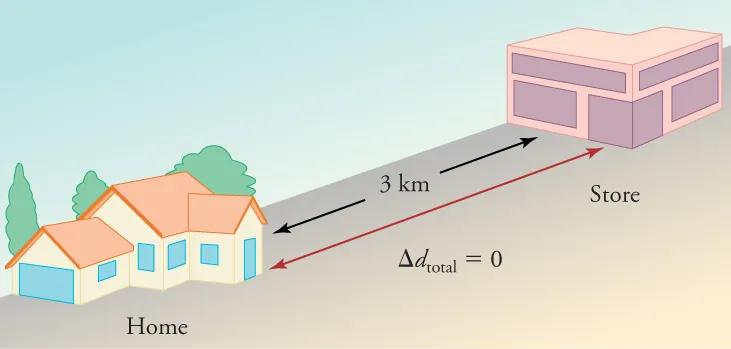
Figure 2.8 (OpenStax) depicts a house-to-store round trip in 30 minutes. The total distance travelled is 6 km (non-zero), but displacement for the round trip is zero, so the average velocity is zero while the average speed is 12 km h⁻¹. This neatly separates scalar speed from vector velocity. Source.

Speed

Quantifying Rate of Motion

Speed expresses how quickly an object covers distance. It provides a measure of the rate of change of distance with respect to time.

Speed is a scalar quantity because it does not involve direction. It can be measured in metres per second (m s⁻¹). There are two main forms of speed used in physics: instantaneous speed and average speed.

Instantaneous Speed

Instantaneous speed refers to the speed of an object at a specific moment in time. It can be obtained using short time intervals or data-logging equipment that captures rapid measurements. For example, a car’s speedometer shows its instantaneous speed.

Instantaneous speed is useful when motion is non-uniform, such as during acceleration or braking, where the object’s rate of motion varies continuously.

Average Speed

In contrast, average speed provides an overall description of motion over a finite period or distance. It is calculated by dividing the total distance travelled by the total time taken.

EQUATION
—-----------------------------------------------------------------
Average Speed (v_avg) = Total distance travelled / Total time taken
v_avg = d / t
v_avg = average speed (m s⁻¹)
d = distance (m)
t = time (s)
—-----------------------------------------------------------------

Average speed is particularly useful for describing journeys that involve varying speeds but where only the total distance and time are known. However, it gives no information about the direction of travel or changes in speed during motion.

Velocity

Defining Directional Rate of Change

Velocity extends the concept of speed by incorporating direction. It represents the rate of change of displacement with respect to time, making it a vector quantity.

This distinction is vital: two objects can have the same speed but different velocities if they move in opposite directions. For instance, travelling north at 10 m s⁻¹ and south at 10 m s⁻¹ represent identical speeds but opposite velocities.

Average and Instantaneous Velocity

Like speed, velocity can also be average or instantaneous. Average velocity considers total displacement over total time, while instantaneous velocity measures the rate of displacement change at a particular moment.

EQUATION
—-----------------------------------------------------------------
Average Velocity (v) = Displacement / Time
v = s / t
v = average velocity (m s⁻¹)
s = displacement (m)
t = time (s)
—-----------------------------------------------------------------

Instantaneous velocity can be determined from a displacement–time graph as the gradient (slope) of the curve at a given point. This graphical interpretation is essential for analysing motion that changes over time.

Acceleration

Rate of Change of Velocity

When an object’s velocity changes, either in magnitude or direction, it experiences acceleration. Acceleration quantifies how quickly velocity changes with respect to time.

Acceleration is a vector quantity because it depends on the direction of velocity change. If velocity increases in the same direction, acceleration is positive; if it decreases, it is negative (often referred to as deceleration).

Calculating Acceleration

EQUATION
—-----------------------------------------------------------------
Acceleration (a) = Change in velocity / Time taken
a = (v – u) / t
a = acceleration (m s⁻²)
v = final velocity (m s⁻¹)
u = initial velocity (m s⁻¹)
t = time (s)
—-----------------------------------------------------------------

This relationship applies to both uniform and non-uniform acceleration. In uniform acceleration, the rate of change of velocity remains constant, while in non-uniform motion, the acceleration varies over time.

Vector and Scalar Distinctions

Recognising Quantity Types

Understanding whether a quantity is a scalar or a vector is essential for correct analysis.

• Scalar quantities have magnitude only. Examples: distance, speed, time, mass, energy.

• Vector quantities have both magnitude and direction. Examples: displacement, velocity, acceleration, force.

When combining vector quantities, direction must always be considered, often using vector diagrams or component analysis. Scalars, on the other hand, can be added or subtracted through ordinary arithmetic.

Contextual Applications

Using Terms Precisely

In physics, using precise terminology is critical. Confusing displacement with distance or velocity with speed can lead to incorrect reasoning about motion. For instance:

• If an object returns to its starting point, displacement = 0 m, but distance > 0 m.

• A car moving at constant speed around a circular track has changing velocity because its direction constantly changes, hence it experiences centripetal acceleration.

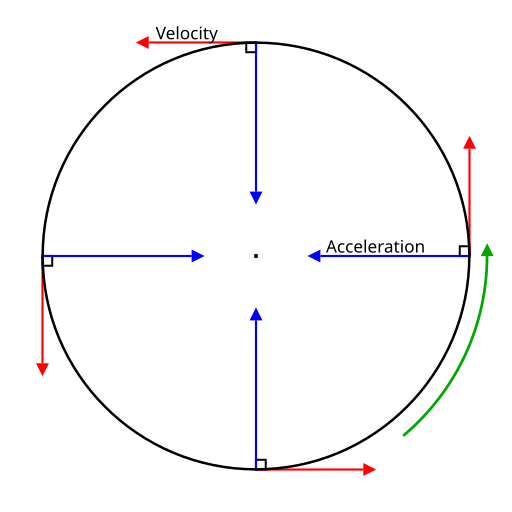
A vector diagram for uniform circular motion: velocity vectors are tangent to the circle, while acceleration vectors point towards the centre. This demonstrates that changing direction alone changes velocity, so acceleration is present even when speed is constant. Source.

These nuances illustrate why distinguishing between scalar and vector quantities is foundational to understanding motion.

Importance in Experimental Contexts

Accurate measurement and interpretation of displacement, speed, velocity, and acceleration underpin experimental physics. Devices such as light gates, data loggers, and motion sensors enable precise capture of these quantities. In every case, understanding what each term represents ensures that data are interpreted correctly and physical conclusions are sound.