Elastic potential energy describes the energy stored in materials when they are stretched or compressed elastically, allowing them to return to their original shape when released.

Understanding Elastic Potential Energy

When a spring or wire is deformed by applying a force, work is done on the material. If the deformation is elastic, this work is stored as elastic potential energy within the material’s atomic structure. This energy can be completely recovered when the force is removed, provided the material has not exceeded its elastic limit.

Elastic potential energy arises from the stretching or compressing of interatomic bonds, which behave like tiny springs. As the atoms are displaced from their equilibrium positions, a restoring force develops, tending to return them to equilibrium. This is the microscopic origin of Hookean behaviour.

Relationship Between Force and Extension

The force-extension relationship for a spring or wire within its elastic limit is governed by Hooke’s Law, which states that the force is directly proportional to the extension.

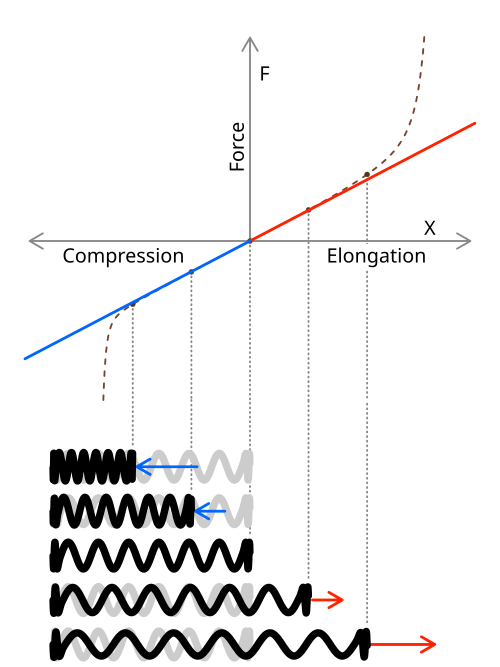
Hooke’s law in the elastic region: force is directly proportional to extension, with gradient equal to the spring constant k. The plot passes through the origin and illustrates both extension and compression. Dashed non-linear parts indicate behaviour beyond ideal proportionality (extra detail not required by the OCR subsubtopic). Source.

EQUATION
—-----------------------------------------------------------------
Hooke’s Law (F = kx)
F = Force applied to the spring (N)
k = Force constant or spring constant (N m⁻¹)
x = Extension of the spring (m)
—-----------------------------------------------------------------

The force constant (k) is a measure of stiffness. A higher k means the material or spring is stiffer and requires more force to produce a given extension.

Work Done and Energy Stored

The work done to stretch or compress an elastic object is equal to the energy stored as elastic potential energy. The force-extension graph for an elastic material is typically a straight line through the origin, indicating proportionality between force and extension. The area under this line represents the work done, which corresponds to the energy stored.

EQUATION
—-----------------------------------------------------------------
Elastic Potential Energy (E = ½Fx)
E = Elastic potential energy (J)
F = Force applied (N)
x = Extension (m)
—-----------------------------------------------------------------

Because force increases linearly with extension, the average force over the stretching process is ½F, leading to the factor of ½ in the expression. This equation is particularly useful when the final force is known but not the spring constant.

Energy in Terms of the Spring Constant

By substituting Hooke’s law (F = kx) into the previous relation, we obtain an alternative expression that depends only on the spring constant and the extension:

EQUATION
—-----------------------------------------------------------------
Elastic Potential Energy (E = ½kx²)
E = Elastic potential energy (J)
k = Force constant (N m⁻¹)
x = Extension (m)
—-----------------------------------------------------------------

This form is often more convenient when the spring constant is known and avoids the need to measure force directly. It also clearly shows that energy increases with the square of the extension, meaning doubling the extension quadruples the stored energy.

Interpreting the Energy–Extension Relationship

The quadratic dependence of energy on extension has several key implications:

• The energy stored increases rapidly with larger extensions, provided the material remains within the elastic limit.

• When plotted on a graph of energy (E) against extension (x), the relationship forms a parabolic curve.

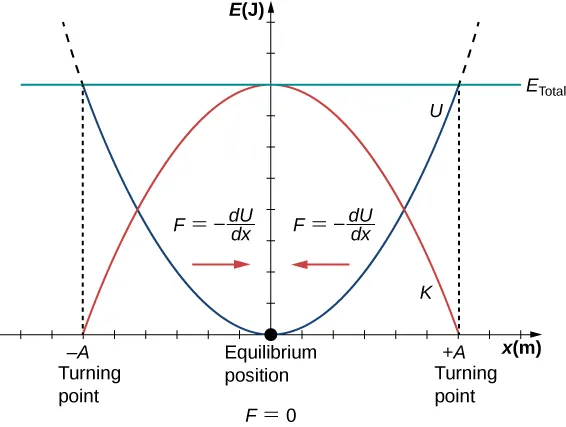
Potential energy U = ½kx² increases with the square of extension, giving a parabolic E–x graph. The equilibrium at x = 0 is the minimum of the potential well. The figure also indicates turning points where energy is entirely potential. Source.

• The point where the material reaches its limit of proportionality marks the boundary between linear elastic behaviour and non-linear deformation, beyond which Hooke’s law no longer applies.

Beyond this limit, additional work done does not increase recoverable elastic energy in the same way, as some of the energy is used to cause plastic deformation—permanent changes in the material’s structure.

Elastic Potential Energy in Wires and Springs

The same principles apply whether the object is a coiled spring, a metal wire, or another elastic component:

• For a spring, the extension is macroscopic and easily measured.

• For a wire, the extensions are typically much smaller and require precise measurement using instruments such as a micrometer screw gauge and optical lever setup.

In both cases, the work done per unit volume relates to the strain energy density, which provides a useful measure of the energy stored per cubic metre of material. However, for this specification level, it is sufficient to understand energy storage in terms of total force and extension.

Energy Transfer and Conservation

When a spring or wire is stretched elastically:

1. Mechanical work is done by the external force.

2. This work is converted into potential energy within the material’s atomic structure.

3. On release, the stored energy is converted back into kinetic or gravitational potential energy, depending on the situation.

This process obeys the principle of conservation of energy, where the total energy before and after deformation remains constant, assuming no energy is dissipated as heat or sound.

Experimental Verification

To verify the relationship between force, extension, and elastic potential energy:

• Gradually apply known weights to a spring or wire.

• Measure the resulting extensions.

• Plot a force-extension graph; the straight-line portion confirms Hooke’s law.

• Determine the area under the graph to calculate the energy stored for different loads.

Key practical considerations include:

• Ensuring measurements remain within the elastic limit to avoid permanent deformation.

• Taking multiple readings for accuracy.

• Avoiding oscillations when applying loads.

Real-World Relevance

Elastic potential energy is fundamental to many physical systems:

• Mechanical clocks and toys rely on wound springs.

• Vehicle suspensions store and release energy for a smoother ride.

• Bungee cords and trampolines depend on controlled energy storage and release.

In engineering contexts, understanding how materials store elastic energy is essential to ensure safety and performance. Exceeding elastic limits can lead to structural failure or fatigue, so precise calculation and control of elastic potential energy is critical.