OCR Specification focus:
‘Define Young modulus as stress ÷ strain; determine E experimentally for a metal wire.’
The Young modulus quantifies how stiff a material is by relating stress to strain within the elastic region of deformation. It enables comparisons of material rigidity and structural performance.
Definition and Concept of Young Modulus
The Meaning of Young Modulus
The Young modulus (E) is a measure of the stiffness of a material — that is, how much it resists deformation under tensile or compressive stress. It applies only within the elastic region, where the material returns to its original shape after the load is removed.
Young Modulus (E): The ratio of stress to strain for a material within its elastic limit.
In other words, the Young modulus provides a constant of proportionality between stress (force per unit area) and strain (extension per unit length), assuming linear elastic behaviour. It is an intrinsic property of a material, independent of the sample’s shape or size.
Relationship Between Stress and Strain
EQUATION
—-----------------------------------------------------------------
Young Modulus (E) = Stress / Strain
E = σ / ε
σ (Stress) = Force (F) ÷ Cross-sectional area (A) (Unit: pascal, Pa)
ε (Strain) = Extension (ΔL) ÷ Original length (L₀) (No unit)
—-----------------------------------------------------------------
This relationship demonstrates that for a given stress, a material with a higher Young modulus will experience a smaller strain — it is stiffer. Conversely, a material with a low Young modulus deforms more easily under the same stress.
The gradient of the initial linear region of a stress–strain graph equals the Young modulus EEE.
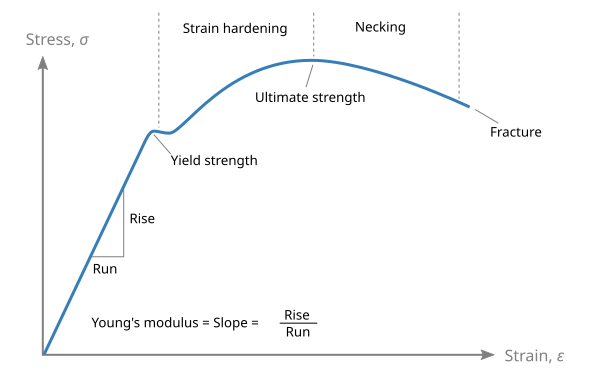
Schematic stress–strain curve for a ductile material. The initial straight-line region is linear elastic; its gradient is the Young modulus (E). Features beyond the syllabus focus (yield/UTS/necking) are shown but can be ignored for determining E. Source.
Elastic Behaviour and the Elastic Limit
Elastic Region and Hookean Behaviour
Within the elastic region, a material follows Hooke’s law, meaning stress is directly proportional to strain. The constant of proportionality is the Young modulus. Once the elastic limit is exceeded, the material behaves plastically — permanent deformation occurs, and the relationship between stress and strain no longer holds.
Elastic deformation: The material returns to its original length once the load is removed.
Plastic deformation: The material is permanently stretched beyond the elastic limit.
It is essential to ensure that when determining E, all measurements are taken while the material remains within the linear (proportional) section of the stress–strain curve.
Measuring the Young Modulus Experimentally
Overview of the Experiment
The Young modulus of a metal wire can be determined by measuring the extension produced by known forces, and calculating the corresponding stress and strain.
A typical experiment uses a long, thin wire (such as copper or steel) clamped at one end with a weight hanger attached to the other. The setup allows accurate measurement of small extensions when forces are applied incrementally.
Apparatus Required
Metal wire (e.g. copper, steel, or nichrome) of known diameter.
Micrometer screw gauge to measure the wire’s diameter at several points.
Metre ruler or travelling microscope to measure the wire’s original length.
Weight hanger and slotted masses to apply known forces.
Marker or pointer attached to the wire to measure extensions precisely.
Experimental Procedure
Measure the wire’s original length (L₀):
Secure the wire at the top using a rigid clamp and measure its length from the clamp to the marker using a ruler or tape measure.
Determine the cross-sectional area (A):
Measure the diameter at several points along the wire using a micrometer screw gauge.
Calculate the mean diameter and use
A=πd2/4A = πd² / 4A=πd2/4 to find the area.
Measure the wire’s diameter with a micrometer screw gauge at several positions along the wire and calculate the mean radius.
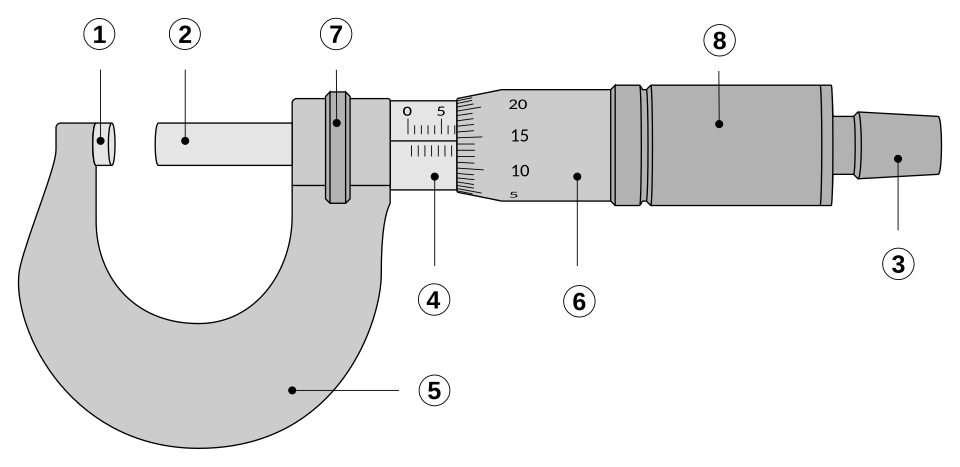
Labelled parts of an outside micrometer used to measure wire diameter with 0.01 mm precision. Understanding the anvil–spindle contact and thimble/sleeve scales reduces reading and zero-error mistakes. The illustration also shows a sample reading; this extra detail is beyond the OCR requirement but helpful. Source.
Apply forces incrementally:
Add masses to the hanger to apply known forces (F = mg).
Record the corresponding extensions (ΔL) using the marker and scale.
Allow time for the wire to settle each time to avoid creep errors.
Remove loads gradually:
Note whether the wire returns to its original length to confirm the elastic limit has not been exceeded.
Repeat measurements for accuracy:
Take several readings for each load and average them to reduce random errors.
Data Analysis and Calculation
From the measurements:
Stress is calculated using σ = F / A.
Strain is calculated using ε = ΔL / L₀.
Plot a graph of stress (y-axis) against strain (x-axis).
The gradient of the straight-line portion of this graph gives the Young modulus (E).
EQUATION
—-----------------------------------------------------------------
Gradient Method: E = Δσ / Δε
E = (Change in stress) ÷ (Change in strain)
—-----------------------------------------------------------------
This graphical method offers an accurate value since it averages out measurement uncertainties and eliminates the need for intermediate calculations of extension per force increment.
Precision, Errors and Safety Considerations
Sources of Uncertainty
To ensure high precision and reliability:
Take diameter measurements at several orientations to account for wire imperfections.
Use small incremental loads to remain within the elastic region.
Avoid sudden jerks or overloading that might introduce plastic deformation.
Record extensions with a travelling microscope for improved precision
Ensure temperature stability, since heating affects material dimensions and elasticity.
Safety Precautions
Use safety goggles, as a wire under tension can snap suddenly.
Place a protective screen around the wire.
Ensure the weights are secure and added gently to prevent shock loading.
Interpreting Results and Comparing Materials
Material Stiffness and Structural Application
A higher Young modulus indicates a stiffer material. For instance:
Steel has a large E value, making it ideal for structural frameworks and cables.
Copper and brass have lower values, making them suitable for flexible electrical wiring.
Engineers and designers use the Young modulus to select materials for applications that demand specific stiffness, flexibility, or load-bearing properties.
Behaviour Beyond the Elastic Limit
Once the load exceeds the elastic limit, the stress–strain curve deviates from linearity, and E no longer applies. The material then undergoes plastic deformation, leading ultimately to necking and fracture. This is beyond the region considered for determining the Young modulus but illustrates the transition from elastic to plastic behaviour in real materials.
FAQ
Accuracy can be influenced by:
Temperature changes, which alter the material’s dimensions and elastic properties.
Measurement precision, particularly in the diameter — a small error in diameter causes a large error in area and hence stress.
Wire imperfections, such as kinks or non-uniform thickness, which create inconsistent strain along the length.
Instrument calibration, ensuring micrometers, rulers, and vernier scales are correctly zeroed before use.
Environmental vibrations or drafts can also cause small fluctuations in the measured extension.
A long, thin wire produces a larger measurable extension for a given force, increasing experimental sensitivity and reducing percentage uncertainty.
If the wire were short or thick, the same force would cause only a tiny extension, which would be difficult to detect accurately.
However, the wire must not be so thin or long that it risks snapping under its own weight or due to small additional loads.
As temperature increases, the atoms vibrate more vigorously, weakening interatomic bonds and making the material easier to stretch.
This results in a lower Young modulus, meaning the metal becomes less stiff.
At very low temperatures, the opposite occurs — atomic vibrations reduce, the bonds strengthen, and the material’s stiffness increases.
This temperature dependence is significant in precision engineering and aerospace applications.
The Young modulus is a material constant describing the ratio of stress to strain within the elastic region. It applies only while the relationship is linear and reversible.
The elastic limit, on the other hand, is a point on the stress–strain curve beyond which permanent deformation begins.
In short, the Young modulus defines how the material behaves elastically, while the elastic limit defines where that behaviour stops.
Yes, in some materials the Young modulus can differ for tensile and compressive stresses.
For most metals, the difference is negligible because atomic bonding is largely symmetrical.
However, in anisotropic or composite materials (e.g. wood, carbon fibre), internal structure causes the material to resist stretching and compression differently.
This directional dependence is important when designing components that experience both tension and compression, such as beams and aircraft wings.
Practice Questions
Question 1 (2 marks)
A copper wire of original length 2.0 m and diameter 0.80 mm extends by 1.0 mm when a force is applied. Define the Young modulus and state its SI unit.
Mark Scheme:
1 mark: Correct definition — “The Young modulus is the ratio of stress to strain for a material within its elastic limit.”
1 mark: Correct SI unit — “Pascal (Pa) or N m⁻².”
Question 2 (5 marks)
A student investigates the Young modulus of a steel wire using a Searle’s apparatus. The wire has a measured diameter of 0.50 mm and a length of 1.5 m. The student adds weights in 1.0 N increments and records the extension using a vernier scale.
(a) Describe how the student should obtain an accurate value for the Young modulus from this experiment.
(b) Explain how the student can reduce errors and ensure the results are valid.
Mark Scheme:
(a) (3 marks)
1 mark: Measure original length (L) of wire between the fixed points using a ruler or metre stick.
1 mark: Determine cross-sectional area (A) by measuring wire diameter in several places with a micrometer and calculating A = πd² / 4.
1 mark: Apply known forces (F = mg), measure corresponding extensions (ΔL), calculate stress (F/A) and strain (ΔL/L), and obtain E from the gradient of a stress–strain graph.
(b) (2 marks)
1 mark: Keep the load increments small to remain within the elastic limit and avoid plastic deformation.
1 mark: Reduce errors by averaging diameter readings, using a travelling microscope or vernier scale for precise extension measurement, and allowing time for the wire to settle after each load is added.

