OCR Specification focus:
‘Recognise that work done stretching is the area under the force–extension (or compression) graph.’
When a force stretches or compresses a material, energy is transferred and stored within it. Understanding how this work done relates to the force–extension graph is essential for analysing elastic behaviour and calculating elastic potential energy in materials.
The Concept of Work in Stretching and Compression
When a material such as a spring, wire, or rubber band is stretched, work is done by the applied force to change its shape. This work is stored as elastic potential energy if the material remains within its elastic limit — meaning it will return to its original form once the force is removed.
The total work done can be visualised and calculated using the area under the force–extension graph.
Understanding the Force–Extension Graph
A force–extension graph plots the applied force (F) on the vertical axis against the extension (x) on the horizontal axis.
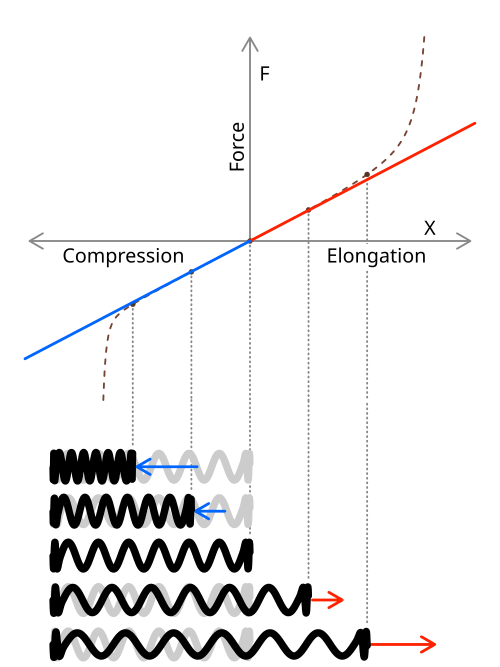
A labelled Hooke’s law diagram: linear F–x relation with extension (red) and compression (blue) indicated; slope gives k. The area under the curve up to a chosen x corresponds to work done. Note that the dashed “real spring” and extreme-deformation remarks shown on the source page exceed the OCR focus and can be disregarded for this subsubtopic. Source.
In the elastic region, the relationship between force and extension is linear, following Hooke’s law: force is directly proportional to extension. Beyond this region, the material may no longer behave elastically, and the graph becomes non-linear.
Key features of the graph include:
The origin, representing zero force and zero extension.
The linear (proportional) region, where F ∝ x.
The elastic limit, marking the point beyond which the material will not return to its original length.
The non-linear region, where plastic deformation or permanent change occurs.
Work Done and Energy Representation
The work done on a spring or material is the energy transferred to it through stretching or compressing. On the force–extension graph, this energy corresponds to the area under the curve.
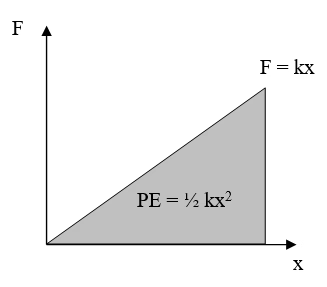
A linear spring obeying Hooke’s law has a straight-line force–extension graph. The shaded triangular area under the curve represents the work done (and elastic potential energy stored) up to extension x. This figure focuses on the geometric interpretation required by OCR; minor surrounding page text on calculus is extra context not required by the syllabus. Source.
This relationship holds true because each small increase in extension requires an incremental amount of work, and summing all these infinitesimal contributions gives the total energy stored.
EQUATION
—-----------------------------------------------------------------
Work Done (W) = Area under Force–Extension Graph
Alternatively, for a linear spring obeying Hooke’s law:
Elastic Potential Energy (E) = ½ × F × x
E = ½ × k × x²
F = restoring force (newtons, N)
x = extension or compression (metres, m)
k = spring constant or force constant (newtons per metre, N m⁻¹)
—-----------------------------------------------------------------
These expressions are equivalent, since F = kx within the elastic region.
Relationship Between Force, Extension, and Energy
When the force increases uniformly with extension, the average force over the extension is ½F (assuming zero force at zero extension). Hence, the area under the straight-line portion of the graph — a right-angled triangle — gives the total work done or energy stored in the material.
For non-linear materials (such as rubber or polythene), the curve is not straight, so the area under the curve must be determined using geometric approximation or integration.
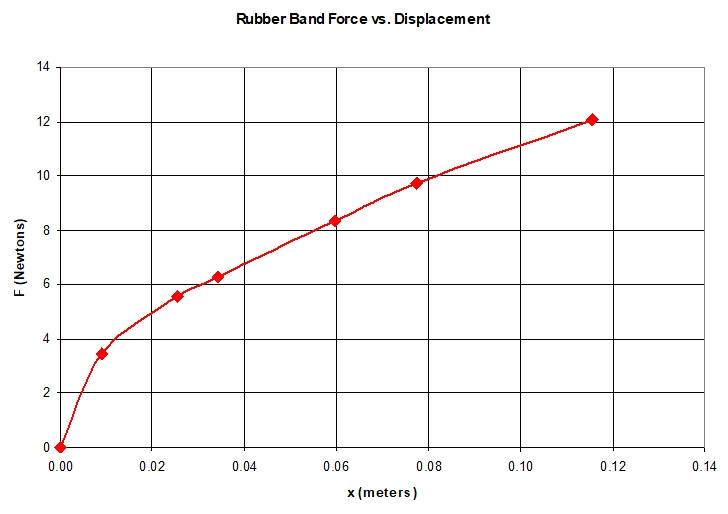
A measured force–extension curve for a rubber band demonstrating non-linear elasticity. The area under the curve still equals the work done to stretch the band, but the shape is not triangular. Any extra curve-fitting details on the source page exceed OCR’s requirement and can be ignored here. Source.
This approach captures variations in the force required at different extensions.
Distinguishing Between Stretching and Compression
The same principles apply for both stretching and compression:
Stretching: Work is done on the material to increase its length.
Compression: Work is done on the material to reduce its length.
In both cases, the energy stored equals the area under the respective curve, although compressive systems (such as springs in compression) may have slightly different elastic properties due to material geometry or frictional effects.
Elastic Potential Energy and the Elastic Limit
As long as the material remains within its elastic limit, the energy stored is recoverable — when the load is removed, the material releases the stored energy and returns to its original length.
However, if the material is stretched beyond the elastic limit, some of the work done goes into permanent deformation, and not all energy is recovered. This leads to energy dissipation as heat or structural change, visible in a hysteresis loop if the loading and unloading curves differ.
Experimental Interpretation
In a laboratory investigation, students might measure the extension of a spring or wire as incremental forces are applied. By plotting force against extension:
The shape of the graph reveals whether Hooke’s law is obeyed.
The area under the curve (up to a certain force) quantifies the energy stored in the material.
This area can be calculated:
Geometrically, if the relationship is linear (area of a triangle = ½ × base × height).
Numerically or via integration, if the curve is non-linear.
Such measurements reinforce the connection between mechanical work, elastic energy, and graphical representation.
Energy Stored and Released: The Physical Perspective
At the atomic level, stretching a material involves separating atoms or molecules slightly within their interatomic potential wells. The restoring forces between them act to bring the structure back to equilibrium. The work done in displacing these atoms is stored as elastic potential energy, which can later be released when the material returns to its original form.
When the force is removed:
If deformation is elastic, energy is fully released.
If deformation is plastic, some energy is lost due to bond rearrangement or frictional heat.
This microscopic model explains why elastic materials efficiently store and return energy, while plastic materials absorb it irreversibly.
Comparing Different Materials
Different materials exhibit distinct force–extension characteristics, influencing the area under their graphs:
Metals (e.g., copper, steel): Linear elastic region followed by a yield region; large area indicates significant energy absorption before breaking.
Rubber: Non-linear but fully recoverable; large hysteresis loop due to internal friction and molecular rearrangements.
Polythene: Low stiffness; reaches plastic deformation quickly; area under the curve shows lower energy storage before failure.
By comparing these areas, one can infer which materials are more resilient or energy-efficient for applications such as shock absorbers, bungee cords, or springs.
Key Points Summary for OCR Focus
Students must be able to:
Recognise that the work done in stretching or compressing a material is represented by the area under the force–extension (or compression) graph.
Understand how this area relates directly to the energy stored in the material.
Identify differences between linear (Hookean) and non-linear materials when interpreting the graph.
Appreciate that the shape of the graph reflects the mechanical behaviour and energy characteristics of the material under load.
FAQ
If the graph is a straight line through the origin, the material behaves elastically within that region, following Hooke’s law (F ∝ x).
Once the graph begins to curve and no longer returns to the origin when the force is removed, the material has entered plastic deformation. This means permanent structural changes occur and some of the work done is not recoverable as elastic potential energy.
When a material such as rubber is stretched and released, its loading and unloading curves form a hysteresis loop.
The area enclosed by this loop represents energy lost, often as heat due to internal molecular friction. This explains why rubber bands can feel warm after being stretched repeatedly — not all of the work done is returned as mechanical energy.
Yes. If a spring is stretched beyond its elastic limit, part of the work done goes into permanent deformation rather than storing recoverable energy.
In this case:
Some energy becomes internal energy, increasing temperature.
The spring does not return fully to its original shape.
Thus, only deformation within the elastic region results in stored elastic potential energy that can be released again.
Although Hooke’s law gives a proportional relationship between force and extension, the force must increase gradually as the spring stretches.
This occurs because:
Each small additional extension requires more force to balance the spring’s restoring force.
The total work done is found from the average force, represented by the area under the curve, rather than a single constant force.
Hence, even in the linear region, the applied force changes continuously with extension.
For a non-linear material, the force changes unevenly with extension, so the area under the curve must be determined using integration.
Mathematically, the total work done W equals the integral of F with respect to x between the limits of extension:
W = ∫ F dx
This gives the precise area under the graph. In experimental practice, students approximate this by dividing the curve into small segments, finding the area of each, and summing them to estimate total work done.
Practice Questions
Question 1 (2 marks)
A student stretches a spring that obeys Hooke’s law and records the following data:
Maximum force applied: 4.0 N
Extension at this force: 0.08 m
Using the force–extension relationship, calculate the work done in stretching the spring. State the unit of your answer.
Question 1 (2 marks)
Correct use of relationship for work done or elastic potential energy: W = ½ × F × x (1 mark)
Substitution and correct numerical answer: W = ½ × 4.0 × 0.08 = 0.16 J (1 mark)
Question 2 (5 marks)
A student investigates the behaviour of two different materials: a steel spring and a rubber band. Both are stretched and their force–extension graphs are plotted on the same axes.
(a) Explain how the work done in stretching each material can be determined from the graphs.
(b) Describe the differences you would expect to see in the shapes of the two curves and what these differences reveal about the materials’ properties.
(c) Discuss what happens to the energy stored in each material when the force is removed.
Question 2 (5 marks)
(a)
States that work done (or energy stored) equals the area under the force–extension graph (1 mark)
Recognises that for a linear spring, the area is a triangle (½ × base × height) (1 mark)
(b)
Identifies that the steel spring shows a straight-line (linear) region obeying Hooke’s law, while the rubber band shows a curved, non-linear graph (1 mark)
Explains that this indicates the steel behaves elastically up to its limit, while the rubber’s stiffness changes with extension (1 mark)
(c)
States that the steel spring releases nearly all stored energy on unloading (elastic behaviour), whereas the rubber band shows energy loss (hysteresis loop, heat dissipation) (1 mark)

