OCR Specification focus:
‘Microscopic carrier speed and density link to macroscopic current via I = A n e v.’
The relationship between macroscopic current and microscopic motion reveals how individual charge carriers combine to produce measurable electric current. By connecting atomic-level motion to circuit-scale current, we can understand conductivity, material properties, and how different substances carry charge.
The Microscopic View of Current
Charge Carriers and Motion
In a conductor, electric current arises from the collective motion of charge carriers. These are typically free electrons in metals or ions in electrolytes and semiconductors. When no potential difference is applied, these carriers move randomly, producing no net flow of charge.
When a potential difference (voltage) is applied across a conductor, an electric field is established within it. This field exerts a force on the charge carriers, causing them to drift slowly in one direction. Though the random thermal motion remains very fast, the average displacement in a specific direction per unit time — the mean drift velocity — is relatively slow.
Relating Microscopic Motion to Macroscopic Current
Understanding the Connection
The macroscopic electric current measured in amperes (A) is a bulk property that emerges from the microscopic movement of countless charge carriers. The relationship between the current (I) and the motion of these carriers is given by the continuity equation:
EQUATION
—-----------------------------------------------------------------
Electric Current (I) = A n e v
A = Cross-sectional area of the conductor (m²)
n = Number density of charge carriers (m⁻³)
e = Charge of each carrier (C)
v = Mean drift velocity (m s⁻¹)
—-----------------------------------------------------------------
This equation links microscopic quantities (n, e, v) to a macroscopic measurable (I).
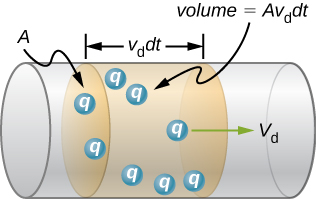
All charges within the shaded volume A vd dtA\,v_d\,dtAvddt leave the section in time dtdtdt, giving charge flow per second I=nqAvdI = n q A v_dI=nqAvd. The diagram also labels vdv_dvd and AAA to emphasise the physical meaning of each factor. (Includes brief context on current density in nearby text on the page.) Source.
It expresses that the total current is the product of the charge per carrier, how many carriers move through a unit volume, their average velocity, and the size of the conductor through which they move.
Visualising the Flow of Charge
Imagine the conductor as a tube filled with charge carriers. Each second, a number of these carriers pass through any cross-section of the conductor.
The number of carriers per cubic metre is n.
The cross-sectional area available for flow is A.
The drift velocity (v) determines how far each carrier moves per second.
Multiplying these quantities gives the number of carriers crossing the section each second, and multiplying by the charge per carrier (e) gives the total charge per second, i.e., the current (I).
Significance of Each Quantity
Number Density (n)
Number Density (n): The number of charge carriers per unit volume of a material (m⁻³).
The value of n depends strongly on the material: metals have high n, semiconductors moderate, and insulators extremely low. A higher n means more charge carriers available to contribute to the current, resulting in a higher possible current for a given drift velocity.
Mean Drift Velocity (v)
Mean Drift Velocity (v): The average velocity of charge carriers moving under an electric field, superimposed on their random thermal motion.
Although individual electrons move randomly at very high speeds, their net drift caused by the electric field is tiny — often less than 1 mm/s — due to frequent collisions with atoms.
Linking Microscopic and Macroscopic Perspectives
The Role of Collisions and Resistivity
At the microscopic level, electrons accelerate in the electric field but are continually scattered by lattice ions. These collisions limit their average velocity, creating resistance to current flow. The balance between acceleration due to the field and deceleration due to collisions determines the steady-state drift velocity.
Because I = A n e v, any change in drift velocity directly alters the current, provided A, n, and e remain constant. Conversely, for a fixed current, the drift velocity must change if the cross-sectional area or number density changes.
Microscopic Insight into Current Density
The relationship can also be described using current density (J), which represents current per unit cross-sectional area:
EQUATION
—-----------------------------------------------------------------
Current Density (J) = n e v
J = Current per unit area (A m⁻²)
n = Number density (m⁻³)
e = Charge per carrier (C)
v = Mean drift velocity (m s⁻¹)
—-----------------------------------------------------------------
From this, I = J × A, linking the microscopic expression directly to measurable current.
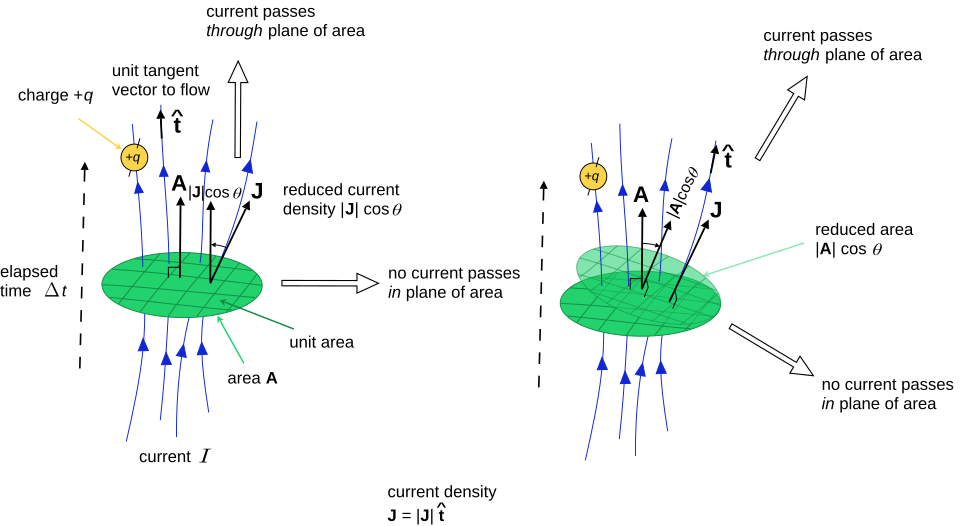
Schematic showing the relation between charge flow and current density J\mathbf{J}J in a conductor’s cross-section. The diagram emphasises that J=nqvd\mathbf{J} = n q \mathbf{v}_dJ=nqvd locally, which scales up to I=JAI = J AI=JA for a uniform cross-section. (This image focuses on J\mathbf{J}J; it does not derive I=nqAvdI = n q A v_dI=nqAvd explicitly.) Source.
This shows that materials with higher carrier density or faster drift speed exhibit greater current density for the same electric field.
Microscopic Interpretation of Conductivity
The equation I = A n e v forms the foundation for understanding electrical conductivity (σ). Conductivity measures how easily charge flows through a material and depends on both n (how many carriers are available) and v (how fast they move). The drift velocity itself depends on the mobility (μ) of the carriers and the electric field (E) through:
EQUATION
—-----------------------------------------------------------------
Drift Velocity (v) = μ E
v = Mean drift velocity (m s⁻¹)
μ = Mobility of charge carriers (m² V⁻¹ s⁻¹)
E = Electric field strength (V m⁻¹)
—-----------------------------------------------------------------
Substituting this into I = A n e v gives an expression that connects current, electric field, and material properties, reinforcing that macroscopic current arises directly from microscopic carrier dynamics.
Interpreting the Equation Practically
To summarise the physical meaning:
A larger cross-sectional area (A) allows more carriers to pass through simultaneously.
A higher number density (n) means more carriers per unit volume, increasing current.
A greater charge (e) per carrier directly scales up the current.
A higher drift velocity (v) indicates carriers are moving faster, transporting charge more quickly.
Together, these determine how materials and their internal microscopic properties manifest as measurable macroscopic electric current in circuits and devices.
FAQ
The mean drift velocity depends on several factors:
Current (I): Higher current requires a higher drift velocity if the number density and cross-sectional area remain constant.
Cross-sectional area (A): A thinner wire means charge carriers must move faster to maintain the same current.
Number density (n): Materials with more available charge carriers need less drift velocity for the same current.
Temperature: Increasing temperature usually increases lattice vibrations, leading to more collisions and a smaller drift velocity for a given field strength.
Although currents in household circuits are large, the number of charge carriers in metals is enormous — typically around 10²⁸ per cubic metre.
Because so many electrons move simultaneously, each individual electron only needs to move very slowly to create a large total current.
Typical drift velocities are fractions of a millimetre per second, even when the electron thermal speeds (random motion) are millions of metres per second.
When a potential difference is applied, the electric field propagates through the conductor almost instantaneously at a significant fraction of the speed of light.
This field causes electrons everywhere in the conductor to start drifting almost simultaneously.
As a result, the current appears continuous even though individual electrons move slowly — much like pushing one end of a tube filled with marbles causes all marbles to move at once.
The derivation assumes:
The electric field within the conductor is uniform.
All charge carriers have the same charge magnitude (e).
The mean drift velocity is constant along the wire.
The conductor is at steady state — no accumulation of charge at any point.
These assumptions make the relationship linear and idealised, but they hold well for ordinary metallic conductors under steady conditions.
Different materials vary mainly in number density (n) and mobility (μ) of charge carriers.
Metals: Very high n, meaning a given current requires only a tiny drift velocity.
Semiconductors: Much smaller n, so drift velocity must be higher for the same current.
Insulators: Extremely low n, so almost no measurable drift occurs.
Thus, while the equation I = A n e v holds universally, the numerical contribution from n determines how effectively each material can carry charge.
Practice Questions
Question 1 (2 marks)
A copper wire has a cross-sectional area of 1.2 × 10⁻⁶ m². The number density of free electrons in copper is 8.5 × 10²⁸ m⁻³, and the mean drift velocity of electrons is 4.0 × 10⁻⁴ m s⁻¹.
Calculate the current in the wire.
Mark scheme:
Substitution into I = A n e v correctly shown or implied (1 mark)
I = (1.2 × 10⁻⁶) × (8.5 × 10²⁸) × (1.6 × 10⁻¹⁹) × (4.0 × 10⁻⁴)Correct answer with appropriate unit: 6.5 A (accept 6.5 ± 0.1 A) (1 mark)
Question 2 (5 marks)
Explain, using the relationship I = A n e v, how the macroscopic current in a wire depends on the microscopic motion of charge carriers. Discuss what would happen to the drift velocity if the same current flowed through a wire of smaller cross-sectional area made from the same material.
Mark scheme:
States that current depends on the product of number density, charge per carrier, cross-sectional area, and mean drift velocity (1 mark)
Explains that microscopic motion (drift velocity of charge carriers) produces the macroscopic current (1 mark)
Recognises that for the same material, n and e are constant (1 mark)
Correctly deduces that if A decreases and I remains the same, v must increase (1 mark)
Provides a clear explanation relating the physical meaning — carriers move faster to maintain the same charge flow per second through a smaller area (1 mark)

