OCR Specification focus:
‘Understand units for I, A, n, e, and v; drift speeds are small despite large current.’
Understanding the units and typical magnitudes involved in electric current and charge carrier motion is fundamental to interpreting electrical phenomena. This subtopic connects the microscopic motion of individual charged particles to the macroscopic current observed in conductors.
The Importance of Units in Physics
In physics, units provide a standard for measuring quantities, ensuring results are meaningful and comparable. For the mean drift velocity equation I=AnevI = A n e vI=Anev, every variable represents a physical quantity with specific SI units. Precision in recognising and converting these units is vital for accurate analysis and communication of experimental results.
Electric Current (I)
Electric current is defined as the rate of flow of charge through a conductor.
Electric current (I): The rate of flow of electric charge past a given point in a circuit.
The SI unit of current is the ampere (A).
1 ampere = 1 coulomb of charge passing per second, or 1 A = 1 C s⁻¹.
Measurable using an ammeter, current is a macroscopic quantity, representing the cumulative effect of billions of moving charge carriers.
In typical household or laboratory circuits, currents range from a few milliamperes (mA) in delicate circuits to several amperes in high-power devices.
Cross-sectional Area (A)
The cross-sectional area of a conductor affects how much current can pass through it.
Cross-sectional area (A): The surface area through which charge carriers move, perpendicular to their direction of motion.
The SI unit is square metres (m²).
Conductors such as wires have small areas—often in the range of 10⁻⁶ to 10⁻⁴ m²—but these values are sufficient to support measurable current due to the enormous number of charge carriers.
The area determines the current density (J = I / A), which expresses how concentrated the current is within the conductor.
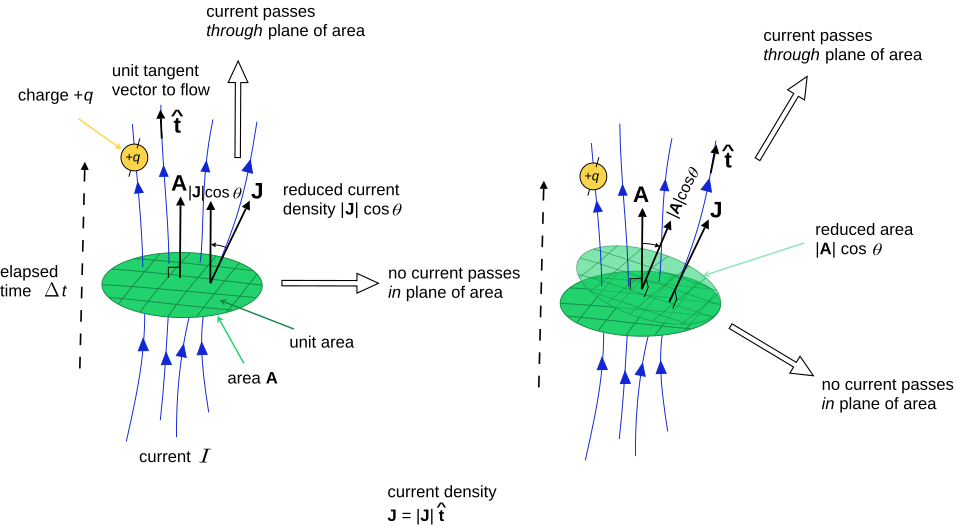
Diagram showing a conductor’s cross-section with labels for current I, elemental area dA, and current density J. It clarifies that J measures current per unit area (SI units A m⁻²). This directly supports the unit relationships used alongside I, A, and J. Source.
Number Density (n)
Number density describes the number of free charge carriers per unit volume in a material.
Number density (n): The number of free charge carriers (such as electrons) per cubic metre of material.
The SI unit is m⁻³.
For metals like copper, n ≈ 8.5 × 10²⁸ m⁻³, showing an extremely high density of mobile electrons.
Semiconductors have much smaller values, typically 10²²–10²⁵ m⁻³, and insulators have effectively zero free charge carriers under normal conditions.
The vast difference in n values explains why metals conduct so efficiently compared to semiconductors or insulators.
Elementary Charge (e)
The elementary charge is the smallest unit of electric charge that can exist independently.
Elementary charge (e): The magnitude of the charge on a single electron or proton, equal to 1.6 × 10⁻¹⁹ coulombs.
The charge of an electron is −e, while a proton carries +e.
All measurable charges are quantised, meaning they are integer multiples of e.
This fundamental constant is essential for linking the microscopic and macroscopic scales of current flow.
Mean Drift Velocity (v)
Mean drift velocity is the average velocity of charge carriers moving through a conductor under an electric field.
Mean drift velocity (v): The average velocity of charge carriers in a conductor due to an applied potential difference.
The SI unit is metres per second (m s⁻¹).
In metallic conductors, drift velocities are typically very small, often around 10⁻⁴ to 10⁻³ m s⁻¹, even when the current appears large.
This small speed arises because of the enormous number of charge carriers moving simultaneously, resulting in significant overall current despite slow individual motion.
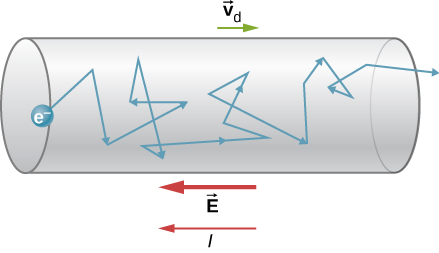
Sketch of an electron’s zig-zag path in a conductor with an indicated drift velocity vdv_dvd opposite to conventional current direction. It distinguishes rapid random motion from the much smaller average drift (units m s⁻¹). Extra label “electric field” may appear; this is acceptable context and within syllabus scope. Source.
The Continuity Equation
The mean drift velocity equation connects all these quantities and forms the foundation for understanding electrical conduction.
EQUATION
—-----------------------------------------------------------------
Mean Drift Velocity Equation: I = A n e v
I = Electric current (A)
A = Cross-sectional area of the conductor (m²)
n = Number density of charge carriers (m⁻³)
e = Elementary charge (C)
v = Mean drift velocity (m s⁻¹)
—-----------------------------------------------------------------
This relationship highlights that a large current can result from a high number density or a large cross-sectional area, even if the drift velocity remains small.
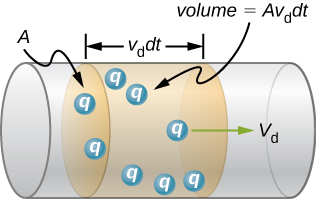
Schematic of a wire segment of length vddtv_d dtvddt and area A containing nAvddtnA v_d dtnAvddt charge carriers of charge q. It shows how charge in that segment gives I=nqAvdI = nqA v_dI=nqAvd (SI units: I in A, A in m², n in m⁻³, q in C, v_d in m s⁻¹). The figure uses standard labels and introduces no extra concepts. Source.
Typical Magnitudes in Context
To appreciate the scale of quantities involved, it is useful to consider approximate magnitudes encountered in typical situations:
Electric current (I): 10⁻³–10² A (from sensor circuits to household appliances)
Cross-sectional area (A): 10⁻⁶–10⁻⁴ m² (fine wire to thick cable)
Number density (n): 10²⁸ m⁻³ (typical metal conductor)
Elementary charge (e): 1.6 × 10⁻¹⁹ C (fundamental constant)
Mean drift velocity (v): 10⁻⁴–10⁻³ m s⁻¹ (slow motion of electrons)
Although individual electrons move slowly, the overall effect is rapid because electrical energy propagates at nearly the speed of light through the electric field in the conductor.
Relationships and Implications
The interplay between these quantities explains many practical aspects of circuits:
Increasing current (I) for a fixed wire requires higher drift velocity (v), more charge carriers (n), or a larger cross-sectional area (A).
For a given material, where n and e are constants, adjusting the area or voltage changes v, thus controlling current.
In semiconductors, small variations in n—achieved by doping—significantly affect current and conductivity.
Significance of Small Drift Velocities
Despite seemingly slow motion, electrons transfer energy extremely efficiently. The electric field applied across the conductor causes instantaneous acceleration and scattering, creating a steady average velocity that maintains current flow. The small magnitude of v ensures stability and prevents excessive heating, making steady conduction possible in everyday circuits.
FAQ
Electrons in a conductor move randomly at speeds around 10⁵–10⁶ m s⁻¹ due to thermal energy. However, these random motions cancel out overall, giving a very small net average velocity known as the mean drift velocity.
The drift velocity is determined by the applied electric field, which slightly biases the random motion of electrons in one direction, producing a net current even though individual electrons move much faster in random directions.
Yes. The mean drift velocity depends on the number density (n) of charge carriers in the material.
Metals with a high number density, such as copper or silver, require only a small drift velocity for a given current.
Metals with fewer free electrons per cubic metre need a higher drift velocity to achieve the same current.
Therefore, the same current in wires of different metals may correspond to very different electron drift speeds.
From the equation I = A n e v, if A decreases while I remains constant, the drift velocity v must increase proportionally.
This means electrons move faster on average through a narrower wire to maintain the same current.
However, increasing drift velocity also increases resistance slightly, as higher speeds mean more frequent collisions and greater heating effects within the conductor.
When a circuit is switched on, an electric field is established almost instantaneously throughout the conductor.
Although electrons move slowly, the field causes all free electrons in the wire to begin drifting almost at once.
The electrical energy is transferred via this field, so the observable effect—such as a lamp lighting—occurs almost immediately, despite the electrons’ small mean drift speed.
The equation I = A n e v involves quantities with very different orders of magnitude.
I in amperes (A)
A in square metres (m²)
n in per cubic metre (m⁻³)
e in coulombs (C)
v in metres per second (m s⁻¹)
Small errors in units—such as using millimetres instead of metres—can change results by factors of a million.
Using SI units ensures consistency and accuracy when comparing results or verifying physical relationships in experimental data.
Practice Questions
Question 1 (2 marks)
State the SI unit of mean drift velocity and explain why, in a metal conductor, the drift velocity of electrons is typically very small even when the current is large.
Mark scheme:
1 mark for correctly stating the SI unit of mean drift velocity as metres per second (m s⁻¹).
1 mark for explaining that drift velocity is small because the number density of charge carriers in a metal is very high, so a large current can flow even when each electron moves slowly.
Question 2 (5 marks)
A copper wire has a cross-sectional area of 1.0 × 10⁻⁶ m² and carries a steady current of 2.0 A. The number density of free electrons in copper is 8.5 × 10²⁸ m⁻³ and the elementary charge is 1.6 × 10⁻¹⁹ C.
(a) Using the equation I = A n e v, calculate the mean drift velocity of the electrons.
(b) Comment on the significance of your result with reference to the motion of electrons and the observable effect of electric current.
Mark scheme:
(a) Calculation (3 marks total):
1 mark for correctly rearranging the equation: v = I / (A n e).
1 mark for correct substitution: v = 2.0 / (1.0 × 10⁻⁶ × 8.5 × 10²⁸ × 1.6 × 10⁻¹⁹).
1 mark for correct numerical answer: v ≈ 1.5 × 10⁻⁴ m s⁻¹ (allow range 1.4–1.6 × 10⁻⁴ m s⁻¹).
(b) Explanation (2 marks total):
1 mark for recognising that the drift velocity is very small, indicating slow average motion of electrons.
1 mark for explaining that despite this small velocity, current appears to act instantly because the electric field propagates rapidly through the conductor, causing energy transfer at near light speed.

