OCR Specification focus:
‘n is high in metals, lower in semiconductors, and extremely low in insulators.’
The number density of charge carriers (n) determines how effectively materials conduct electric current. Comparing n across conductors, semiconductors, and insulators reveals why these materials behave so differently in electrical circuits and devices.
Understanding Number Density (n)
The number density, symbolised by n, represents the number of free charge carriers per unit volume within a material. It quantifies how many electrons or ions are available to move and therefore contribute to electric current when a potential difference is applied.
Number Density (n): The number of charge carriers (usually electrons in metals) per cubic metre of a material, determining its ability to conduct electric current.
Because current (I) is given by I = A n e v, where A is the cross-sectional area, e the elementary charge, and v the mean drift velocity, the value of n directly influences how much current flows for a given applied voltage.
Although the mean drift velocity of individual carriers is often very small, the large number of available carriers in good conductors allows a substantial total current.
Comparing n Across Materials
The OCR specification highlights that “n is high in metals, lower in semiconductors, and extremely low in insulators.”
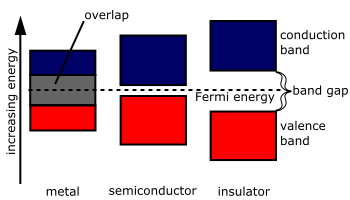
Schematic band diagrams comparing a metal (overlapping bands), a semiconductor (small band gap), and an insulator (large band gap). A small or zero gap means many carriers are available, corresponding to higher n; a large gap suppresses carriers, giving extremely low n. This figure focuses on the qualitative relationships needed at A-level. Source.
This distinction forms the basis for classifying materials by their electrical conductivity.
Metals: High Number Density
Metals are excellent electrical conductors because they contain a vast number of delocalised electrons that can move freely through the metallic lattice.
Each metal atom contributes at least one free electron to the conduction band.
Typical number densities for metals are around 10²⁸ to 10²⁹ electrons per cubic metre.
Common examples include copper, aluminium, and silver, where metallic bonding ensures a constant supply of free electrons.
The lattice structure provides a “sea” of electrons that can respond almost instantly to an electric field, leading to high conductivity.
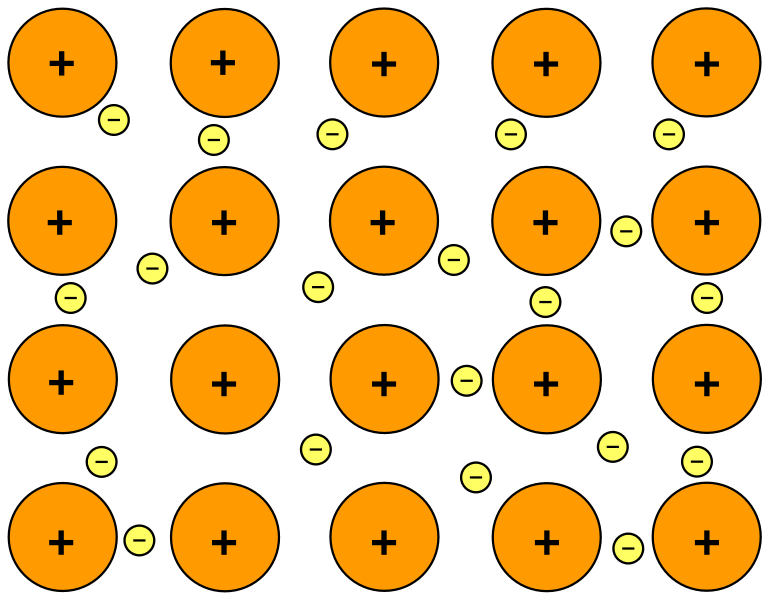
Diagram of metallic bonding showing positive ion cores in a lattice surrounded by a sea of delocalised electrons. The abundance of mobile electrons corresponds to a very large number density n, explaining why metals conduct so effectively. Extra atomic-structure details beyond the syllabus are minimised and purely illustrative. Source.
Because of this immense n, even though individual electrons drift slowly, the overall macroscopic current is large. The mean drift velocity v in metals is typically in the order of 10⁻⁴ m/s, yet current can reach several amperes due to the sheer quantity of electrons involved.
Semiconductors: Moderate Number Density
Semiconductors occupy a middle ground between metals and insulators. Their number density of charge carriers is much smaller than in metals, but it can vary depending on temperature or impurities (doping).
At low temperatures, pure or intrinsic semiconductors have very few free charge carriers, as electrons remain bound within the crystal lattice.
As temperature increases, some electrons gain enough energy to cross the band gap into the conduction band, leaving behind holes in the valence band. Both electrons and holes act as charge carriers.
The typical n value for intrinsic semiconductors such as silicon or germanium is around 10¹⁶ to 10²¹ m⁻³, which is millions of times lower than in metals.
Intrinsic Semiconductor: A pure semiconductor in which charge carriers are generated solely by thermal excitation across the band gap.
In practical applications, semiconductors are often doped to deliberately increase n. Adding small amounts of impurity atoms creates n-type or p-type materials with controlled numbers of electrons or holes.
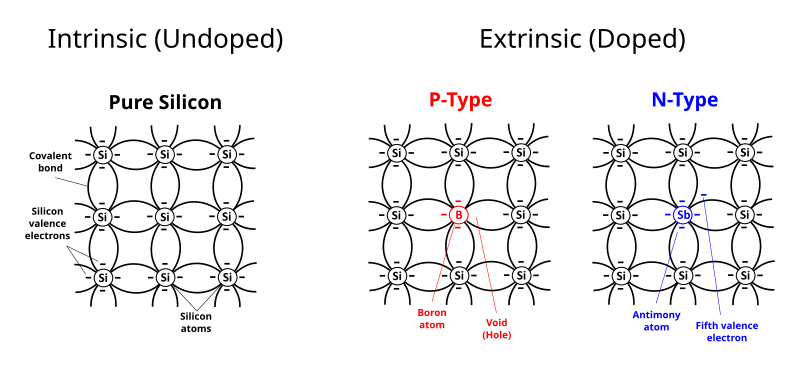
Labeled schematic of silicon doped n-type (extra electrons from donors) and p-type (holes from acceptors). Doping raises the number density n by creating additional carriers, enabling practical conduction in devices. The figure includes standard symbols for donors/acceptors consistent with A-level presentation. Source.
n-type semiconductors contain extra electrons (donor impurities).
p-type semiconductors contain additional holes (acceptor impurities).
After doping, the number density can increase by several orders of magnitude—up to around 10²² to 10²⁴ m⁻³—making them suitable for use in diodes, transistors, and integrated circuits.
EQUATION
—-----------------------------------------------------------------
Electric Current (I) = A n e v
I = Current (A)
A = Cross-sectional area (m²)
n = Number density of charge carriers (m⁻³)
e = Elementary charge (1.6 × 10⁻¹⁹ C)
v = Mean drift velocity (m/s)
—-----------------------------------------------------------------
Even with a smaller n than metals, semiconductors can still carry appreciable current when external energy (from heat, light, or voltage) promotes additional carriers.
Insulators: Extremely Low Number Density
Insulators have an extremely small number density of charge carriers, meaning very few electrons are free to move.
In an insulator, almost all electrons are tightly bound within filled valence bands, with a large band gap (often >5 eV) to the conduction band.
As a result, almost no electrons can gain sufficient energy to move into the conduction band at ordinary temperatures.
Typical n values for insulators are between 10⁵ and 10¹⁰ m⁻³, making them billions of times lower than those in metals.
Insulator: A material with a negligible number of free charge carriers due to a large energy band gap, preventing significant current flow under normal conditions.
Examples include rubber, glass, ceramics, and plastic. In these materials, the applied voltage produces almost no drift of electrons, leading to very high resistivity.
However, when subjected to extremely high voltages or temperatures, even insulators may experience dielectric breakdown, where bound electrons are liberated, temporarily increasing n and allowing current to flow destructively.
Significance of Comparing n
Understanding how n varies among materials allows physicists and engineers to predict and manipulate conductivity, resistivity, and current flow.
High n (metals): Excellent conductors for power transmission and circuitry.
Moderate n (semiconductors): Tunable conduction properties for logic devices and sensors.
Very low n (insulators): Essential for insulation, preventing unwanted current leakage.
The difference in n also influences thermal properties, carrier mobility, and energy efficiency in electrical systems. Therefore, comparing number densities across materials provides foundational insight into how all electrical devices—from wires to microchips—operate at the microscopic level.
FAQ
The number density in a metal depends on the number of free electrons contributed by each atom and the material’s atomic structure.
Each metal atom typically donates one or more electrons to the conduction band. For example:
Copper contributes one electron per atom.
Aluminium contributes three electrons per atom.
The overall n is calculated by multiplying the number of conduction electrons per atom by the atomic number density (atoms per cubic metre). Metals with closely packed lattices and multiple conduction electrons per atom therefore have higher n values.
Doping introduces impurity atoms that either donate or accept electrons, drastically increasing the number of charge carriers.
n-type doping adds donor atoms (e.g. phosphorus in silicon), contributing extra electrons to the conduction band.
p-type doping adds acceptor atoms (e.g. boron in silicon), creating holes in the valence band.
Even a tiny fraction of impurity atoms (one in ten million) can increase n by several orders of magnitude because each dopant atom introduces a free carrier into the material.
In semiconductors, rising temperature provides energy for more electrons to cross the band gap into the conduction band.
As temperature increases:
The number of electrons in the conduction band rises.
A corresponding number of holes appear in the valence band.
n therefore increases rapidly with temperature.
This thermal excitation effect continues until the semiconductor behaves almost like a poor metal at high temperatures. In contrast, metals show little change in n with temperature because their carrier density is already very high.
Under extreme conditions, such as high electric fields or temperatures, insulators can undergo dielectric breakdown or thermal excitation.
Strong electric fields can supply enough energy to free bound electrons, creating temporary charge carriers.
High temperatures can excite some electrons across the large band gap.
Both effects raise n slightly, allowing small currents to flow. However, this is often destructive and irreversible because the material structure can be damaged once breakdown occurs.
No. While n is crucial, mobility (μ)—how easily carriers move through the material—also plays a key role.
Electrical conductivity (σ) depends on both:
σ = n e μ, where e is the elementary charge.
A material with a high n but low mobility (due to scattering or impurities) may conduct less effectively than one with slightly lower n but higher mobility. Therefore, both the availability of carriers and their freedom to move determine overall conductivity.
Practice Questions
Question 1 (2 marks)
Explain why the number density of charge carriers (n) is much higher in metals than in semiconductors.
Mark Scheme:
1 mark for stating that metals have a large number of delocalised or free electrons available for conduction.
1 mark for explaining that semiconductors have far fewer charge carriers because most electrons are bound within the crystal lattice (or due to the presence of a band gap restricting carrier movement).
Question 2 (5 marks)
Compare and contrast the number density of charge carriers (n) in metals, semiconductors, and insulators, and explain how this affects their electrical conductivity. Include in your answer the approximate order of magnitude of n for each material type.
Mark Scheme:
1 mark for stating that metals have a very high number density (around 10²⁸ to 10²⁹ m⁻³).
1 mark for stating that semiconductors have a much lower number density (around 10¹⁶ to 10²¹ m⁻³), which increases with temperature or doping.
1 mark for stating that insulators have an extremely low number density (around 10⁵ to 10¹⁰ m⁻³).
1 mark for correctly linking higher n to greater electrical conductivity and lower n to poor conductivity.
1 mark for an overall comparative statement demonstrating understanding, e.g. "Metals conduct well due to many free electrons, semiconductors conduct moderately and variably, while insulators conduct very poorly due to almost no free carriers."

