AP Syllabus focus:
‘Introduction to the basic terminology of statistical studies, distinguishing between a population (all subjects of interest) and a sample (a subset of the population chosen for study). Emphasize the critical role of defining these terms precisely to ensure the validity and reliability of study findings.’
This section explores how clearly defining populations and samples forms the basis of every statistical study, ensuring researchers draw reliable, meaningful conclusions from carefully gathered data.
Defining the Foundations of Statistical Studies
Understanding the difference between a population and a sample is essential because every statistical investigation relies on these two core ideas. In statistics, researchers often face practical limits—time, money, or access—that prevent them from measuring every individual of interest. As a result, they draw conclusions about a larger group by examining a smaller, carefully chosen subset.
Population: The entire group of individuals or objects that a researcher wants to study or understand.
A population is defined before any data collection begins, and this clear definition ensures that the scope of the research is unambiguous. Because populations can be extremely large—such as all high school students in the United States—researchers typically need a more manageable approach.
After identifying the population, researchers collect data from a subset of it.
Sample: A smaller group selected from the population to represent it in a statistical study.
Between these two ideas lies the central challenge of statistical work: ensuring the sample is representative enough for findings to reflect the truth about the larger population.
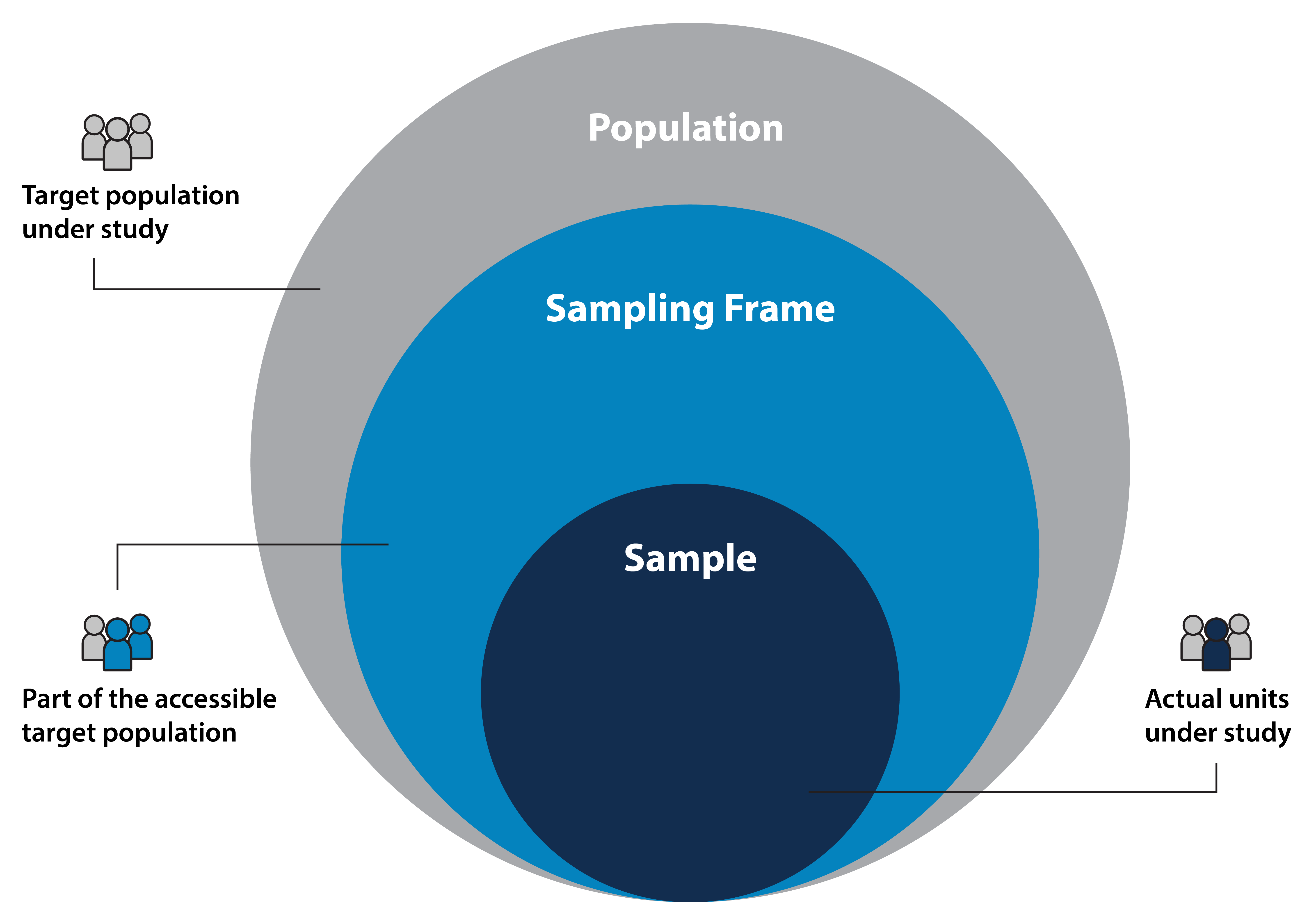
This diagram shows the relationship between a population, an accessible sampling frame, and the final selected sample, illustrating how samples are subsets of broader groups. Source.
When a sampling frame is incomplete or inaccurate, the sample may fail to reflect the true population.
Importance of Clear Definitions
A study must explicitly identify its population of interest before selecting a sample. Without a precise definition, any conclusions drawn may not apply to the intended group. For example, a study investigating the eating habits of “teenagers” must specify whether this means ages 13–19, high school students only, or some other subgroup. Precision shapes the validity and interpretability of all results.
Equally important is defining the sampling frame, the list or method used to identify members who could be selected. When a sampling frame is incomplete or inaccurate, the sample may fail to reflect the true population.
Why Sampling Is Necessary
Because studying an entire population is often impossible, samples provide a practical alternative. Well-chosen samples allow researchers to:
Make inferences about the population efficiently.
Reduce the cost and time of data collection.
Conduct studies that would otherwise be unmanageable or unethical.
Use random selection to minimize biases and support valid conclusions.
A carefully collected sample serves as a microcosm of the population—mirroring its key characteristics as closely as possible.
Representativeness and Reliability
A major goal in sampling is obtaining a group that accurately reflects population traits. A representative sample reduces the risk of systematic error and increases confidence that patterns observed in the data truly apply to the population.
Representativeness: The degree to which a sample reflects the characteristics and diversity of its population.
Researchers must be aware that even well-designed samples vary naturally. This natural fluctuation is known as sampling variability, and it is expected whenever chance plays a role in selection. Recognizing variability helps researchers interpret results with appropriate caution and avoid overstating the certainty of their findings.
The Role of Random Selection
Random selection is a cornerstone of trustworthy sampling. When every individual in the population has an equal chance of being chosen, researchers reduce the likelihood of selection bias, a systematic distortion that leads to misleading results.
Random selection helps ensure:
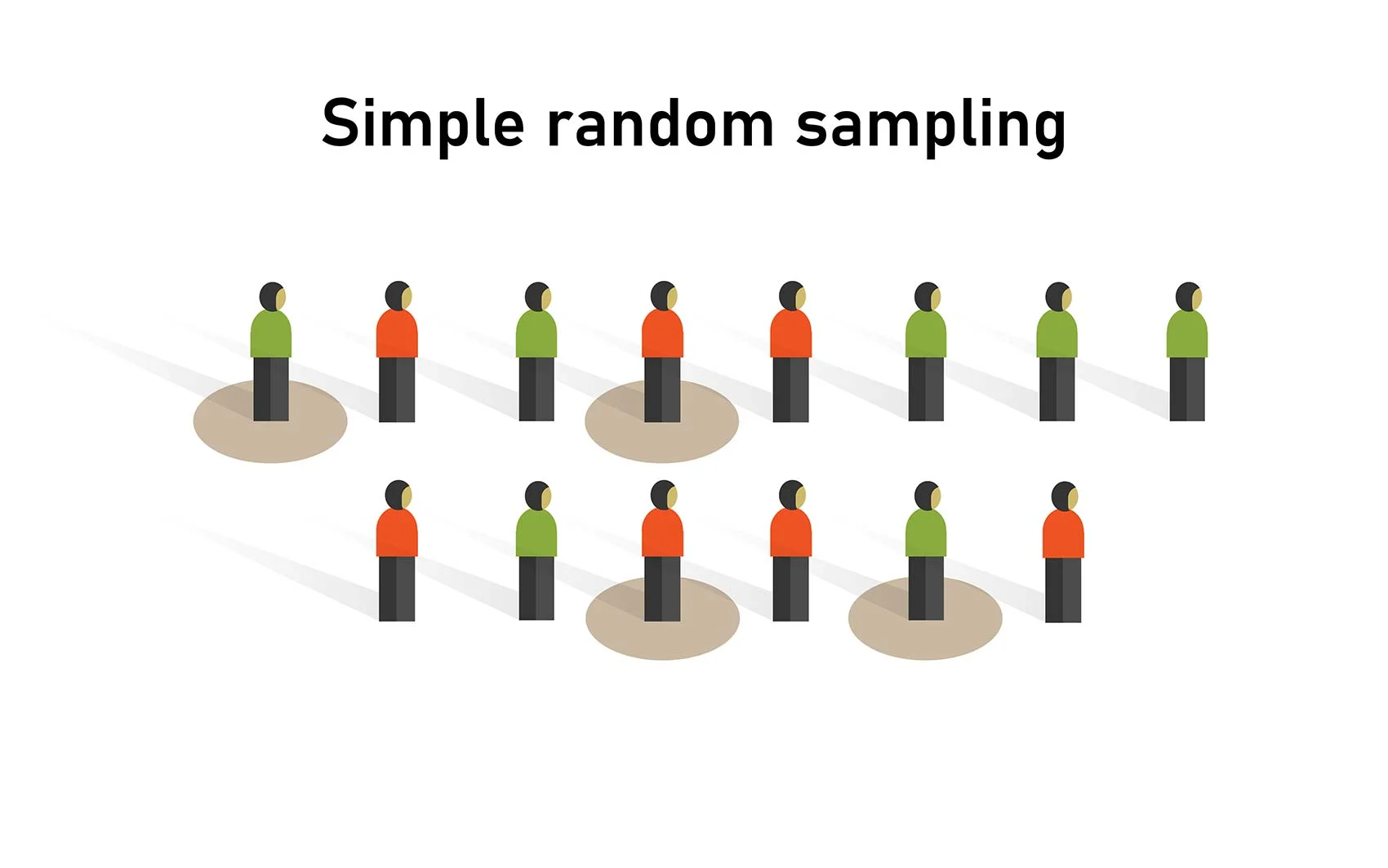
This visual demonstrates simple random sampling, where each individual has an equal chance of selection, reinforcing the role of randomness in reducing bias. Source.
Fair representation of subgroups.
Reduced influence of personal judgment or convenience.
Increased credibility of the study’s claims.
A sound basis for applying probability to make inferences.
Without randomness, a study’s conclusions may not reflect the population accurately, even if the sample is large.
How Populations and Samples Support Valid Study Findings
By clearly defining populations and selecting appropriate samples, researchers lay the groundwork for reliable statistical inference. The structure provided by these definitions ensures that:
Data are collected from individuals who genuinely represent the broader group.
The study's goals align with its methods.
Findings can be interpreted in context without overgeneralization.
The logical link between sample results and population truths remains intact.
In AP Statistics, understanding populations and samples extends beyond memorizing definitions. It involves recognizing how carefully choosing and defining each contributes to the validity and reliability of every statistical conclusion.
FAQ
The target population refers to the full group a researcher ultimately wishes to draw conclusions about, while the accessible population includes only the individuals that can realistically be reached for sampling.
The accessible population is almost always smaller, and differences between the two can limit how broadly results may be applied.
Representativeness improves when the sample mirrors the population’s diversity in key characteristics, such as age, location, or experience.
It becomes weaker when:
Certain groups are missing from the sampling frame
Participation rates differ between subgroups
The sample is too small to capture natural variation
A sampling frame becomes inaccurate when people move, new members join the population, or old listings become irrelevant.
Outdated sampling frames increase the risk of excluding parts of the population, which can lead to bias and reduce confidence in conclusions drawn from the sample.
Larger samples generally reduce sampling variability, but only when the sample is selected using appropriate random methods.
If selection is biased, increasing the sample size does not improve representativeness; it may simply reinforce the bias by gathering more data from the wrong individuals.
Researchers often specify inclusion and exclusion criteria that determine exactly who belongs in the population.
They may also:
Clarify time periods (e.g., residents in the past 12 months)
Define relevant characteristics (e.g., adults aged 18+ in a district)
Align population definitions with the study’s objectives to avoid ambiguity
Practice Questions
Question 2 (4–6 marks)
A local council wants to understand public opinion on plans to redesign a community park. The council defines the population as “all residents living within the council boundary”. They obtain a list of households from the most recent census and randomly select 500 households to contact.
(a) Explain why the list of households is considered a sampling frame.
(b) Describe one potential problem with using this sampling frame for selecting residents.
(c) The council claims the sample will allow them to make inferences about the entire population. State one condition that must be met for this inference to be valid, and explain why.
Question 2 (4–6 marks)
(a) 1 mark
States that the list of households acts as the sampling frame because it is the list from which the sample is drawn or identifies members of the population available for selection.
(b) 1–2 marks
1 mark for identifying a relevant issue (e.g., outdated census data, missing households, excluding people without fixed addresses).
1 additional mark for explaining how this issue affects representativeness or leads to potential bias.
(c) 2–3 marks
1 mark for stating that the sample must be representative or that random selection must be properly implemented.
1–2 marks for explaining why this condition is necessary (e.g., ensures every resident has a chance of being included, supports valid inference, reduces bias, allows generalisation).
Question 1 (1–3 marks)
A researcher wants to study the sleeping habits of all students at a large secondary school.
(a) Identify the population of interest.
(b) The researcher selects 60 students at random from the school register. What is the term used to describe this smaller group?
(c) Explain why clearly defining the population is important in this study.
Question 1 (1–3 marks)
(a) 1 mark
Correctly identifies the population as all students at the secondary school.
(b) 1 mark
States that the 60 selected students form the sample.
(c) 1 mark
Provides a clear explanation that defining the population ensures the findings apply to the intended group, avoids ambiguity, or supports valid generalisation.

