Chemical kinetics examines how fast reactions occur, why rates vary, and how experimental data reveals relationships between reactant concentrations and reaction speed.

Rate of Reaction

The rate of reaction describes how quickly reactants are converted into products. It is a central concept in kinetics and underpins all rate equations and graphical analyses.

In practice, rates can be expressed as the decrease in concentration of a reactant or the increase in concentration of a product. The sign is usually ignored, as rate refers to speed rather than direction.

Rates are affected by several factors, including concentration, temperature, pressure (for gases), surface area, and catalysts. This subtopic focuses specifically on how concentration affects rate.

Rate Equations

A rate equation (also called a rate law) shows how the rate depends on the concentrations of reactants involved in the slow, rate-determining step of a reaction.

The overall structure of a rate equation must be deduced from experimental data and cannot usually be obtained directly from a balanced chemical equation.

Order of Reaction

The order of reaction indicates how the rate depends on the concentration of a particular reactant.

Orders can be zero, first, second, or fractional, although OCR A-Level Chemistry focuses on zero, first, and second order reactions.

Zero Order

• Rate is independent of reactant concentration

• Changing concentration has no effect on rate

• Common in reactions involving catalysts or saturated surfaces

In zero-order kinetics, the rate is constant and does not change as the reactant concentration falls.

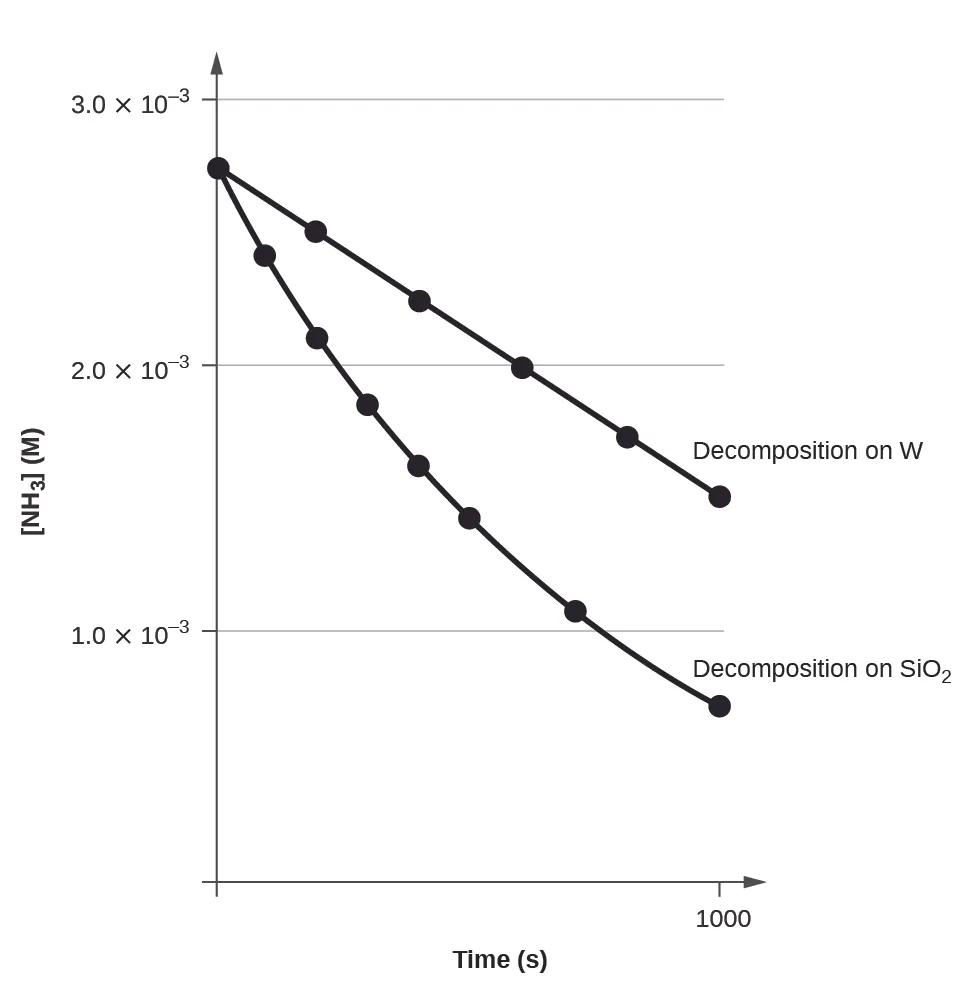
This graph compares zero-order and first-order concentration–time behaviour, showing constant-rate linear decrease versus exponential decay. The surface chemistry context is extra detail, but the order comparison directly supports understanding of reaction order. Source

Mathematically, the concentration term does not appear in the rate equation.

First Order

• Rate is directly proportional to concentration

• Doubling concentration doubles the rate

• Many decomposition and radioactive decay processes follow first order kinetics

First order reactions are especially important because they exhibit a constant half-life.

Second Order

• Rate depends on the square of one reactant concentration, or the product of two reactant concentrations

• Doubling concentration increases rate by a factor of four

Overall Order

The overall order of reaction is found by adding together the individual orders of all reactants in the rate equation.

For example, if rate = k[A]¹[B]², the overall order is three. The overall order gives insight into the complexity of the rate-determining step but does not necessarily match the stoichiometry of the equation.

Rate Constant, k

The rate constant links the rate of reaction to reactant concentrations and is specific to a particular reaction at a fixed temperature.

The units of k vary depending on the overall order of the reaction. For example:

• Zero order: mol dm⁻³ s⁻¹

• First order: s⁻¹

• Second order: dm³ mol⁻¹ s⁻¹

Although concentration affects rate, it does not change the value of k. Temperature changes, however, do alter k significantly.

Half-life

The half-life of a reaction is particularly important for first order processes.

The beakers illustrate concentration halving at equal time intervals, a defining feature of first-order half-life behaviour. Colour is used purely as a visual aid and is not chemically significant. Source

For first order reactions, the half-life is constant and independent of the initial concentration. This property is used experimentally to identify first order kinetics. For zero and second order reactions, the half-life changes as the reaction proceeds.

Deducing Orders from Experimental Data

Orders of reaction must be deduced experimentally, commonly by comparing how rate changes when concentration is varied.

Reaction orders are found experimentally by measuring how the rate changes when reactant concentrations are changed.

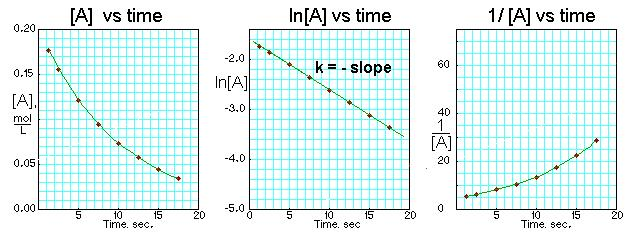
These plots show how first-order data produce a straight line when ln[A] is plotted against time. The use of integrated-rate-law graphs extends beyond this subsubtopic but reinforces what first-order behaviour looks like experimentally. Source

Key principles used include:

• If doubling concentration doubles rate → first order

• If doubling concentration quadruples rate → second order

• If changing concentration has no effect → zero order

Only one reactant concentration is changed at a time, while others are kept constant, allowing the effect of each reactant to be isolated.

Writing Rate Equations

Once the orders are known, the rate equation can be written by:

• Including only reactants that affect the rate

• Raising each concentration term to its experimentally determined order

• Combining all terms with the rate constant, k

The resulting equation summarises the kinetic behaviour of the reaction and forms the basis for further analysis in graphical and mechanistic studies later in the course.