OCR Specification focus:
‘Explain temperature effects on rate and k; use k = Ae^(−Ea/RT) and ln k = −Ea/RT + ln A to find Ea.’
Reaction rates increase with temperature due to molecular energy changes. The Arrhenius equation quantitatively links temperature, activation energy and rate constant for chemical reactions.
Temperature and Reaction Rate
Increasing temperature generally increases the rate of a chemical reaction. This effect is explained by changes in the kinetic energy of particles and the frequency of successful collisions.
As temperature rises:
Particles move faster, increasing collision frequency
A greater proportion of particles possess energy equal to or greater than the activation energy
The number of successful collisions per second increases
It is important to note that temperature does not change the reaction mechanism. Instead, it affects how many reacting particles can overcome the activation energy barrier.
Activation Energy and Energy Distribution
Activation energy is the minimum energy required for reacting particles to collide successfully and form products.
Activation energy: The minimum energy that colliding particles must possess for a reaction to occur.
At any given temperature, particles have a range of energies described by a Maxwell–Boltzmann distribution. Only particles with energies equal to or above the activation energy contribute to reaction rate.
When temperature increases:
The distribution curve flattens and shifts to higher energies
The area under the curve beyond the activation energy increases
This increase explains the rapid rise in reaction rate with temperature
As temperature increases, the Maxwell–Boltzmann distribution becomes broader and shifts to higher energies, so a larger fraction of molecules have energy equal to or greater than Eₐ.
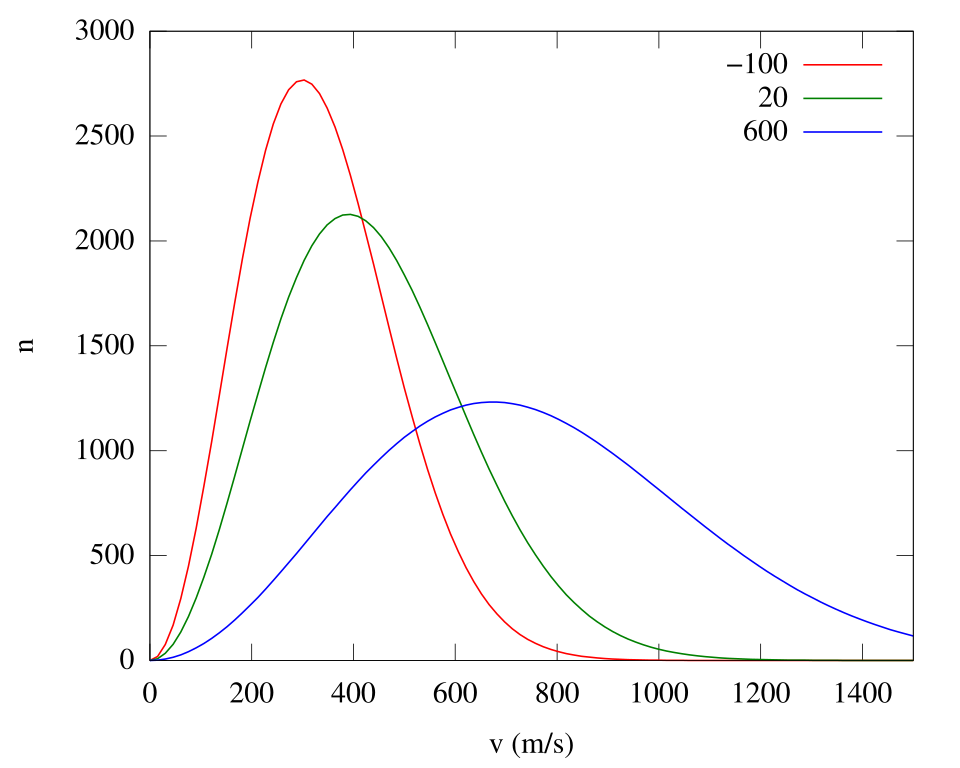
This Maxwell–Boltzmann plot shows how the distribution shifts and broadens at higher temperatures, increasing the proportion of fast (high-energy) particles. Although the x-axis shows speed rather than energy and Eₐ is not marked, it still illustrates the temperature-driven increase in the high-energy tail that explains faster reaction rates. Source
Even small temperature increases can significantly increase rate because the proportion of particles exceeding the activation energy rises sharply.
Rate Constant and Temperature Dependence
The rate constant (k) is a proportionality constant in the rate equation that depends on temperature.
Rate constant: A constant that relates reaction rate to reactant concentrations at a fixed temperature.
For a given reaction:
Increasing temperature increases k
Concentration, pressure, and catalysts do not affect k
A higher value of k corresponds to a faster reaction
The quantitative relationship between k, temperature, and activation energy is described by the Arrhenius equation.
The Arrhenius Equation
The Arrhenius equation provides a mathematical relationship between the rate constant and temperature.
Arrhenius equation (k) = Ae^(−Ea/RT)
k = rate constant
A = frequency factor (s⁻¹ for first-order reactions)
Ea = activation energy (J mol⁻¹)
R = gas constant (8.31 J mol⁻¹ K⁻¹)
T = temperature in kelvin (K)
This equation shows that:
k increases exponentially with temperature
A higher Ea makes the reaction more temperature-sensitive
The exponential term explains why temperature changes have a large effect on rate
The frequency factor A represents the frequency of correctly oriented collisions and is related to reaction geometry and mechanism.
Linear Form of the Arrhenius Equation
To allow experimental determination of activation energy, the Arrhenius equation can be rearranged into a linear form.
Linear Arrhenius equation (ln k) = −Ea/RT + ln A
ln k = natural logarithm of the rate constant
Ea = activation energy (J mol⁻¹)
R = gas constant (8.31 J mol⁻¹ K⁻¹)
T = temperature in kelvin (K)
A = frequency factor
This equation is in the form y = mx + c, where:
y = ln k
x = 1/T
Gradient = −Ea/R
Intercept = ln A
Rearranging the Arrhenius equation gives ln k = −Eₐ/RT + ln A, so plotting ln k against 1/T produces a straight line.
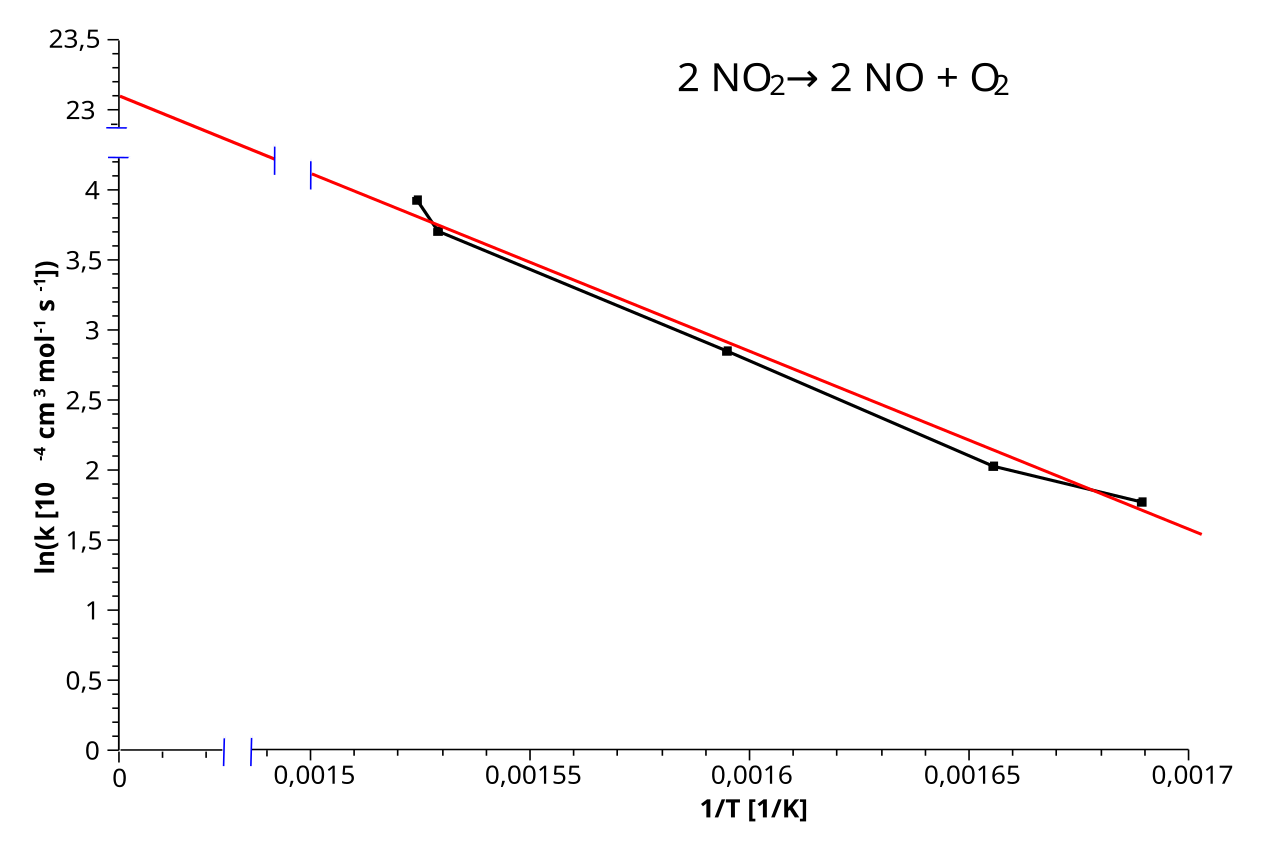
An Arrhenius plot graphs ln k against 1/T, producing a straight line for reactions that obey the Arrhenius equation. The gradient is equal to −Eₐ/R and can be used to determine activation energy, while the intercept corresponds to ln A. Source
A plot of ln k against 1/T produces a straight line. The gradient can be used to determine the activation energy.
Activation Energy from Experimental Data
Experimental rate constants measured at different temperatures can be used to calculate activation energy.
Key points when using Arrhenius data:
Temperature must always be in kelvin
The gradient of an ln k vs 1/T graph is negative
Activation energy is typically expressed in kJ mol⁻¹, but must be calculated in J mol⁻¹
A larger activation energy indicates a reaction that is slower at low temperatures and more sensitive to temperature changes.
Comparing Reactions Using Activation Energy
Activation energy values allow comparison of how readily different reactions occur.
Lower Ea → faster reaction at a given temperature
Higher Ea → slower reaction and stronger temperature dependence
Reactions with similar mechanisms often have similar A values but different Ea
Catalysts lower activation energy by providing an alternative reaction pathway. This increases rate without changing the position of equilibrium.
Common Misconceptions to Avoid
Temperature does not increase the energy of all particles equally
Activation energy is not reduced by temperature
The Arrhenius equation applies to the rate constant, not directly to rate
Doubling temperature does not double reaction rate
Understanding these distinctions is essential for correct application of the Arrhenius equation in OCR A-Level Chemistry.
FAQ
A small temperature rise significantly increases the number of particles in the high-energy tail of the energy distribution.
Because the Arrhenius equation contains an exponential term, even a modest increase in temperature produces a disproportionately large increase in the rate constant, k.
This effect is more pronounced for reactions with higher activation energies.
The frequency factor represents how often reactant particles collide with the correct orientation to react.
It depends on:
The complexity of the reaction
The orientation requirements of reacting molecules
The frequency of collisions
For simple reactions, A is often large; for complex reactions, A is smaller due to stricter orientation requirements.
Kelvin is an absolute temperature scale that reflects the true kinetic energy of particles.
Using degrees Celsius would distort the exponential relationship in the Arrhenius equation and produce incorrect values for the rate constant or activation energy.
All Arrhenius calculations therefore require temperature in kelvin.
In an Arrhenius plot, ln k is plotted against 1/T.
As temperature increases, 1/T decreases while ln k increases. This inverse relationship produces a straight line with a negative gradient.
The negative gradient directly reflects the −Ea/RT term in the Arrhenius equation.
Reactions with higher activation energies show greater sensitivity to temperature changes.
A small temperature increase produces a larger proportional increase in k for high-Ea reactions than for low-Ea reactions.
This is why some reactions appear almost unreactive at low temperatures but proceed rapidly when heated.
Practice Questions
Explain why increasing the temperature increases the rate constant, k, for a chemical reaction.
(2 marks)
Award one mark for each correct point:
Increasing temperature increases the proportion of particles with energy equal to or greater than the activation energy. (1 mark)
More successful collisions occur per second, so the value of the rate constant, k, increases. (1 mark)
The rate constant for a reaction was measured at several different temperatures.
a) State the Arrhenius equation and identify two variables that affect the value of the rate constant. (2 marks)
b) Explain how a graph of ln k against 1/T can be used to determine the activation energy for this reaction. (3 marks)
(5 marks)
a) (2 marks)
Award one mark for each correct point:
Correct statement of the Arrhenius equation: k = Ae^(−Ea/RT). (1 mark)
Identification of any two relevant variables that affect k, such as activation energy (Ea), temperature (T), or frequency factor (A). (1 mark)
b) (3 marks)
Award marks as follows:
A plot of ln k against 1/T gives a straight line. (1 mark)
The gradient of the line is equal to −Ea/R. (1 mark)
Activation energy can be calculated from the gradient by multiplying by −R. (1 mark)
Maximum 5 marks.

