Light travelling between different media can undergo bending or complete reflection depending on its incident angle. Understanding critical angle and total internal reflection is essential in optical physics.

1. Refraction and Boundary Behaviour

When a light ray passes between two transparent media of different optical densities, its speed changes, resulting in refraction — the bending of the ray at the interface.

As light enters a denser medium (higher refractive index), it slows down and bends towards the normal; when it exits into a less dense medium, it speeds up and bends away from the normal.

This change of direction depends on the angle of incidence and the refractive indices of the two materials, described mathematically by Snell’s Law.

EQUATION
—-----------------------------------------------------------------
Snell’s Law (Refractive indices and angles) = n₁ sin i = n₂ sin r
n₁ = Refractive index of first medium (no unit)
n₂ = Refractive index of second medium (no unit)
i = Angle of incidence (degrees or radians)
r = Angle of refraction (degrees or radians)
—-----------------------------------------------------------------

Only when light travels from a more optically dense medium to a less dense one (for example, glass to air) can total internal reflection (TIR) occur.

2. The Concept of the Critical Angle

As the angle of incidence increases, the refracted ray moves progressively further from the normal. At a specific incident angle, the refracted ray just grazes along the boundary, emerging at 90° to the normal. This angle is known as the critical angle.

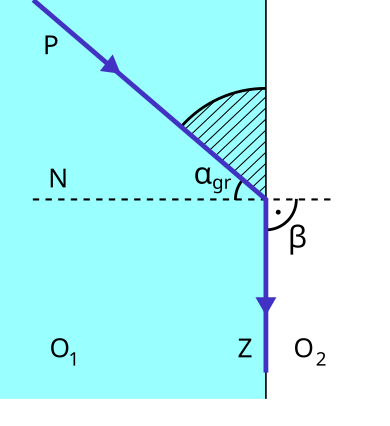
A labelled diagram showing refraction below the critical angle, the critical angle case with the refracted ray along the boundary, and total internal reflection for larger incidence angles. The normal and angles are clearly marked to reinforce sin C = 1/n. The layout is intentionally simple and uncluttered for A-level study. Source.

At this point, light is refracted along the boundary surface and any further increase in the angle of incidence causes total internal reflection, where the light is completely reflected within the denser medium.

EQUATION
—-----------------------------------------------------------------
Critical Angle Formula (for light passing from denser to rarer medium):
sin C = 1/n
C = Critical angle (degrees or radians)
n = Refractive index of the denser medium relative to the rarer medium (no unit)
—-----------------------------------------------------------------

This relationship is derived from Snell’s Law when the refracted ray’s angle equals 90°.

3. Conditions for Total Internal Reflection

For total internal reflection to occur, two essential conditions must be met:

• The light must travel from a more optically dense to a less optically dense medium.

  • Example: from glass (n ≈ 1.5) to air (n ≈ 1.0).

• The angle of incidence must be greater than the critical angle (C).

When these criteria are satisfied, no refracted ray emerges. Instead, all the light energy is reflected internally, obeying the law of reflection — the angle of incidence equals the angle of reflection.

The reflected ray remains within the denser medium, meaning energy is not transmitted into the second medium. TIR thus represents a perfect reflection process without energy loss due to transmission.

4. Understanding Through Wavefronts and Energy

At the critical angle, wavefronts at the boundary travel parallel to the interface. When the angle increases beyond this, the refracted component cannot propagate into the second medium — instead, an evanescent wave forms that decays exponentially with distance from the surface, carrying no net energy across the boundary.

This physical description explains why TIR results in a perfectly reflected wave within the denser medium.

5. Applications of Total Internal Reflection

The phenomenon of total internal reflection is used extensively in optical technologies because it allows efficient light transmission without energy loss.

Optical Fibres

• Structure: Very thin glass or plastic fibres with a core of higher refractive index surrounded by a cladding of lower refractive index.

• Operation: Light signals entering the core at small incident angles strike the core–cladding boundary above the critical angle, undergoing repeated total internal reflections.

• Benefit: This enables light to travel long distances with minimal signal loss, forming the basis for fibre-optic communication in telecommunications and medical imaging (endoscopes).

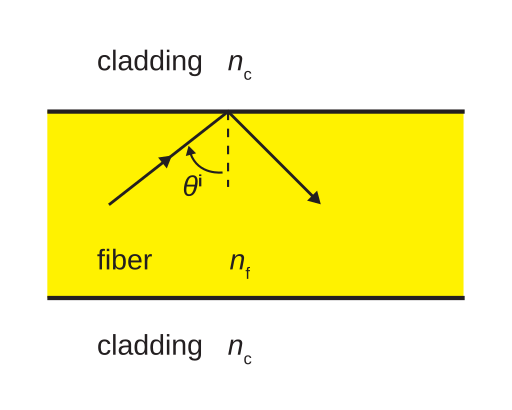
Schematic of an optical fibre with core and cladding, illustrating repeated total internal reflections when the incidence exceeds the critical angle. Arrows show propagation confined to the core. Extra labels (e.g., numerical aperture) are not shown here, keeping the focus on TIR. Source.

Prisms and Reflectors

• Right-angle prisms are used in cameras, binoculars, and periscopes.

• By arranging the prism so that light strikes a face at greater than the critical angle, internal reflection occurs, providing an efficient, high-quality reflection.

• Unlike ordinary mirrors, prisms using TIR do not rely on metallic coatings and therefore avoid light loss and surface degradation.

Diamond Sparkle

• Diamonds have a high refractive index (≈ 2.4), leading to a very small critical angle (~24°).

• Light entering a diamond is repeatedly internally reflected, greatly increasing the path length within the stone and producing intense sparkle — a direct consequence of multiple TIR events.

6. Relationship Between Refractive Index and Critical Angle

The refractive index of a medium quantifies how much light slows relative to its speed in a vacuum. From the critical angle equation, a higher n corresponds to a smaller C.

EQUATION
—-----------------------------------------------------------------
Refractive Index Relation (light in vacuum and medium):
n = c/v
n = Refractive index (no unit)
c = Speed of light in vacuum (3.00 × 10⁸ m s⁻¹)
v = Speed of light in the medium (m s⁻¹)
—-----------------------------------------------------------------

Thus, substances like glass (n ≈ 1.5) and diamond (n ≈ 2.4) exhibit smaller critical angles than water (n ≈ 1.33). This difference determines whether TIR can be used effectively for optical applications.

7. Experimental Observation of Critical Angle and TIR

Students can observe total internal reflection using a semicircular glass block and a ray box:

• A single light ray enters the flat face at varying incident angles.

• The emerging ray from the curved surface demonstrates refraction up to the critical angle, beyond which the ray no longer exits.

• Increasing the incident angle further shows the internally reflected ray, illustrating the condition for total internal reflection.

Careful measurement of the critical angle enables calculation of the refractive index using sin C = 1/n, validating the theoretical model described in the OCR specification.