The significance level α is a foundational idea in statistical inference, guiding the decision to reject or not reject a null hypothesis by setting an acceptable probability of error.

Understanding the Role of the Significance Level (α)

The significance level α establishes the boundary for deciding when sample evidence is strong enough to challenge the null hypothesis. The null hypothesis is the default assumption that a population parameter, such as a proportion, equals a specific value. Because statistical decisions are made under uncertainty, α formalizes the amount of risk a researcher is willing to accept when making an evidence-based decision.

The Purpose of α in Statistical Testing

Choosing α involves balancing caution and sensitivity. A smaller α reduces the chance of making an incorrect rejection of the null hypothesis, while a larger α increases the likelihood of detecting meaningful effects. This balance underscores why α is determined before analyzing data, ensuring that decision rules remain objective and unbiased.

What α Represents in Probabilistic Terms

The value of α is the probability of committing a specific type of inferential error—rejecting the null hypothesis when it is actually true. This is known as a Type I error.

Researchers accept α as the maximum tolerable probability of this error. Commonly used values such as 0.05 or 0.01 reflect conventional levels of tolerance for risk across fields that use significance testing.

After α is set, the testing framework uses sample data to determine whether the observed result is sufficiently unlikely under the assumption that the null hypothesis is true. This connection makes α a pivotal component in the overall logic of hypothesis testing.

α as a Decision Threshold

When conducting a significance test, the p-value—the probability, assuming the null hypothesis is true, of observing a test statistic as extreme as or more extreme than the value calculated from the sample—is compared directly to α. This comparison forms the basis of the formal decision rule used in hypothesis testing.

If the p-value is less than or equal to α, the data are considered inconsistent with the null hypothesis, and the null hypothesis is rejected.

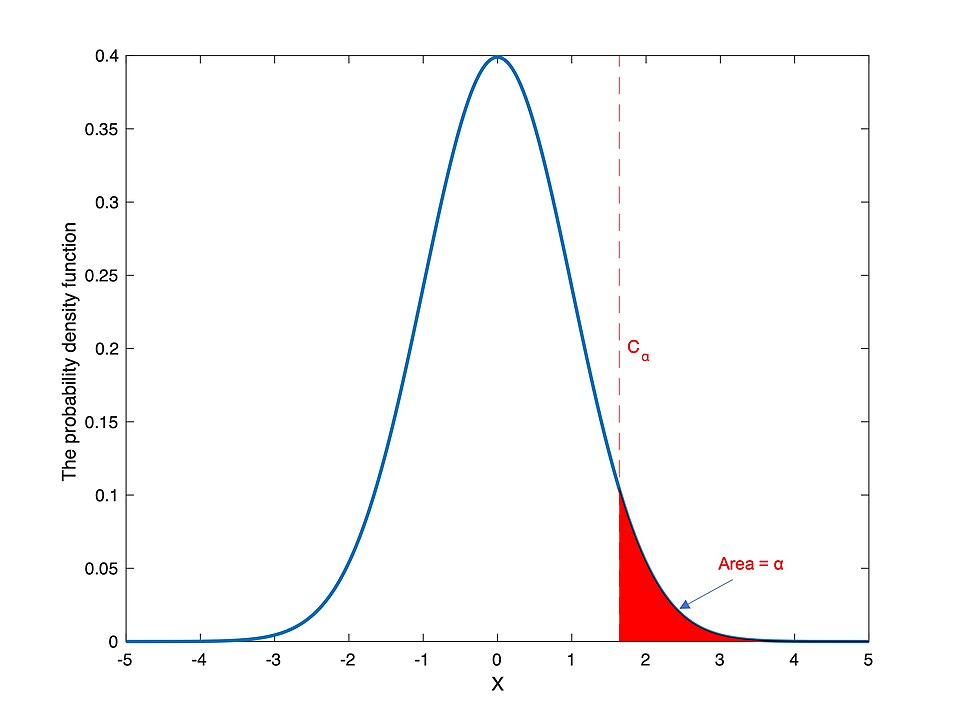
The figure shows a standard normal curve with a right-tail rejection region whose area equals α. The vertical boundary indicates the critical value used to decide whether to reject the null hypothesis. The unshaded portion represents the non-rejection region. Source.

If the p-value exceeds α, the data do not provide strong enough evidence to reject the null hypothesis. This process ensures that α consistently governs the strength of evidence required to challenge the status quo assumption.

Choosing an Appropriate Value for α

While 0.05 is commonly used, the choice of α depends on the context of the study and the consequences associated with a Type I error. Researchers must weigh the risks of an incorrect rejection carefully. Several factors influence the selection of α:

• Severity of consequences
  Higher stakes typically require a smaller α to minimize the probability of incorrect rejection.

• Field-specific standards
  Disciplines with strict evidentiary requirements, such as medicine, often adopt α = 0.01 or smaller.

• Exploratory versus confirmatory analysis
  Exploratory studies may tolerate a larger α, while confirmatory research demands stricter thresholds.

Because α reflects risk tolerance, clarity about its selection strengthens both the design and interpretation of statistical tests.

Why α Must Be Set Before Data Analysis

Fixing α in advance prevents results from influencing decisions about acceptable risk. Changing α after seeing data introduces bias and undermines the validity of statistical inference. Pre-specifying α ensures that the decision rule remains transparent and replicable, which is essential for sound scientific reasoning.

α and the Logic of Evidence in Hypothesis Testing

Significance tests rely on comparing observed outcomes to what would be expected if the null hypothesis were true. The significance level establishes how extreme an outcome must be before it is judged unlikely enough to contradict the null hypothesis. In this way, α helps transform sample evidence into a structured decision by defining the threshold for “unlikely under the null.”

Researchers use α not to measure the probability that the null hypothesis is true, but to control the long-run proportion of incorrect rejections across repeated testing. This perspective emphasizes that α applies to the procedure, not to any single decision.

The Relationship Between α and Scientific Judgment

Choosing and applying α requires interpreting statistical evidence within the research context. The significance level explicitly quantifies the risk accepted in making inferential decisions, helping researchers articulate the strength and limitations of their conclusions. As a result, α serves both a mathematical and conceptual role in guiding how evidence informs claims about population parameters.

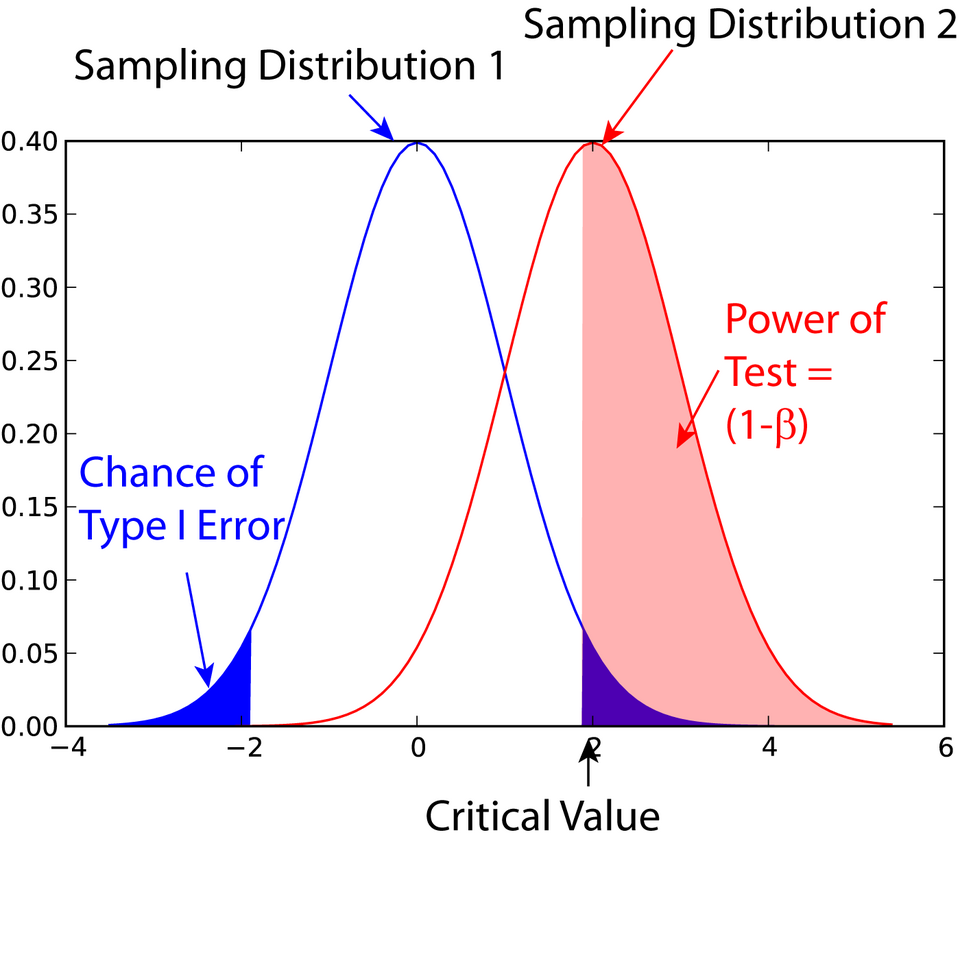
This diagram illustrates the probability of a Type I error as the small shaded tail under the null distribution. It also displays the power of the test under an alternative distribution, showing how α connects to broader inferential error structures. Some additional concepts in the image extend beyond this subsubtopic but visually reinforce the meaning of α. Source.