Independence checks ensure that sample observations do not meaningfully influence each other, protecting the validity of a one-sample z-interval for a population proportion and supporting reliable inference.

Checking for Independence

Establishing independence is essential because inference procedures for proportions assume that each observation in a sample behaves independently of the others. When this assumption holds, the sampling distribution of the sample proportion is more predictable and aligns with the theoretical properties required for constructing confidence intervals.

Why Independence Matters

Statistical methods such as confidence intervals rely on the idea that the outcomes we observe are not systematically connected. If observations influence one another, the sample proportion may not accurately reflect the population proportion. This would undermine the validity of the method and create misleading estimates.

Random Sampling and Randomized Experiments

The syllabus highlights that independence is primarily justified through random sampling or randomized experiments, both of which limit systematic bias and dependence.

Random sampling strengthens independence because the selection of one individual does not alter the probability of selecting another.

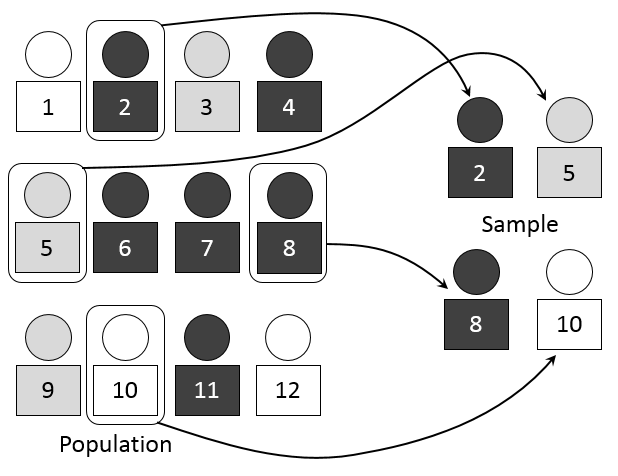
A visual representation of simple random sampling in which each individual has an equal chance of selection, reinforcing the independence assumption for inference. The variety of colors represents different types of individuals but adds no extra statistical content beyond illustrating population diversity. Source.

This process supports a representative sample and aligns with the assumptions required for inference.

Randomized experiments enforce independence across treatment groups by eliminating systematic differences with respect to assignment.

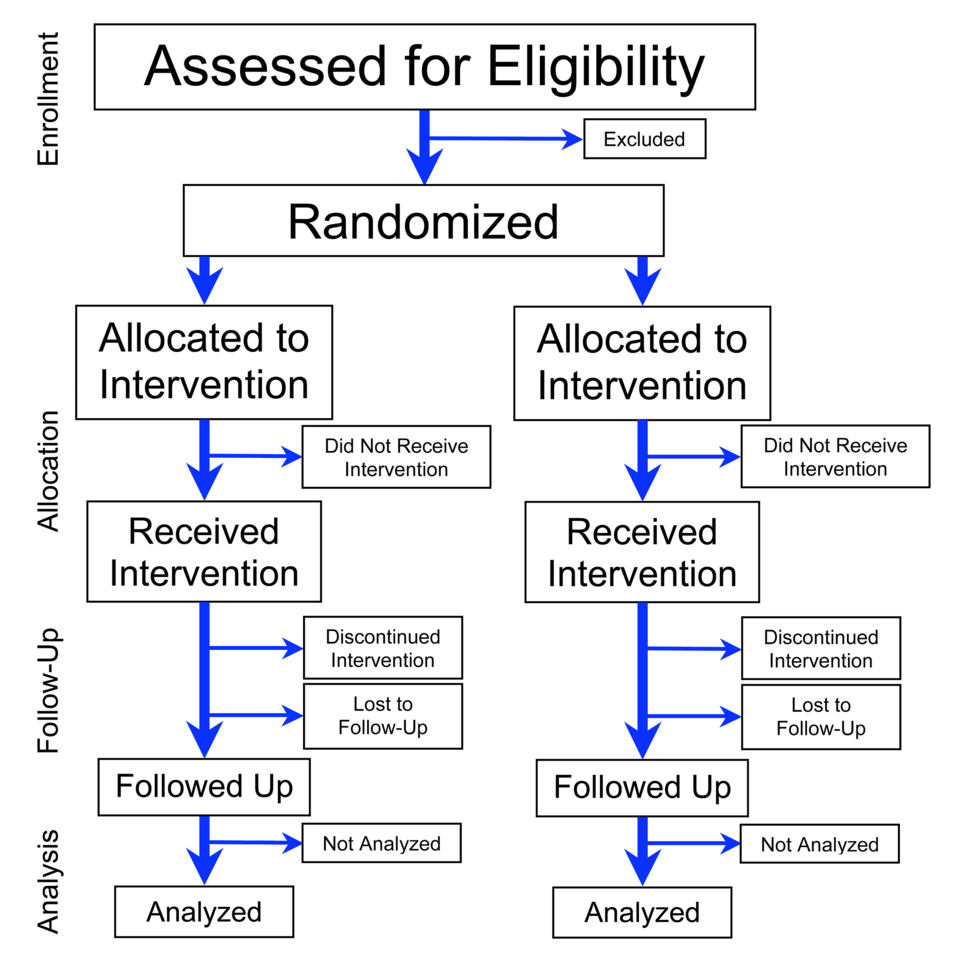
A structured flowchart illustrating the phases of a randomized controlled trial, highlighting the random assignment step that ensures independent treatment groups. Additional elements such as follow-up and analysis reflect real experimental designs but extend slightly beyond AP requirements. Source.

The Role of the 10% Condition

When sampling without replacement, selecting one individual slightly changes the composition of the remaining population. This introduces dependence, but when the sample is small relative to the population, the effect is negligible.

The syllabus emphasizes confirming that the sample size is no more than 10% of the population, often called the 10% condition. This guideline ensures that the dependence introduced through sampling without replacement is too minor to compromise the assumptions of the method.

Although the 10% condition is not itself a formula, it acts as a practical rule to check whether the independence assumption remains reasonable in real-world sampling contexts.

Applying the Independence Checks

In practice, determining independence requires attention to how the data were collected rather than focusing on numerical computations. The following points outline how the student should evaluate independence:

• Confirm random sampling:

  • Was the sample drawn using a method that gives all individuals an equal chance of selection?

  • Does the sampling plan avoid systematic inclusion or exclusion?

• Verify randomized assignment when relevant:

  • If the study compares groups, were participants randomly assigned to conditions?

  • Does the design prevent confounding by balancing unobserved characteristics?

• Evaluate sampling without replacement:

  • If the population is finite and sampling occurs without replacement, check the size relationship between sample and population.

  • Ensure $n \le 0.10N$ to maintain approximate independence.

Even when data arise from well-planned studies, independence must be documented explicitly, as inference procedures require justification grounded in study design rather than assumptions.

Independence in Context

The independence condition does not rely on the value of the sample proportion or uncertainty measures. Instead, it depends solely on how the sample was obtained. This distinguishes independence checks from normality checks and margin-of-error calculations, which rely on sample values.

Independence also situates the confidence interval in its proper context by linking the quality of the estimate to the integrity of the underlying data. Without independent observations, even large samples may produce distorted sample proportions.

Clarifying Common Misunderstandings

Students often mistake independence for a property of numerical results, but it is a property of design. A sample proportion that “looks reasonable” is not evidence of independence; only random sampling or randomized assignment can support that assumption.

Another frequent misunderstanding is believing that large sample sizes automatically ensure independence. In fact, large nonrandom samples can magnify systematic bias, making independence even less plausible.

Relationship to the Broader Inference Framework

Within the framework of constructing a one-sample z-interval for a population proportion, independence serves as the foundational condition before any mathematical procedure can be applied. While later steps involve checking normality and calculating the standard error, these steps depend on independence being satisfied first.

Independence ensures the sampling distribution of the sample proportion behaves consistently with theoretical expectations. All subsequent inference procedures rely on this stability.

Summary of the Required Checks

For clarity, the independence checks required by the syllabus can be expressed as:

• Random sampling or randomized experiment must be used.

• If sampling without replacement, the sample must represent no more than 10% of the population to minimize dependence.

• Independence must be evaluated based on study design, not statistical output.

Through careful attention to these conditions, students can confidently justify the independence assumption necessary for constructing valid confidence intervals for population proportions.